在機器學習中，當我們使用預先分配好的訓練集訓練好一個模型後，此時我們會使用預先分配好的測試集來檢測我們訓練好的這個模型怎麼樣？評價模型好壞的指標有很多，具體可以參見我以前的一篇部落格： 如何理解誤識率（FAR）拒識率（FRR），TPR,FPR以及ROC曲線，很常見的一個指標便是ROC曲線，它是在不同閾值的前提下以fpr以橫座標、tpr為縱座標的二維座標圖。

當我們用測試集去測試模型好壞時，輸出會是一個匹配分數矩陣，那怎麼根據這個匹配分數矩陣來判斷我們的測試集有沒有分對呢，常見的解決方案是我們將這個匹配分數矩陣裡的值從低到高分別設定為閾值，針對每一個閾值，與匹配分數矩陣同樣大小的標籤矩陣對比分別計算此時的tpr以及fpr，最後會得到一組tpr以及fpr值，根據這組tpr以及fpr值就可以畫出ROC曲線，由該ROC曲線就可以判斷我們模型的好壞。

閾值唯一確定之後，那麼我們的模型也就唯一確定了，針對測試集的輸入，fpr以及tpr也唯一確定，為了更好的視覺化我們的分類結果，我們引入混淆矩陣的概念。

在人工智慧中，混淆矩陣（confusion matrix）是視覺化工具，特別用於監督學習，在無監督學習一般叫做匹配矩陣。在影象精度評價中，主要用於比較分類結果和實際測得值，可以把分類結果的精度顯示在一個混淆矩陣裡面。混淆矩陣是通過將每個實測像元的位置和分類與分類影象中的相應位置和分類相比較計算的。

如有150個樣本資料，這些資料分成3類，每類50個。分類結束後得到的混淆矩陣為：

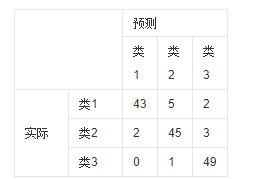
每一行之和為50，表示50個樣本，第一行說明類1的50個樣本有43個分類正確，5個錯分為類2，2個錯分為類3。

混淆矩陣的每一列代表了預測類別，每一列的總數表示預測為該類別的資料的數目；每一行代表了資料的真實歸屬類別，每一行的資料總數表示該類別的資料例項的數目。每一列中的數值表示真實資料被預測為該類的數目：如下圖，第一行第一列中的43表示有43個實際歸屬第一類的例項被預測為第一類，同理，第二行第一列的2表示有2個實際歸屬為第二類的例項被錯誤預測為第一類。

那麼針對以上的混淆矩陣，我們怎樣取計算fpr以及tpr值呢？

針對類1：共有150個測試樣本，類1為50個，那類2和類3就屬於其他樣本共為100個，此時 tpr=TPTP+FN=4343+7=0.86$tpr={\displaystyle \frac{TP}{TP+FN}}={\displaystyle \frac{43}{43+7}}=0.86$ ；fpr

ROC曲線一般針對的是二分類問題，那麼對於我們這裡的3分類問題怎樣畫ROC曲線，採取的策略是針對類1、類2以及類3這3個二分類器，分別計算其在特定閾值下fpr以及tpr的均值即可以畫ROC曲線。