寫在前面的話：

  我現在大四，畢業設計是做一個基於大資料的使用者畫像研究分析。所以開始學習資料探勘的相關技術。這是我學習的一個新技術領域，學習難度比我以往學過的所有技術都難。雖然現在在一家公司實習，但是工作還是挺忙的，經常要加班，無論工作多忙,還是決定要寫一個專欄,這個專欄就寫一些資料探勘演算法、資料結構、演算法設計和分析的相關文章。通過寫博文來督促自己不斷學習。以前對於數學沒有多大的興趣愛好，從小到大，學數學也是為了考試能考個好的成績，學過的很多數學知識，並沒有深刻的感受到它的用途，不用也就慢慢遺忘，但自從我看了數學之美這本書和開始學習資料探勘後，使我對數學有了很大的興趣。數學源於生活，用於生活。資料探勘中涉及到很多統計學、線性代數、微積分等相關知識，而我的很多數學知識都已經還給我以前的老師了，所以現在只能慢慢一點一點撿起來。要感謝網上有很多作者寫出的好的文章，讓我受益匪淺，也算是站在他們的肩膀上學習。減少了我的學習困難，而我今天開始寫的專欄裡的一系列文章，很多例子都是借鑑於他們文章中的例子。想了想，這個專欄名稱就叫<<演算法大雜燴>>

，以後我會把我工作中用到的、自己學習的新演算法、以及回顧梳理的每一個演算法的學習筆記和心得都更新到這個專欄裡。寫的博文難免會有寫得不好的地方，歡迎大家指正,我也喜歡和有共同學習愛好的人一起學習交流。

不一定每天都更會更新，但是肯定會堅持寫下去。

今天寫的第一篇博文，是關於樸素貝葉斯分類的。幾年前，我就聽說過這個演算法，只是稍微瞭解一點點，僅僅停留在只知道它是通過貝葉斯定理來分類的。寫這篇文章之前，我看了很多的相關知識，包括書籍和網上的一些優秀的博文。哈哈，到現在也應該算對於這個演算法入門了吧。後面的參考連結中會附上一些參考的文章地址。

樸素貝葉斯分類

引子

  樸素貝葉斯分類是一種常用的分類演算法，他根據研究物件的某些特徵，來推斷出該研究物件屬於該研究領域的哪個類別。 數學是解決我們生活中產生的各種問題的。所以，數學源於生活，生活中也處處體現數學，我們程式設計，不過是把人能夠理解的數學知識轉換成計算機能夠理解的形式來解決實際問題。拿樸素貝葉斯分類來說，其實生活中比比皆是，舉個例子： 我們在大街上看到一個人，猜測他屬於哪個職業。這就是一種分類，你是根據什麼來判斷的。可能是根據這個人的穿著打扮，言行舉止。 穿著打扮：鬍子拉碴、頭髮亂七八糟，揹著大的電腦包 言行舉止：雙眼無神（估計在想哪個bug的解決辦法），黑眼圈重，頭髮沒洗。 所以，我大概能看出這個人職業是程式設計師（開個玩笑，這只是程式設計師自黑而已，我身邊的程式設計師都不是這樣的，當然也包括我）。 其實穿著打扮、言行舉止就是人的特徵屬性 我們要對某個物件分類，必須根據他的特徵屬性來判斷。

概述

要了解貝葉斯分類，必須瞭解貝葉斯定理，貝葉斯定理離不開條件概率 條件概率定義： 事件A在另外一個事件B已經發生條件下的發生概率。條件概率表示為P（A|B），讀作“在B條件下A的概率”。 根據文氏圖，可以很清楚地看到在事件B發生的情況下，事件A發生的概率就是P(A∩B)除以P(B)。

根據文氏圖，可以很清楚地看到在事件B發生的情況下，事件A發生的概率就是P(A∩B)除以P(B)。

P(A|B)=P(A∩B)/P(B)

因此，

P(A∩B)=P(A|B)P(B)

所以，

P(A|B)P(B)=P(B|A)P(A)

即

P(A|B)=P(B|A)P(A)/P(B)

上面的公式就是貝葉斯定理 生活中，我們經常知道這種情況 ，P(A|B),但是不知道P(B|A).比如： A:   表示使用者收入高 B：表示訂購2G流量套餐 P(A|B) 表示訂購2G流量套餐的使用者收入高的概率，這個可以通過統計的樣本算出得到。 但是現在有一個使用者收入高（A），他購買2G流量套餐(B)的概率是多少，即P(B|A)，這才是我們關注 所以通過貝葉斯定理，我們可以把這兩者掛上鉤，求出我們想知道的P(B|A)

病人疾病預測分類例子

看一個簡單的形式化的列子，來說明貝葉斯分類的作用 這個例子來自：阮一峰老師的介紹貝葉斯應用博文中的一個病人分類的例子 如下：其中特徵屬性是症狀和職業，類別是疾病（包括感冒，過敏、腦震盪） 某個醫院早上收了六個門診病人，如下表。

    症狀　　職業　　　疾病
　　打噴嚏　護士　　　感冒 
　　打噴嚏　農夫　　　過敏 
　　頭痛　　建築工人　腦震盪 
　　頭痛　　建築工人　感冒 
　　打噴嚏　教師　　　感冒 
　　頭痛　　教師　　　腦震盪

現在又來了第七個病人，是一個打噴嚏的建築工人。請問他患上感冒的概率有多大？ 根據貝葉斯定理： 　P(A|B) = P(B|A) P(A) / P(B) 可得

P(感冒|打噴嚏x建築工人) 
　　　　= P(打噴嚏x建築工人|感冒) x P(感冒) 
　　　　/ P(打噴嚏x建築工人)

假定"打噴嚏"和"建築工人"這兩個特徵是獨立的，因此，上面的等式就變成了

P(感冒|打噴嚏x建築工人) 
　　　　= P(打噴嚏|感冒) x P(建築工人|感冒) x P(感冒) 
　　　　/ P(打噴嚏) x P(建築工人)

這是可以計算的。

P(感冒|打噴嚏x建築工人) 
　　　　= 0.66 x 0.33 x 0.5 / 0.5 x 0.33 
　　　　= 0.66

因此，這個打噴嚏的建築工人，有66%的概率是得了感冒。同理，可以計算這個病人患上過敏或腦震盪的概率。比較這幾個概率，就可以知道他最可能得什麼病。 這就是貝葉斯分類器的基本方法：在統計資料的基礎上，依據找到的一些特徵屬性，來計算各個類別的概率，找到概率最大的類，從而實現分類。

貝葉斯分類的定義

1、設為一個待分類項，而每個a為x的一個特徵屬性。

      2、有類別集合。

      3、計算。

      4、求出在X個屬性條件下，所有類別的概率，選取概率最大的。則X屬於概率最大的類別

，則。 

 根據貝葉斯定理，要求P(A|B)，只要求出P(B|A)即可 .這裡Y指A,X指B.把B分解為各個特徵屬性，求出每個類別的每個特徵屬性即可，如下

   1、找到一個已知分類的待分類項集合，這個集合叫做訓練樣本集。   

   2、統計得到在各類別下各個特徵屬性的條件概率估計。即。

   3、如果各個特徵屬性是條件獨立的，則根據貝葉斯定理有如下推導：

      

      因為分母對於所有類別為常數，因為我們只要將分子最大化皆可。又因為各特徵屬性是條件獨立的，所以有：

      

上式等號右邊的每一項，都可以從統計資料中得到，由此就可以計算出每個類別對應的概率，從而找出最大概率的那個類。

注意：各個特徵屬性是條件獨立的，這是樸素貝葉斯所要求的，如果各個特徵屬性不獨立，就不屬於樸素貝葉斯，屬於貝葉斯網路，後面的文章會講解。

賬號真假檢測例子

再看一個例子，該例子來自網上張陽的演算法雜貨鋪博文

根據某社群網站的抽樣統計，該站10000個賬號中有89%為真實賬號（設為C0），11%為虛假賬號（設為C1）。

　　C0 = 0.89

　　C1 = 0.11

接下來，就要用統計資料判斷一個賬號的真實性。假定某一個賬號有以下三個特徵：

　　　　F1: 日誌數量/註冊天數 
　　　　F2: 好友數量/註冊天數 
　　　　F3: 是否使用真實頭像（真實頭像為1，非真實頭像為0）

　　　　F1 = 0.1 
　　　　F2 = 0.2 
　　　　F3 = 0

請問該賬號是真實賬號還是虛假賬號？

方法是使用樸素貝葉斯分類器，計算下面這個計算式的值。

　　　　P(F1|C)P(F2|C)P(F3|C)P(C)

雖然上面這些值可以從統計資料得到，但是這裡有一個問題：F1和F2是連續變數，不適宜按照某個特定值計算概率。

一個技巧是將連續值變為離散值，計算區間的概率。比如將F1分解成[0, 0.05]、(0.05, 0.2)、[0.2, +∞]三個區間，然後計算每個區間的概率。在我們這個例子中，F1等於0.1，落在第二個區間，所以計算的時候，就使用第二個區間的發生概率。

根據統計資料，可得：

　　P(F1|C0) = 0.5, P(F1|C1) = 0.1 
　　P(F2|C0) = 0.7, P(F2|C1) = 0.2 
　　P(F3|C0) = 0.2, P(F3|C1) = 0.9

因此，

　　P(F1|C0) P(F2|C0) P(F3|C0) P(C0) 
　　　　= 0.5 x 0.7 x 0.2 x 0.89 
　　　　= 0.0623

　　P(F1|C1) P(F2|C1) P(F3|C1) P(C1) 
　　　　= 0.1 x 0.2 x 0.9 x 0.11 
　　　　= 0.00198

可以看到，雖然這個使用者沒有使用真實頭像，但是他是真實賬號的概率，比虛假賬號高出30多倍，因此判斷這個賬號為真。

貝葉斯分類的含義

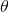
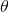
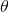
 長久以來，人們對一件事情發生或不發生的概率，只有固定的0和1，即要麼發生，要麼不發生，從來不會去考慮某件事情發生的概率有多大，不發生的概率又是多大。比如如果問那時的人們一個問題：“有一個袋子，裡面裝著若干個白球和黑球，請問從袋子中取得白球的概率是多少？”他們會想都不用想，會立馬告訴你，取出白球的概率就是1/2，要麼取到白球，要麼取不到白球，即θ只能有一個值，不是1/2，就是0，而且不論你取了多少次，取得白球的概率θ始終都是1/2，即不隨觀察結果X 的變化而變化。

直到貝葉斯定理的出現，貝葉斯定理不把概率θ看做一個固定的值（比如上面取白球的概率一直都是1/2），而看做一個隨機變數，他會隨著觀察結果變化

貝葉斯及貝葉斯派提出了一個思考問題的固定模式：

• 先驗分佈 + 樣本資訊  後驗分佈

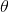
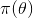
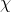
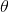
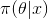
    上述思考模式意味著，新觀察到的樣本資訊將修正人們以前對事物的認知。換言之，在得到新的樣本資訊之前，人們對的認知是先驗分佈，在得到新的樣本資訊後，人們對的認知為。

條件概率公式進行變形，可以得到如下形式：

    P(A|B)=P(A)    *    P(B|A)/P(B)

我們把P(A)稱為"先驗概率"，即在事件B發生之前，事件A發生的概率，在事件B發生之前，它是一個無條件分佈，因為A還沒有與事件B關聯上，他是先驗分佈。

P(A|B)稱為"後驗概率"（Posterior probability），即在B事件發生之後，我們對A事件概率的重新評估。P(B|A)/P(B)稱為"可能性函式"（Likelyhood），這是一個調整因子，使得預估概率更接近真實概率。它的分佈就是後驗分佈

所以，條件概率可以理解成下面的式子：

　　後驗概率　＝　先驗概率 ｘ 調整因子

這就是貝葉斯推斷的含義。我們先預估一個"先驗概率"，然後加入實驗結果，看這個實驗到底是增強還是削弱了"先驗概率"，由此得到更接近事實的"後驗概率"。

在這裡，如果"可能性函式"P(B|A)/P(B)>1，意味著"先驗概率"被增強，事件A的發生的可能性變大；如果"可能性函式"=1，意味著B事件無助於判斷事件A的可能性；如果"可能性函式"<1，意味著"先驗概率"被削弱，事件A的可能性變小。

水果糖問題例子

這個例子同樣來自阮一峰老師的博文，加深對貝葉斯推斷的理解

第一個例子。兩個一模一樣的碗，一號碗有30顆水果糖和10顆巧克力糖，二號碗有水果糖和巧克力糖各20顆。現在隨機選擇一個碗，從中摸出一顆糖，發現是水果糖。請問這顆水果糖來自一號碗的概率有多大？

我們假定，H1表示一號碗，H2表示二號碗。由於這兩個碗是一樣的，所以P(H1)=P(H2)，也就是說，在取出水果糖之前，這兩個碗被選中的概率相同。因此，P(H1)=0.5，我們把這個概率就叫做"先驗概率"，即沒有做實驗之前，來自一號碗的概率是0.5。

再假定，E表示水果糖，所以問題就變成了在已知E的情況下，來自一號碗的概率有多大，即求P(H1|E)。我們把這個概率叫做"後驗概率"，即在E事件發生之後，對P(H1)的修正。

根據貝葉斯定理，得到

P(H1|E)=P(H1)  *  P(E|H1)/P(E)

已知，P(H1)等於0.5，P(E|H1)為一號碗中取出水果糖的概率，等於0.75，那麼求出P(E)就可以得到答案。根據全概率公式（不懂全概率公式的可以查詢相關資料理解），

P(E)=P(E|H1) * P(H1)  +  P(E|H2)*P(H2)

所以，將數字代入原方程，得到

P(H1|E)=0.5*   0.75/0.625=0.6

這表明，來自一號碗的概率是0.6。也就是說，取出水果糖之後，H1事件的可能性得到了增強。

連續型特徵屬性和零概率事件處理

上面講的特徵屬性值，都是離散的，賬號真假檢測例子中把連續的轉換成區間，每個區間也可以看成離散的，但是如果在不能這樣轉換的情況下怎麼解決？如果特徵屬性值是不是離散的，而是連續的怎麼辦？

我們是站在巨人的肩膀上，前人早已經為我們找到了應對之策

當特徵屬性為連續值時，通常假定其值服從高斯分佈（也稱正態分佈）。即：

      

      而

      因此只要計算出訓練樣本中各個類別中此特徵項劃分的各均值和標準差，代入上述公式即可得到需要的估計值。（ak為觀察到的屬性值）

      另一個需要討論的問題就是當P(a|y)=0怎麼辦，當某個類別下某個特徵項劃分沒有出現時，就是產生這種現象，這會令分類器質量大大降低。為了解決這個問題，引入了拉普拉斯校準，它的思想非常簡單，就是對沒類別下所有劃分（概率為零的）的計數加1，這樣如果訓練樣本集數量充分大時，並不會對結果產生影響，並且解決了上述頻率為零的尷尬局面。

買電腦是否和收入相關的例子

驗證買電腦，是否和收入有關的場景下：

類 buys_computer=yes包含1000個元組，有0個元組income=low  ,990個元組 income=medium,10個元組income=high,這些事件的概率分別是0,    0.990,    0.010.

有概率為0,肯定不行.使用拉普拉斯校準，對每個收入-值對應加1個元組，分別得到如下概率

1/1003=0.001    

991/1003=0.998

11/1003=0.011

這些校準的概率估計與對應的未校準的估計很接近，但是避免了零概率值

性別分類的例子

再看一個阮一峰老師的樸素貝葉斯應用一文中摘自維基百科的例子，關於處理連續變數的另一種方法。

下面是一組人類身體特徵的統計資料。

   性別　　身高（英尺）　體重（磅）　腳掌（英寸）
　　男 　　　 6 　　　　　　180　　　　　12 
　  男 　　　 5.92　　　　　190　　　　　11 
　　男 　　　 5.58　　　　　170　　　　　12 
　　男 　　　 5.92　　　　　165　　　　　10 
　　女 　　　 5 　　　　　　100　　　　　 6 
　　女 　　　 5.5 　　　　　150　　　　　 8 
　　女 　　　 5.42　　　　　130　　　　　 7 
　　女 　　　 5.75　　　　　150　　　　　 9

已知某人身高6英尺、體重130磅，腳掌8英寸，請問該人是男是女？

根據樸素貝葉斯分類器，計算下面這個式子的值。

P(身高|性別) x P(體重|性別) x P(腳掌|性別) x P(性別)

這裡的困難在於，由於身高、體重、腳掌都是連續變數，不能採用離散變數的方法計算概率。而且由於樣本太少，所以也無法分成區間計算。怎麼辦？

這時，可以假設男性和女性的身高、體重、腳掌都是正態分佈，通過樣本計算出均值和方差，也就是得到正態分佈的密度函式。有了密度函式，就可以把值代入，算出某一點的密度函式的值。

比如，男性的身高是均值5.855、方差0.035的正態分佈。所以，男性的身高為6英尺的概率的相對值等於1.5789（大於1並沒有關係，因為這裡是密度函式的值，只用來反映各個值的相對可能性）。

有了這些資料以後，就可以計算性別的分類了。

　　P(身高=6|男) x P(體重=130|男) x P(腳掌=8|男) x P(男) 
　　　　= 6.1984 x e-9

　　P(身高=6|女) x P(體重=130|女) x P(腳掌=8|女) x P(女) 
　　　　= 5.3778 x e-4

可以看到，女性的概率比男性要高出將近10000倍，所以判斷該人為女性。

下一篇會寫貝葉斯網路。

參考文章：

http://www.ruanyifeng.com/blog/2011/08/bayesian_inference_part_one.html

http://www.ruanyifeng.com/blog/2013/12/naive_bayes_classifier.html

http://www.cnblogs.com/leoo2sk/archive/2010/09/17/naive-bayesian-classifier.html

http://blog.csdn.net/zdy0_2004/article/details/41096141

參考書籍：資料探勘概念與技術。資料探勘十大演算法，統計學概率論方面的數學知識

碼字不易，轉載請指明出自http://blog.csdn.net/tanggao1314/article/details/66478782