KMP演算法及next陣列詳解
事實上這三種“next陣列”的結果都沒有錯,只是他們涉及到了KMP匹配過程的兩種理解。在後文中將說明這三者之間的區別、轉換以及所屬的KMP匹配過程的演示。
第一部分 KMP演算法與next陣列的基本認識
設主串為T,帶搜尋的子串為S,i表示T遍歷到了哪個字元,j表示S遍歷到了哪個字元:
暴力查詢方法通常會在T[i]!=S[j]時,j和j都回退,而KMP的核心就是主串不回退,即i只增不減,j相應的改變。而j依何改變?這就需要提前處理T子串,生成相應的next陣列(這裡所說的next陣列其實並不完善,後文中將會提到改良版的nextval陣列)。
那麼next陣列代表的是什麼意思呢?通俗點說就是,這次沒配上,下次找誰配。next數組裡存的就是下次交配物件...不對,是匹配物件...
正是因為KMP只預處理子串,因此很適合這樣一種問題的求解:給定一個S子串,和一群不同的T主串,問S是哪些T的子串。
第二部分 KMP演算法的兩種匹配過程
同我一樣迷惑於許多部落格中講述的“互相矛盾的”匹配過程的童鞋請重點看這一部分,接下來我將說明,為何明明很好理解的主串不回退匹配過程會有那麼多不同的聲音,因為它們根..本..不..是..一..個..過..程..!!!
這也是為什麼關於next陣列會有那麼多版本的不同解釋,先約束下,本文中用到的陣列以1開始(以0開始也一樣整體減1就好了,網上next陣列第一位為-1的就是陣列以0開始的)。
下表中Lmax代表失配字元上一位字元所對應部分子串的最大前後綴共有元素長度,也就是部分匹配值,next代表存在一些瑕疵的next陣列,nextval代表改良版的next陣列。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| S | a | b | a | a | b | c | a | c |
| Lmax | 0 | 0 | 1 | 1 | 2 | 0 | 1 | 0 |
| next | 0 | 1 | 1 | 2 | 2 | 3 | 1 | 2 |
| nextval | 0 | 1 | 0 | 2 | 1 | 3 | 0 | 2 |
1.部分匹配值法
推薦部落格:http://www.ruanyifeng.com/blog/2013/05/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm.html 詳細且圖文並茂(只可惜沒有next陣列什麼事),能夠幫助大家快速理解KMP到底要幹什麼。
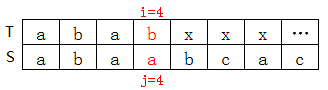

注意,這裡只是單純的S子串向後移動兩位,不涉及j變化成什麼(可以推出j變為什麼,但是不是Lmax直接賦值給j) 2.next陣列法
推薦部落格:http://blog.csdn.net/guo_love_peng/article/details/6618170 寫的真心好,這個才是KMP演算法中正宗的next陣列。 同樣是上圖中的例子,接下來用到的是next/nextval陣列法: (1)next/nextval通用例子:

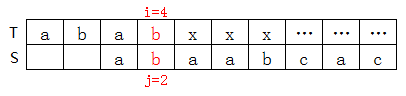
T[4]=b,S[4]=a,不匹配,查上表知nextval[4]=2(巧了next[4]也等於2,事實上大多數情況下二者都相等),因此j=nextval[4]=2,如下圖:
(2)證明next有瑕疵,nextval完美的例子
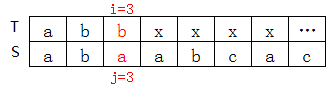
T[3]=b,S[3]=a,不匹配,查上表知nextval[3]=0(next[3]也等於1,不相等)
先看next[3]=1的情況:
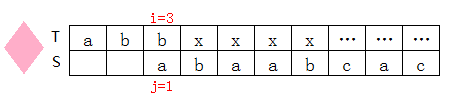
T[3]=b,S[1]=a,不匹配,查上表知next[1]=0,則j=next[1]=0:
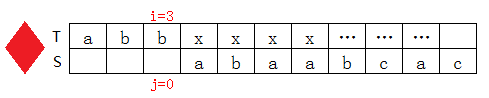
i++,j++,繼續匹配:
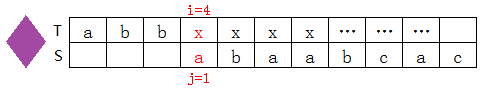
接下來是nextval[3]=0的情況:

next[3]=1需要經過步驟
 ,而nextval[3]=0只要一步
,而nextval[3]=0只要一步 就搞定,為什麼呢?
就搞定,為什麼呢?其實,既然T[3]=b不等於S[3]=a,而S[3]=S[1]=a,那麼T[3]=b就一定不等於S[1]=a,既然如此,那麼步驟
 就多此一舉了,這也就是next的瑕疵之所在,而nextval是在next基礎上的一個改良版,避免了不必要的匹配過程。
第三部分 Lmax、next、nextval陣列的獲取方法及轉換
就多此一舉了,這也就是next的瑕疵之所在,而nextval是在next基礎上的一個改良版,避免了不必要的匹配過程。
第三部分 Lmax、next、nextval陣列的獲取方法及轉換1.最大共有元素長度(部分匹配值)Lmax
//虛擬碼如下
Lmax[1]=0;
j=0;
for i=2 to n do{
while j>0 and S[j+1]!=S[i]
do j=Lmax<span style="font-size: 12px; font-family: Arial, Helvetica, sans-serif;">[j];</span>
if S[j+1]=S[j]
then j++;
Lmax[i]=j;
}獲取方法:
(1)next[1]=0,next[2]=1 (固定)
(2)之後的每一位next值根據上一位進行比較,前一位值與其next值對應的內容相比較:
a.如果相等,則該位的next值就是前一位的next值加上1
b.如果不相等,向前繼續找next值對應的內容與前一位進行比較,知道找到某一位內容的next值對應的內容與前一位相等,則此next值加上1即為該位的next值
c.如果找到第一位都沒有與前一位相等的內容,那麼該位next值為1
3.nextval陣列(改良後的next)
//虛擬碼如下
i=1;
j=0;
nextval[1]=0;
while i<S[0]{
whlie j>0 and S[i]!=S[j]
do j=nextval[j];
i++;
j++;
if S[i]=S[j]
then nextval[i]=nextval[j];
else
then nextval[i]=j;
}4.最大共有元素長度Lmax,next,nextval陣列之間的轉換 (1)Lmax->next: 右移一位,最左補-1,最右刪去,整體加1
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| S | a | b | a | a | b | c | a | c |
| Lmax | 0 | 0 | 1 | 1 | 2 | 0 | 1 | 0 |
| next | 0 | 1 | 1 | 2 | 2 | 3 | 1 | 2 |
| nextval | 0 | 1 | 0 | 2 | 1 | 3 | 0 | 2 |
(2)next->nextval:
<1>nextval[1]=0 (固定)
<2>從第二位開始(i=2),若要求nextval[i],將next[i]的值對應位的值與i的值進行比較:
a.若相等,則nextval[i]=nextval[next[i]]
b.若不相等,則nextval[i]=next[i]
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| S | a | b | a | a | b | c | a | c |
| Lmax | 0 | 0 | 1 | 1 | 2 | 0 | 1 | 0 |
| next | 0 | 1 | 1 | 2 | 2 | 3 | 1 | 2 |
| nextval | 0 | 1 | 0 | 2 | 1 | 3 | 0 | 2 |
相關推薦
KMP演算法及next陣列詳解
最近整理筆記時,突然翻出幾年前理解起來困難無比的看毛片(KMP)演算法,筆記中詳述了搜尋過程,圖文並茂,然而在最最重要的next陣列部分卻是一帶而過,於是找出當年的教材,也只是寫了getnext()函式,想著上網找一找圖文並茂的舉例,結果這一找徹底蒙比,眾說紛紜,同
KMP演算法--Next陣列詳解與優化
本篇文章直接跳過蠻力演算法以及一些簡單背景,著重討論Next陣列的意義以及其是如何工作的,並對如何求Next陣列做詳細記錄。 1.背景 1.1 KMP演算法的應用:KMP演算法用來解決模式串匹配問題。 1.2 為什麼要用KMP演算法:普通的蠻力演算法時間複雜度為O(n*
OHEM演算法及Caffe程式碼詳解
版權宣告:本文為博主原創文章,未經博主允許不得轉載。 https://blog.csdn.net/u014380165/article/details/73148073 這是CVPR2016的一篇論文,用於目標檢測,本篇博文先介紹這個演算法,然後介紹其Caffe程
kmp演算法 關於next陣列的詳細解釋
前言 之前對kmp演算法雖然瞭解它的原理,即求出P0···Pi的最大相同前後綴長度k;但是問題在於如何求出這個最大前後綴長度呢?我覺得網上很多帖子都說的不是很清楚,總感覺沒有把那層紙戳破,後來翻看演算法導論,32章 字串匹配雖然講到了對前後綴計算的正確性,但
KMP演算法、next陣列與字首中的週期(相關題目:Power strings, poj2406)
在一個大的字串S中查詢字串T,naive的演算法時間複雜度為O(s * t)(這裡s與t代表S的長度與T的長度);而應用KMP,時間複雜度為O(s + t)。 KMP演算法的核心在於next陣列。next陣列只與字串T有關,與S無關。 next陣列的核心思想是儲存字串T
JVM 垃圾回收演算法及回收器詳解
本文主要講述JVM中幾種常見的垃圾回收演算法和相關的垃圾回收器,以及常見的和GC相關的效能調優引數。 GC Roots 我們先來了解一下在Java中是如何判斷一個物件的生死的,有些語言比如Python是採用引用計數來統計的,但是這種做法可能會遇見迴圈引用的問題,在Java以及C#
KMP演算法中next陣列、nextval陣列的手工計算
剛接觸資料結構,對於其中的一些演算法都不是很瞭解,這幾天剛在學習串的內容,裡面介紹了兩種串的模式匹配演算法,一種是BF演算法(也叫做BoyFriend演算法);另一種是KMP演算法(也叫做“看毛片”演算法)。BF演算法的實現很簡單,很暴力,但是在時間複雜度的限制下,這不是一個
SSD(single shot multibox detector)演算法及Caffe程式碼詳解
這篇部落格主要介紹SSD演算法,該演算法是最近一年比較優秀的object detection演算法,主要特點在於採用了特徵融合。 演算法概述: 本文提出的SSD演算法是一種直接預測bounding box的座標和類別的object detection
關於KMP演算法中next陣列和nextVal陣列求法的整理
例如: 序號 1 2 3 4 5 6 7 8 模式串 a b a a b c a c next值 0 1 1 2 2 3 1 2 next陣列的求解方法是: 第一位的next值為0,第二位的next值為1,後面求解每一位的next值時,根據前一位進行比較。
R-FCN演算法及Caffe程式碼詳解
本篇部落格一方面介紹R-FCN演算法(NISP2016文章),該演算法改進了Faster RCNN,另一方面介紹其Caffe程式碼,這樣對演算法的認識會更加深入。 要解決的問題: 這篇論文提出一種基於region的object detection演算
最簡單的KMP演算法求next陣列值的方法
本文依照嚴蔚敏串的資料結構(C語言版本)總結的方法: next陣列的求解方法是: 注意:1. j的下標識從0開始排的 2. 規定next[0]=-1,next[1]=0 j
字串匹配KMP演算法中Next[]陣列求法
int get_nextval(SString T,int &nextval[ ]){ //求模式串T的next函式修正值並存入陣列nextval。 i=1; nextval[1]=0; j=0; while(i<T[0]){
SSD(single shot multibox detector)演算法及Caffe程式碼詳解(轉載)
這篇部落格主要介紹SSD演算法,該演算法是最近一年比較優秀的object detection演算法,主要特點在於採用了特徵融合。 演算法概述: 本文提出的SSD演算法是一種直接預測bounding box的座標和類別的object detection演算法,沒有生
KMP演算法中next陣列的手工計算方法
筆試題目中經常要求計算KMP演算法的next陣列,網上有很多討論的文章,但是感覺都講的不太清楚,特別是在如何手工計算這一方面,所以今天特別整理了一下放到這裡,一來備忘,二來也希望給有緣人帶來一些方便。 位置編號 1 2 3 4 5
關於kmp演算法中next陣列的求法【針對手算的】
關於kmp演算法中next陣列的求法【手算版本】 本篇只介紹next的求法和nextval的求法 例如 模式串:a b c d c a b c d s a c next
KMP演算法之Next和Nextval詳解
KMP演算法是模式匹配專用演算法 它是在已知模式串的next或nextval陣列的基礎上執行的。如果不知道它們二者之一,就沒法使用KMP演算法,因此我們需要計算它們。 KMP演算法由兩部分組成: 第一部分,計算模式串的next或nextval陣列。 第二
Spark MLlib 貝葉斯分類演算法例項具體程式碼及執行過程詳解
import org.apache.log4j.{Level, Logger} import org.apache.spark.{SparkConf, SparkContext} import org.apache.spark.mllib.classification.{NaiveBayes, Naiv
KMP及next陣列實現程式碼
next陣列求解: 以1開始,next[1]=0,next[2]=1,next[n] :將前面n-1個字元,計算從首尾開始組成最大的相同子串的長度,如果找到,那麼next值是該長度加1,否則next值是1。 void getNext(char *p,in
KMP演算法中next和nextval陣列的計算方法
設字串S=’aabaabaabaac’P=’aabaac’ 1.給出S和P的next值和nextvai值; 2.若S作主串,P為模式串,試給出利用BF演算法和KMP演算法的匹配過程. 答:1.給出S和P的next值和nextvai值; 失效函式採用的是清華殷人昆的資料結構上的
KMP演算法的next、next value陣列的手工計算
昨天下午在書上看到了KMP演算法,看了很多很多很多遍都搞不懂什麼邏輯和原理;今天上午又聽了學長講了一遍感覺沒大聽懂,自己又上網找了很多相關文章,試了很多例子,終於找出來KMP演算法中手工計算
