前言

CNN

cnn每一層會輸出多個feature map, 每個feature map由多個神經元組成，假如某個feature map的shape是m*n, 則該feature map有m*n個神經元

卷積層

卷積計算

設當前層l為卷積層，下一層l+1為子取樣層subsampling.
則卷積層l的輸出feature map為：
Xlj=f(∑i∈MjXl−1i∗klij+blj)
∗為卷積符號

殘差計算

設當前層l為卷積層，下一層l+1為子取樣層subsampling.
第l層的第j個feature map的殘差公式為:

δlj=βl+1j(f

′(μlj)∘up(δl+1j))(1)

其中
f(x)=11+e−x(2),
其導數

f′(x)=f(x)∗(1−f(x))(3)

為了之後的推導，先提前講講subsample過程，比較簡單，假設取樣層是對卷積層的均值處理，如卷積層的輸出feature map(f(μlj))是
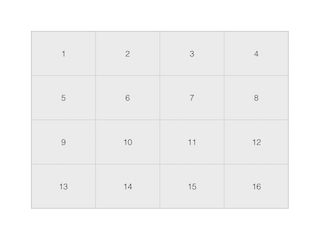
卷積層的feature map

則經過subsample的結果是:
子抽樣層的feature map

subsample過程如下:

import java.util.Arrays;

/**
 * Created by keliz on 7/7/16.
 */

public class test
{
    /**
     * 卷積核或者取樣層scale的大小,長與寬可以不等.
     */ 

    public static class Size
    {

        public final int x;
        public final int y;

        public Size(int x, int y)
        {
            this.x = x;
            this.y = y;
        }

    }

    /**
     * 對矩陣進行均值縮小
     *
     * @param matrix
     * @param scale
     * @return
     */
    public 
 static double[][] scaleMatrix(final double[][] matrix, final Size scale)
    {
        int m = matrix.length;
        int n = matrix[0].length;
        final int sm = m / scale.x;
        final int sn = n / scale.y;
        final double[][] outMatrix = new double[sm][sn];
        if (sm * scale.x != m || sn * scale.y != n)
            throw new RuntimeException("scale不能整除matrix");
        final int size = scale.x * scale.y;
        for (int i = 0; i < sm; i++)
        {
            for (int j = 0; j < sn; j++)
            {
                double sum = 0.0;
                for (int si = i * scale.x; si < (i + 1) * scale.x; si++)
                {
                    for (int sj = j * scale.y; sj < (j + 1) * scale.y; sj++)
                    {
                        sum += matrix[si][sj];
                    }
                }
                outMatrix[i][j] = sum / size;
            }
        }
        return outMatrix;
    }

    public static void main(String args[])
    {
        int row = 4;
        int column = 4;
        int k = 0;
        double[][] matrix = new double[row][column];
        Size s = new Size(2, 2);
        for (int i = 0; i < row; ++i)
            for (int j = 0; j < column; ++j)
                matrix[i][j] = ++k;
        double[][] result = scaleMatrix(matrix, s);
        System.out.println(Arrays.deepToString(matrix).replaceAll("],", "]," + System.getProperty("line.separator")));

        System.out.println(Arrays.deepToString(result).replaceAll("],", "]," + System.getProperty("line.separator")));
    }
}

其中3.5=(1+2+5+6)/(2*2); 5.5=(3+4+7+8)/(2*2)
由此可知,卷積層輸出的feature map中的值為1的節點,值為2的節點,值為5的節點,值為6的節點（神經元）與subsample層的值為3.5的節點相連線，值為3,值為4,值為7,值為8節點與subsample層的值為5.5節點相連線。由BP演算法章節的推導結論可知

卷積層第j個節點的殘差等於子取樣層與其相連線的所有節點的權值乘以相應的殘差的加權和再乘以該節點的導數

對著公式看比較容易理解這句話。
假設子取樣層的對應文中的卷積層的殘差δl+1j是，
子取樣層的delta
按照公式(1),節點1值為0.5的殘差是

βl+1j(f′(1)∗δl+1j(3.5))(4)
因為這是計算單個神經元的殘差，所以需要把∘換成∗, ∘這個運算子代表矩陣的點乘即對應元素相乘，而且節點(神經元)1的對應子取樣層的值為3.5的節點, 由公式(3),可知節點1的殘差是
f(1)∗(1−f(1))∗δl+1j(3.5)
即
11+e−1∗e−11+e−1∗0.5
同理，對於節點2,
殘差為
f(2)∗(1−f(2))∗δl+1j(3.5)
對於節點5,
殘差為
f(5)∗(1−f(5))∗δl+1j(3.5)
對於節點6,
殘差為
f(6)∗(1−f(6))∗δl+1j(3.5)
因為節點3對應的子取樣層的殘差是0.6,所以節點3的殘差為
f(3)∗(1−f(3))∗δl+1j(5.5)
即
11+e−5∗e

CNN 卷積神經網路-- 殘差計算

前言

CNN

卷積層

卷積計算

殘差計算

CNN 卷積神經網路-- 殘差計算

詳細解釋CNN卷積神經網路各層的引數和連線個數的計算

詳細解釋CNN卷積神經網路各層的引數和連結個數的計算

Keras學習（四）——CNN卷積神經網路

CNN卷積神經網路簡單實現模型

【深度學習】Tensorflow——CNN 卷積神經網路 2

【深度學習】Tensorflow——CNN 卷積神經網路 1

TensorFlow之CNN卷積神經網路的實現

DeepLearning tutorial（4）CNN卷積神經網路原理簡介+程式碼詳解

Python CNN卷積神經網路程式碼實現

TensorFlow實現CNN卷積神經網路對手寫數字集mnist的模型訓練

CNN卷積神經網路入門整合

CNN-卷積神經網路

吳恩達deeplearning之CNN—卷積神經網路入門

CNN卷積神經網路原理的直觀理解

CNN卷積神經網路

python神經網路案例——CNN卷積神經網路實現mnist手寫體識別

CNN卷積神經網路基礎

CNN卷積神經網路學習筆記1：背景介紹

用keras小試CNN卷積神經網路應用於人臉識別

CNN 卷積神經網路-- 殘差計算

前言

CNN

卷積層

卷積計算

殘差計算

相關推薦