傅立葉變化,短時傅立葉分析,小波變換
下面我就按照傅立葉-->短時傅立葉變換-->小波變換的順序,講一下為什麼會出現小波這個東西、小波究竟是怎樣的思路。(反正題主要求的是通俗形象,沒說簡短,希望不會太長不看。。)
一、傅立葉變換
關於傅立葉變換的基本概念在此我就不再贅述了,預設大家現在正處在理解了傅立葉但還沒理解小波的道路上。(在第三節小波變換的地方我會再形象地講一下傅立葉變換)
下面我們主要將傅立葉變換的不足。即我們知道傅立葉變化可以分析訊號的頻譜,那麼為什麼還要提出小波變換?答案就是方沁園所說的,“對非平穩過程,傅立葉變換有侷限性”。看如下一個簡單的訊號:<img src="https://pic1.zhimg.com/da6c4b8ce1672d4997000eb08444824c_b.jpg" data-rawwidth="597" data-rawheight="284" class="origin_image zh-lightbox-thumb" width="597" data-original="https://pic1.zhimg.com/da6c4b8ce1672d4997000eb08444824c_r.jpg">做完FFT(快速傅立葉變換)後,可以在頻譜上看到清晰的四條線,訊號包含四個頻率成分。
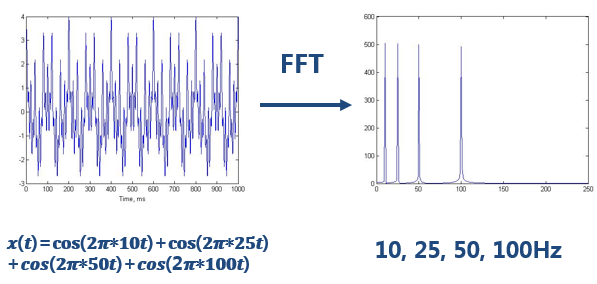
一切沒有問題。但是,如果是頻率隨著時間變化的非平穩訊號呢?
<img src="https://pic1.zhimg.com/def600cea95fa10e3872e88dc8059d6c_b.jpg" data-rawwidth="690" data-rawheight="612" class="origin_image zh-lightbox-thumb" width="690" data-original="https://pic1.zhimg.com/def600cea95fa10e3872e88dc8059d6c_r.jpg">
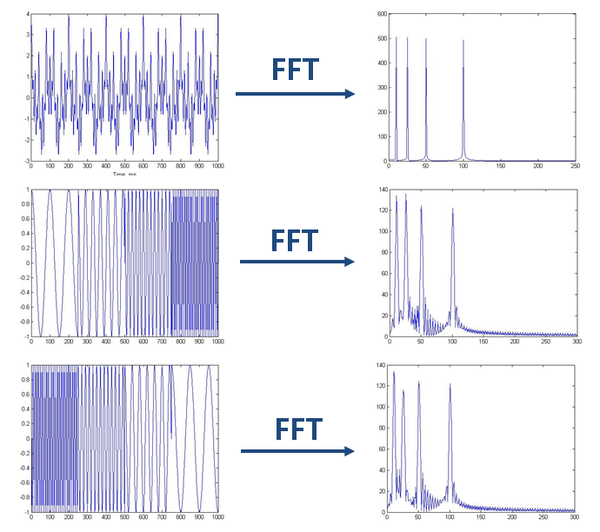
如上圖,最上邊的是頻率始終不變的平穩訊號。而下邊兩個則是頻率隨著時間改變的非平穩訊號,它們同樣包含和最上訊號相同頻率的四個成分。
做FFT後,我們發現這三個時域上有巨大差異的訊號,頻譜(幅值譜)卻非常一致。尤其是下邊兩個非平穩訊號,我們從頻譜上無法區分它們,因為它們包含的四個頻率的訊號的成分確實是一樣的,只是出現的先後順序不同。
可見,傅立葉變換處理非平穩訊號有天生缺陷。它只能獲取一段訊號總體上包含哪些頻率的成分,但是對各成分出現的時刻並無所知。因此時域相差很大的兩個訊號,可能頻譜圖一樣。
然而平穩訊號大多是人為製造出來的,自然界的大量訊號幾乎都是非平穩的,所以在比如生物醫學訊號分析等領域的論文中,基本看不到單純傅立葉變換這樣naive的方法。
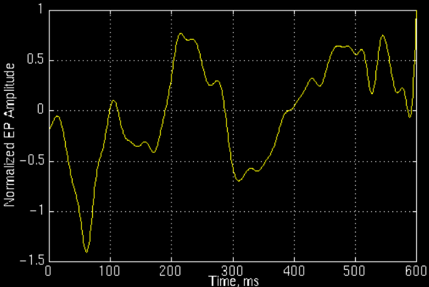
<img src="https://pic3.zhimg.com/e71310fc73e7beba589b76264564abee_b.jpg" data-rawwidth="429" data-rawheight="287" class="origin_image zh-lightbox-thumb" width="429" data-original="https://pic3.zhimg.com/e71310fc73e7beba589b76264564abee_r.jpg">上圖所示的是一個正常人的事件相關電位。對於這樣的非平穩訊號,只知道包含哪些頻率成分是不夠的,我們還想知道
二、短時傅立葉變換(Short-time Fourier Transform, STFT)
一個簡單可行的方法就是——加窗。我又要套用方沁園同學的描述了,“把整個時域過程分解成無數個等長的小過程,每個小過程近似平穩,再傅立葉變換,就知道在哪個時間點上出現了什麼頻率了。”這就是短時傅立葉變換。
看圖:
<img src="https://pic3.zhimg.com/7f4ac3c30283e657406d6661300478a2_b.jpg" data-rawwidth="844" data-rawheight="449" class="origin_image zh-lightbox-thumb" width="844" data-original="https://pic3.zhimg.com/7f4ac3c30283e657406d6661300478a2_r.jpg">時域上分成一段一段做FFT,不就知道頻率成分隨著時間的變化情況了嗎!
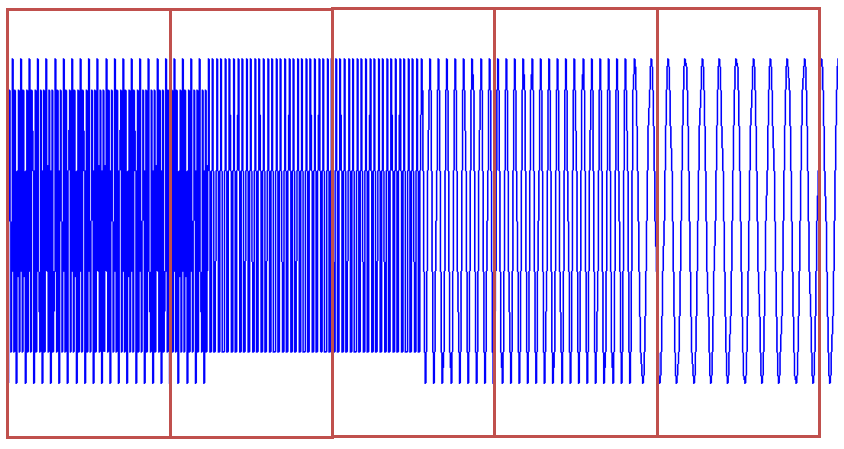 時域上分成一段一段做FFT,不就知道頻率成分隨著時間的變化情況了嗎!
時域上分成一段一段做FFT,不就知道頻率成分隨著時間的變化情況了嗎!用這樣的方法,可以得到一個訊號的時頻圖了:
<img src="https://pic1.zhimg.com/fec492fbcf67ddde4cb6017b62497bf4_b.jpg" data-rawwidth="649" data-rawheight="492" class="origin_image zh-lightbox-thumb" width="649" data-original="https://pic1.zhimg.com/fec492fbcf67ddde4cb6017b62497bf4_r.jpg"> ——此影象來源於“THE WAVELET TUTORIAL”
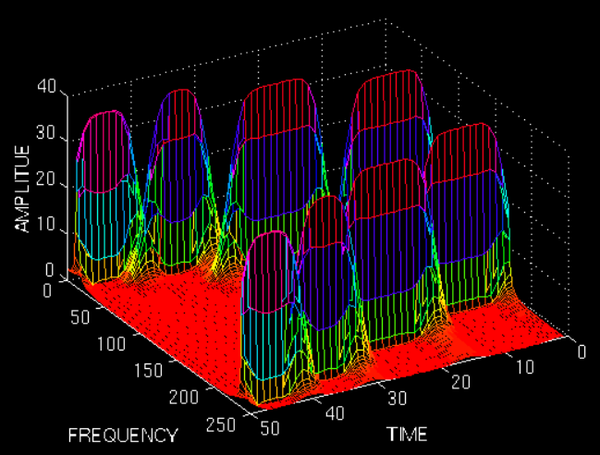 ——此影象來源於“THE WAVELET TUTORIAL”
——此影象來源於“THE WAVELET TUTORIAL”圖上既能看到10Hz, 25 Hz, 50 Hz, 100 Hz四個頻域成分,還能看到出現的時間。兩排峰是對稱的,所以大家只用看一排就行了。
是不是棒棒的?時頻分析結果到手。但是STFT依然有缺陷。
使用STFT存在一個問題,我們應該用多寬的窗函式?
窗太寬太窄都有問題:<img src="https://pic4.zhimg.com/479dd3f809656bf154456868b65e73b3_b.jpg" data-rawwidth="627" data-rawheight="312" class="origin_image zh-lightbox-thumb" width="627" data-original="https://pic4.zhimg.com/479dd3f809656bf154456868b65e73b3_r.jpg">
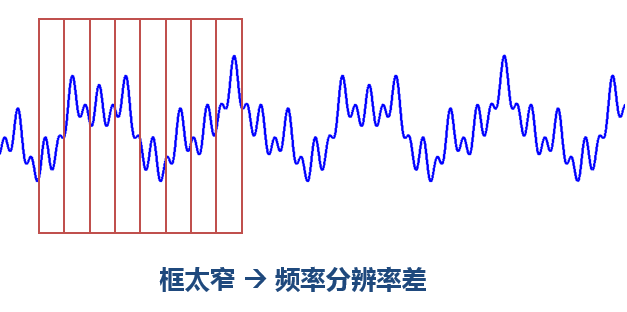
<img src="https://pic3.zhimg.com/9da6c3e9704c32bfb7b53b995532878e_b.jpg" data-rawwidth="609" data-rawheight="350" class="origin_image zh-lightbox-thumb" width="609" data-original="https://pic3.zhimg.com/9da6c3e9704c32bfb7b53b995532878e_r.jpg">窗太窄,窗內的訊號太短,會導致頻率分析不夠精準,頻率解析度差。窗太寬,時域上又不夠精細,時間解析度低。
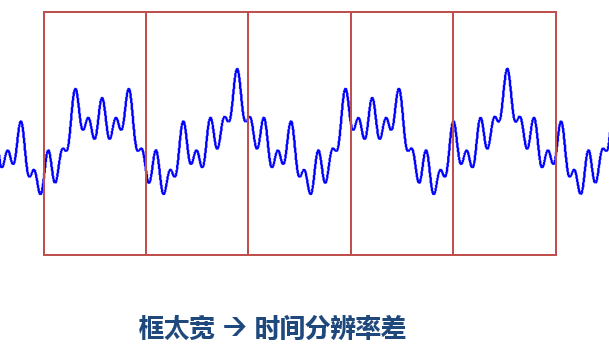 窗太窄,窗內的訊號太短,會導致頻率分析不夠精準,頻率解析度差。窗太寬,時域上又不夠精細,時間解析度低。
窗太窄,窗內的訊號太短,會導致頻率分析不夠精準,頻率解析度差。窗太寬,時域上又不夠精細,時間解析度低。(這裡插一句,這個道理可以用海森堡不確定性原理來解釋。類似於我們不能同時獲取一個粒子的動量和位置,我們也不能同時獲取訊號絕對精準的時刻和頻率。這也是一對不可兼得的矛盾體。我們不知道在某個瞬間哪個頻率分量存在,我們知道的只能是在一個時間段內某個頻帶的分量存在。 所以絕對意義的瞬時頻率是不存在的。)
看看例項效果吧:<img src="https://pic1.zhimg.com/565a3c57d43c8f2f78a5b1dc0de66e34_b.jpg" data-rawwidth="608" data-rawheight="292" class="origin_image zh-lightbox-thumb" width="608" data-original="https://pic1.zhimg.com/565a3c57d43c8f2f78a5b1dc0de66e34_r.jpg">
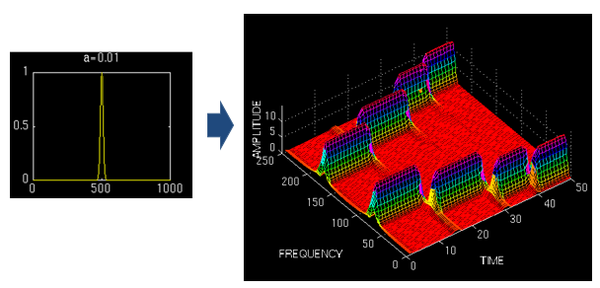
<img src="https://pic3.zhimg.com/c7d2d230a8c4766569c5a77fac901eea_b.jpg" data-rawwidth="604" data-rawheight="295" class="origin_image zh-lightbox-thumb" width="604" data-original="https://pic3.zhimg.com/c7d2d230a8c4766569c5a77fac901eea_r.jpg">
 <img
src="https://pic2.zhimg.com/39822d6589c4486a0a91a148e0a3e571_b.jpg" data-rawwidth="614" data-rawheight="281" class="origin_image zh-lightbox-thumb" width="614" data-original="https://pic2.zhimg.com/39822d6589c4486a0a91a148e0a3e571_r.jpg">
——此影象來源於“THE WAVELET TUTORIAL”
<img
src="https://pic2.zhimg.com/39822d6589c4486a0a91a148e0a3e571_b.jpg" data-rawwidth="614" data-rawheight="281" class="origin_image zh-lightbox-thumb" width="614" data-original="https://pic2.zhimg.com/39822d6589c4486a0a91a148e0a3e571_r.jpg">
——此影象來源於“THE WAVELET TUTORIAL”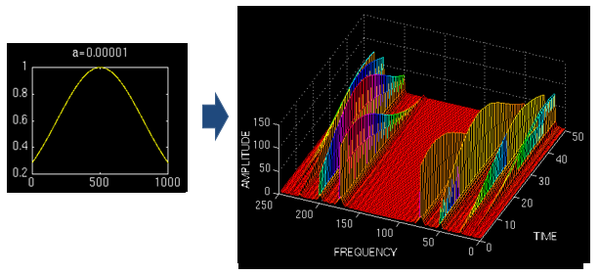 ——此影象來源於“THE WAVELET TUTORIAL”
——此影象來源於“THE WAVELET TUTORIAL”上圖對同一個訊號(4個頻率成分)採用不同寬度的窗做STFT,結果如右圖。用窄窗,時頻圖在時間軸上解析度很高,幾個峰基本成矩形,而用寬窗則變成了綿延的矮山。但是頻率軸上,窄窗明顯不如下邊兩個寬窗精確。
所以窄視窗時間解析度高、頻率解析度低,寬視窗時間解析度低、頻率解析度高。對於時變的非穩態訊號,高頻適合小視窗,低頻適合大視窗。然而STFT的視窗是固定的,在一次STFT中寬度不會變化,所以STFT還是無法滿足非穩態訊號變化的頻率的需求。
三、小波變換
那麼你可能會想到,讓視窗大小變起來,多做幾次STFT不就可以了嗎?!沒錯,小波變換就有著這樣的思路。
但事實上小波並不是這麼做的(關於這一點,方沁園同學的表述“小波變換就是根據演算法,加不等長的窗,對每一小部分進行傅立葉變換”就不準確了。小波變換並沒有採用窗的思想,更沒有做傅立葉變換。)
至於為什麼不採用可變窗的STFT呢,我認為是因為這樣做冗餘會太嚴重,STFT做不到正交化,這也是它的一大缺陷。
於是小波變換的出發點和STFT還是不同的。STFT是給訊號加窗,分段做FFT;而小波直接把傅立葉變換的基給換了——將無限長的三角函式基換成了有限長的會衰減的小波基。這樣不僅能夠獲取頻率,還可以定位到時間了~
【解釋】
來我們再回顧一下傅立葉變換吧,沒弄清傅立葉變換為什麼能得到訊號各個頻率成分的同學也可以再借我的圖理解一下。
傅立葉變換把無限長的三角函式作為基函式:
<img src="https://pic4.zhimg.com/be914c25f4886601caf2324b855b2b9f_b.jpg" data-rawwidth="732" data-rawheight="504" class="origin_image zh-lightbox-thumb" width="732" data-original="https://pic4.zhimg.com/be914c25f4886601caf2324b855b2b9f_r.jpg">
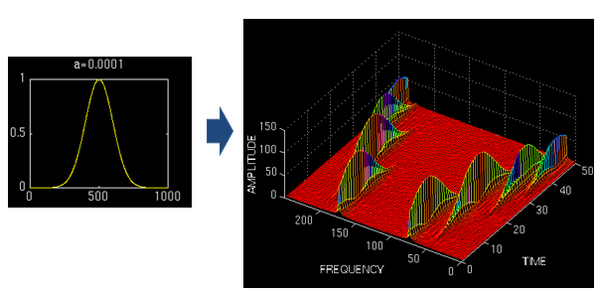
這個基函式會伸縮、會平移(其實本質並非平移,而是兩個正交基的分解)。縮得窄,對應高頻;伸得寬,對應低頻。然後這個基函式不斷和訊號做相乘。某一個尺度(寬窄)下乘出來的結果,就可以理解成訊號所包含的當前尺度對應頻率成分有多少。於是,基函式會在某些尺度下,與訊號相乘得到一個很大的值,因為此時二者有一種重合關係。那麼我們就知道訊號包含該頻率的成分的多少。
仔細體會可以發現,這一步其實是在計算訊號和三角函式的相關性。
<img src="https://pic2.zhimg.com/8fbc3a5f07a5ab0f0a90b65bc621ae21_b.jpg" data-rawwidth="452" data-rawheight="311" class="origin_image zh-lightbox-thumb" width="452" data-original="https://pic2.zhimg.com/8fbc3a5f07a5ab0f0a90b65bc621ae21_r.jpg">
 <img
src="https://pic3.zhimg.com/95cfa4aa2b2ea493cf07dbd4384d2526_b.jpg" data-rawwidth="509" data-rawheight="297" class="origin_image zh-lightbox-thumb" width="509" data-original="https://pic3.zhimg.com/95cfa4aa2b2ea493cf07dbd4384d2526_r.jpg">看,這兩種尺度能乘出一個大的值(相關度高),所以訊號包含較多的這兩個頻率成分,在頻譜上這兩個頻率會出現兩個峰。
<img
src="https://pic3.zhimg.com/95cfa4aa2b2ea493cf07dbd4384d2526_b.jpg" data-rawwidth="509" data-rawheight="297" class="origin_image zh-lightbox-thumb" width="509" data-original="https://pic3.zhimg.com/95cfa4aa2b2ea493cf07dbd4384d2526_r.jpg">看,這兩種尺度能乘出一個大的值(相關度高),所以訊號包含較多的這兩個頻率成分,在頻譜上這兩個頻率會出現兩個峰。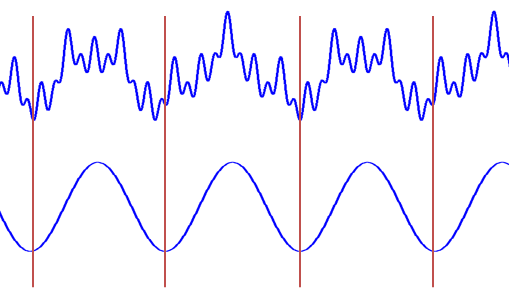 看,這兩種尺度能乘出一個大的值(相關度高),所以訊號包含較多的這兩個頻率成分,在頻譜上這兩個頻率會出現兩個峰。
看,這兩種尺度能乘出一個大的值(相關度高),所以訊號包含較多的這兩個頻率成分,在頻譜上這兩個頻率會出現兩個峰。以上,就是粗淺意義上傅立葉變換的原理。
如前邊所說,小波做的改變就在於,將無限長的三角函式基換成了有限長的會衰減的小波基。
<img src="https://pic3.zhimg.com/94b5f53d29d655e0a4d90fa867027eda_b.jpg" data-rawwidth="675" data-rawheight="477" class="origin_image zh-lightbox-thumb" width="675" data-original="https://pic3.zhimg.com/94b5f53d29d655e0a4d90fa867027eda_r.jpg">這就是為什麼它叫“小波”,因為是很小的一個波嘛~
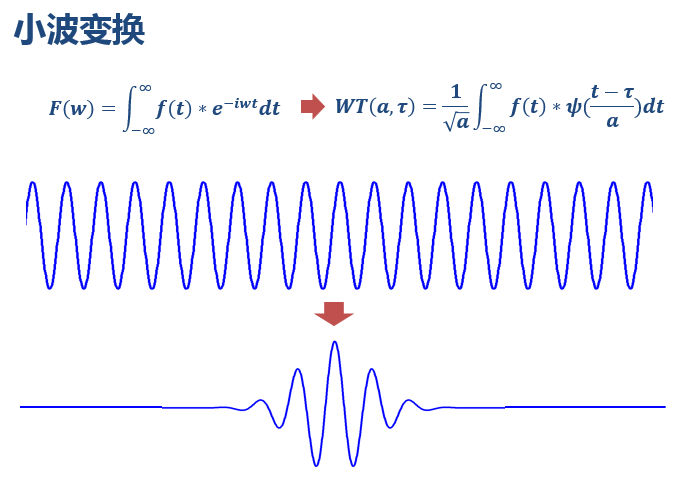 這就是為什麼它叫“小波”,因為是很小的一個波嘛~
這就是為什麼它叫“小波”,因為是很小的一個波嘛~<img src="https://pic1.zhimg.com/f3342ad8f9f814beecf82b29b0576ef0_b.jpg" data-rawwidth="389" data-rawheight="71" class="content_image" width="389">
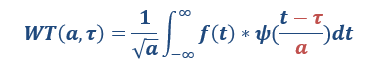
從公式可以看出,不同於傅立葉變換,變數只有頻率ω,小波變換有兩個變數:尺度a(scale)和平移量 τ(translation)。尺度a控制小波函式的伸縮,平移量 τ控制小波函式的平移。尺度就對應於頻率(反比),平移量 τ就對應於時間。
<img src="https://pic2.zhimg.com/c4aa4c1cc6fdc1feb47be1001fa67301_b.jpg" data-rawwidth="592" data-rawheight="341" class="origin_image zh-lightbox-thumb" width="592" data-original="https://pic2.zhimg.com/c4aa4c1cc6fdc1feb47be1001fa67301_r.jpg">
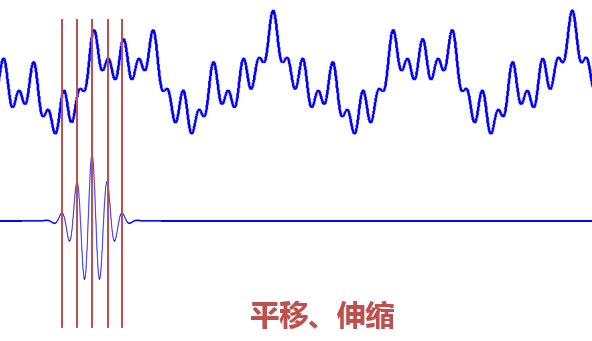
當伸縮、平移到這麼一種重合情況時,也會相乘得到一個大的值。這時候和傅立葉變換不同的是,這不僅可以知道訊號有這樣頻率的成分,而且知道它在時域上存在的具體位置。
而當我們在每個尺度下都平移著和訊號乘過一遍後,我們就知道訊號在每個位置都包含哪些頻率成分。
看到了嗎?有了小波,我們從此再也不害怕非穩定訊號啦!從此可以做時頻分析啦!
做傅立葉變換隻能得到一個頻譜,做小波變換卻可以得到一個時頻譜!
<img src="https://pic2.zhimg.com/27adabe9c43e9716543ac6e08a983505_b.jpg" data-rawwidth="277" data-rawheight="208" class="content_image" width="277"> ↑:時域訊號
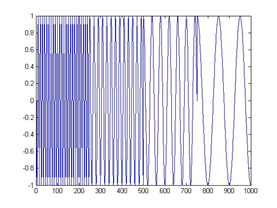 ↑:時域訊號
↑:時域訊號<img src="https://pic1.zhimg.com/f0511af35a25dcbfc760959bec38b6cc_b.jpg" data-rawwidth="404" data-rawheight="302" class="content_image" width="404">↑:傅立葉變換結果
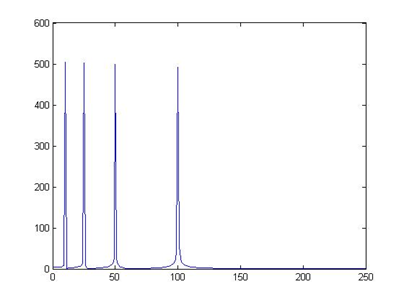 ↑:傅立葉變換結果
↑:傅立葉變換結果<img src="https://pic1.zhimg.com/cfae89c24cc167c028f02368ee509a68_b.jpg" data-rawwidth="524" data-rawheight="403" class="origin_image zh-lightbox-thumb" width="524" data-original="https://pic1.zhimg.com/cfae89c24cc167c028f02368ee509a68_r.jpg"> ——此影象來源於“THE WAVELET TUTORIAL”
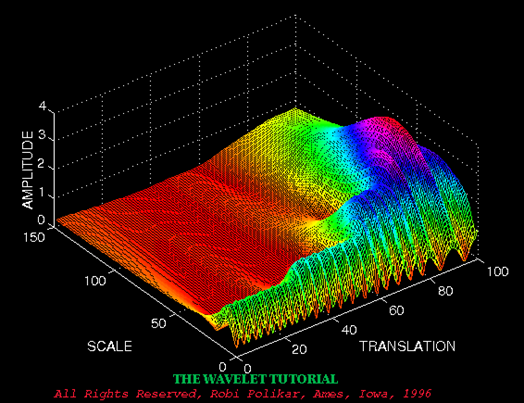 ——此影象來源於“THE WAVELET TUTORIAL”
——此影象來源於“THE WAVELET TUTORIAL”↑:小波變換結果
小波還有一些好處,比如,我們知道對於突變訊號,傅立葉變換存在吉布斯效應,我們用無限長的三角函式怎麼也擬合不好突變訊號:
<img src="https://pic3.zhimg.com/c6041e8710f31ab327e215467d2c58d2_b.jpg" data-rawwidth="691" data-rawheight="474" class="origin_image zh-lightbox-thumb" width="691" data-original="https://pic3.zhimg.com/c6041e8710f31ab327e215467d2c58d2_r.jpg">然而衰減的小波就不一樣了:
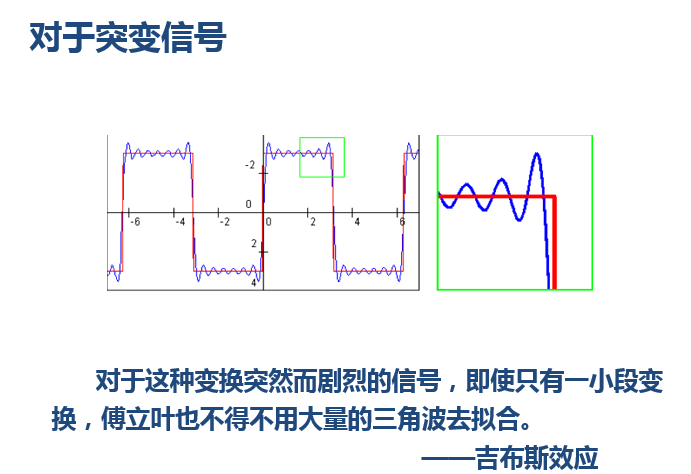 然而衰減的小波就不一樣了:
然而衰減的小波就不一樣了:<img src="https://pic3.zhimg.com/d03e5344001f6fb2dc10be4a7bd2af92_b.jpg" data-rawwidth="677" data-rawheight="522" class="origin_image zh-lightbox-thumb" width="677" data-original="https://pic3.zhimg.com/d03e5344001f6fb2dc10be4a7bd2af92_r.jpg">
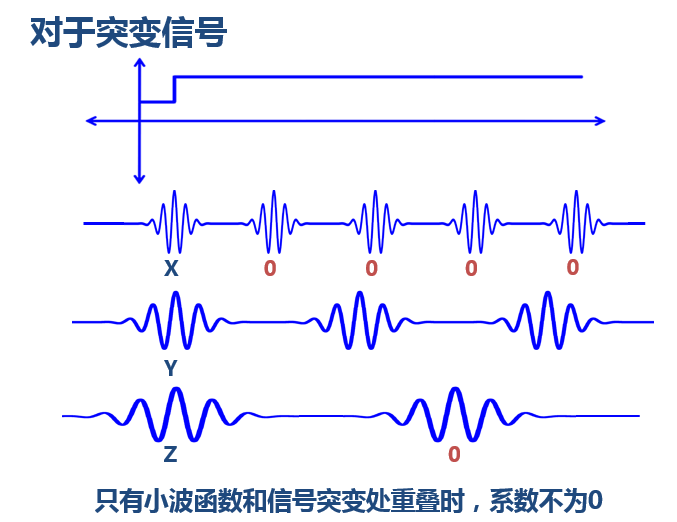
以上,就是小波的意義。
相關推薦
傅立葉變化,短時傅立葉分析,小波變換
從傅立葉變換到小波變換,並不是一個完全抽象的東西,可以講得很形象。小波變換有著明確的物理意義,如果我們從它的提出時所面對的問題看起,可以整理出非常清晰的思路。 下面我就按照傅立葉-->短時傅立葉變換-->小波變換的順序,講一下為什麼會出現小波這個東西、小波究竟是怎樣的思路。(反正題主要求的是通俗形
頻域處理:傅立葉變換及小波變換
頻域處理:傅立葉變換及小波變換 引言 1、傅立葉變換 2、小波變換 3、程式 引言 影象處理–>頻域處理–>傅立葉變換、小波變換。用另一種方法來觀察世界的話,你會發現世界是永恆不變的。
訊號處理、傅立葉變換 、小波變換的入門資料
以下摘錄來自“王昱博,訊號處理博士僧”的回答 在傅立葉變換中,如果一個訊號在實數域滿足勒貝格可度量條件(Lebesgue-measurable)則這個訊號的傅立葉變換收斂。通過傅立葉變換我們可以看到的是訊號的時域特徵被完全的變換到了頻率域。這時在時域中不明顯的週期性變化被直觀的反應到了對應的頻率域。數學上
【轉載】小波變換與傅立葉變換
一、基的概念 小波函式和正餘弦函式都是基,訊號都可以分成無窮多個他們的和。而展開係數就是基與訊號之間的內積,更通俗的說是投影。展開係數大的,說明訊號和基是足夠相似的,這就是相似性檢測的思想。但我們必須明確的是,傅立葉是0-2π標準正交基,而小波是-inf到inf
從傅立葉變換到小波變換的分析 學習筆記
感謝前輩的分析和總結 小波,一個神奇的波,可長可短可胖可瘦(伸縮平移),當去學習小波的時候,第一個首先要做的就是回顧傅立葉變換(又回來了,唉),因為他們都是頻率變換的方法,而傅立葉變換是最入門的,也是最先了解的,通過傅立葉變換,瞭解缺點,改進,慢慢的就
數學不好、英語不好、非本專業,想學Python資料分析,有救嗎?
“非本專業想轉型做資料分析,有救嗎?” “數學不好,英語不好,想學Python資料分析,有救嗎?” “不懂Python資料分析到底是什麼,有救嗎?” 我的答案是 妥妥有救! 大家好,我是大鵬,目前在城市資料團,是一名資料分析師。 準確來說,我是一名非本專業的轉行資料分析師,
一維小波變換,可多次分解
4、測試結果: 輸入訊號x(i)為: 取f1 = 5, f2 = 10, f0 = 320, n = 512。x(i)如圖1所示: 圖1 輸入訊號 各級分解的結果如圖2~圖7所示,左半部分為尺度係數,右半部分為小波係數: 圖21級分解結果 圖32級分解結果 圖43級分解結果 圖54級分解結
數字影象處理,基於小波變換的影象對比度增強演算法
小波變換下的影象對比度增強技術實質上是通過小波變換把影象訊號分解成不同子帶,針對不同子帶應用不同的演算法來增強不同頻率範圍內的影象分量,突出不同尺度下的近似和細節,從而達到增強影象層次感的
關於嵌入式和java,網際網路的行業統計分析,判斷未來房地產以及發展趨勢
上圖是java崗位的,分別是成都,武漢,杭州,廣州,可以看出武漢和廣州在java工程師上的崗位招聘數量基本持平,可是廣州的房價卻是最高的 ==================================================分界限========
matlab 時頻分析 短時傅立葉變換 STFT
分享一下我老師大神的人工智慧教程!零基礎,通俗易懂!http://blog.csdn.net/jiangjunshow 也歡迎大家轉載本篇文章。分享知識,造福人民,實現我們中華民族偉大復興!
Python scipy 計算短時傅立葉變換(Short-time Fourier transforms)
計算短時傅立葉變換(STFT) scipy.signal.stft(x,fs = 1.0,window ='hann',nperseg = 256,noverlap = None,nfft = None,detrend = False,return_onesided = True,boundary ='ze
短時傅立葉變換
【音訊處理】短時傅立葉變換 https://blog.csdn.net/zb1165048017/article/details/80682473 2) c++加窗 https://blog.csdn.net/jacke121/article/details/61917610
傅立葉變化(轉)
記得上大學的時候的機械振動還有工程測試利用的傅立葉變化,當時感覺雲裡霧裡的,感覺好難,也就沒有去搞,渾水摸魚也就過來了,然後現在到了研究生階段,發現傅立葉變換呀,卷積呀非常的重要,也是學術研究最基礎的工具。在做人臉識別的時候剛好用上,所以靜下心來學習一下,找了一些資料,感覺不
11.頻域裡的卷積——介紹,傅立葉變換和卷積,快速傅立葉變換(FFT)_1
目錄 介紹 FFT 介紹 我們將繼續討論頻率分析以及如何用頻率分量的概念來研究影象。如果你還記得上次我們講過的基於頻率的影象分解的概念。我們通過給你們看這張照片來回憶它(如圖)。這是著名的Dali圖片,當你在那裡允許高頻影象時,你會看到一個女人在欣賞地中海之類的東
【機器學習筆記32】短時傅立葉變換
傅立葉變換的侷限性 1 需要利用訊號的全部時域資訊; 2 沒有反應頻率隨時間變換的訊號情況; 短時傅立葉變換 1964年Gabor提出了短時傅立葉變換(有叫Gabor變換),即在傳統的傅立葉變換的基礎上加了一個時間窗。如下: Sw(x,t)=∫x(τ)m(τ−
負數,傅立葉變換,反傅立葉變換(錯)
#include <QCoreApplication> #include "C:\Users\Administrator\Desktop\fftw\fftw-3.3.4-dll32\fftw3.h" #include "D:\Qt\Eigen\Dense" #include <stdi
c語言之傅立葉變化
#include <stdio.h> void StartTimer0(void); void Interrupt_Init(void); void Interrupt_Start(void); #if 0 void main (void) { printf
基於二維傅立葉變化法的MRI成像原理的Matlab模擬(2)
二、MRI模擬資料的獲取 基於(1)中的分析,我們知道K空間和影象空間是一對傅立葉變換的關係。因此,模擬資料獲取可以通過對原始影象做2-D FT來實現。而為了驗證模擬資料獲取的正確性,可以對模擬資料做2-D IFT,得到重建後的影象,比較原始影象和重建影象,
spectrogram函式做短時傅立葉分析
整理自:http://blog.sina.com.cn/s/blog_6163bdeb0102dwfw.html 今天偶人發現原來matlab自帶了短時傅立葉變換的分析函式,老版本的matlab是specgram函式,新的改成了spectrogram函式,雖然一說到時頻分析,都會說到小波分析,小波分析要比短
短時傅立葉變換的原理與應用:電話撥號聲分析(4)
現在要做的就是,對於每一幀(語譜圖中,固定時間k,頻率從0 - f_sample/2),把應該可以分別歸到697、770、……、1633 Hz這些類的頻率組分所對應的DFT的模值,都加起來。意思是,把從 0 - F_sample/2的頻率,換算成第#1 - #8,一共8個頻率組別。語言的表達是不客觀,不清晰。
