spectrogram函式做短時傅立葉分析
整理自:http://blog.sina.com.cn/s/blog_6163bdeb0102dwfw.html
今天偶人發現原來matlab自帶了短時傅立葉變換的分析函式,老版本的matlab是specgram函式,新的改成了spectrogram函式,雖然一說到時頻分析,都會說到小波分析,小波分析要比短時傅立葉要好云云,但在分析訊號的瞬時頻譜時,短時傅立葉還是有它的用武之地的。前一陣也看了一些有關小波分析的matlab實現,發現幫助中使用小波也多是除噪、壓縮,都說小波是時頻顯微鏡,它的用武之地還是在於檢視高頻在哪一級分解中,進而可以有效濾除一些訊號,比如除噪,所以短時傅立葉變換檢視瞬時頻率正好互補一下。時頻分析還認識的不深,一個階段的想法而已。
另外,之前對matlab的掃頻函式chirp做過總結,見http://blog.sina.com.cn/s/blog_6163bdeb0100qbqo.html,裡面就是使用spectrogram函式來檢視產生的掃頻訊號的瞬時頻率的,當時不知道那個函式是幹啥,就感覺好神奇,現在正好看到,總結一下吧!
spectrogram
功能:使用短時傅立葉變換得到訊號的頻譜圖。
語法:
[S,F,T,P]=spectrogram(x,window,noverlap,nfft,fs)
[S,F,T,P]=spectrogram(x,window,noverlap,F,fs)
說明: 當使用時無輸出引數,會自動繪製頻譜圖;有輸出引數,則會返回輸入訊號的短時傅立葉變
換。當然也可以從函式的返回值S,F,T,P繪製頻譜圖,具體參見例子。
引數:
x---輸入訊號的向量。預設情況下,即沒有後續輸入引數,x將被分成8段分別做變換處理,
如果x不能被平分成8段,則會做截斷處理。預設情況下,其他引數的預設值為
window---窗函式,預設為nfft長度的海明窗Hamming
noverlap---每一段的重疊樣本數,預設值是在各段之間產生50%的重疊
nfft---做FFT變換的長度,預設為256和大於每段長度的最小2次冪之間的最大值。
另外,此引數除了使用一個常量外,還可以指定一個頻率向量F
fs---取樣頻率,預設值歸一化頻率
Window---窗函式,如果window為一個整數,x將被分成window段,每段使用Hamming窗函式加窗。
如果window是一個向量,x將被分成length(window)段,每一段使用window向量指定的
窗函式加窗。所以如果想獲取specgram函式的功能,只需指定一個256長度的Hann窗。
Noverlap---各段之間重疊的取樣點數。它必須為一個小於window或length(window)的整數。
其意思為兩個相鄰窗不是尾接著頭的,而是兩個窗有交集,有重疊的部分。
Nfft---計算離散傅立葉變換的點數。它需要為標量。
Fs---取樣頻率Hz,如果指定為[],預設為1Hz。
S---輸入訊號x的短時傅立葉變換。它的每一列包含一個短期區域性時間的頻率成分估計,
時間沿列增加,頻率沿行增加。
如果x是長度為Nx的覆信號,則S為nfft行k列的復矩陣,其中k取決於window,
如果window為一個標量,則k = fix((Nx-noverlap)/(window-noverlap))
如果window為向量,則k = fix((Nx-noverlap)/(length(window)-noverlap))
對於實訊號x,如果nfft為偶數,則S的行數為(nfft/2+1),如果nfft為奇數,
則行數為(nfft+1)/2,列數同上。
F---在輸入變數中使用F頻率向量,函式會使用Goertzel方法計算在F指定的頻率處計算頻譜圖。
指定的頻率被四捨五入到與訊號解析度相關的最近的DFT容器(bin)中。而在其他的使用nfft
語法中,短時傅立葉變換方法將被使用。對於返回值中的F向量,為四捨五入的頻率,其長度
等於S的行數。
T---頻譜圖計算的時刻點,其長度等於上面定義的k,值為所分各段的中點。
P---能量譜密度PSD(Power Spectral Density),
對於實訊號,P是各段PSD的單邊週期估計;
對於覆信號,當指定F頻率向量時,P為雙邊PSD。
P矩陣的元素計算公式如下P(I,j)=k|S(I,j)|2,其中的的k是實值標量,定義如下
對於單邊PSD,計算公式如下,其中w(n)表示窗函式,Fs為取樣頻率,在0頻率和奈奎斯特
頻率處,分子上的因子2改為1;
對於雙邊PSD,計算公式如下
如果取樣頻率沒有指定,分母上的Fs由2*pi代替。
spectrogram(...)當呼叫函式時沒有輸出引數,將會自動繪製各段的PSD估計,繪製的命令如下
surf(T,F,10*log10(abs(P)));
axis tight;
view(0,90);
spectrogram(...,'freqloc')使用freqloc字串可以控制頻率軸顯示的位置。當freqloc=xaxis
時,頻率軸顯示在x軸上,當freqloc=yaxis時,頻率軸顯示在y軸上,預設是顯示在x軸
上。如果在指定freqloc的同時,又有輸出變數,則freqloc將被忽略。
例.計算並顯示二次掃頻訊號的PSD圖,掃頻訊號的頻率開始於100Hz,在1s時經過200Hz
T = 0:0.001:2;
X = chirp(T,100,1,200,'q');
spectrogram(X,128,120,128,1E3);
title('Quadratic Chirp');
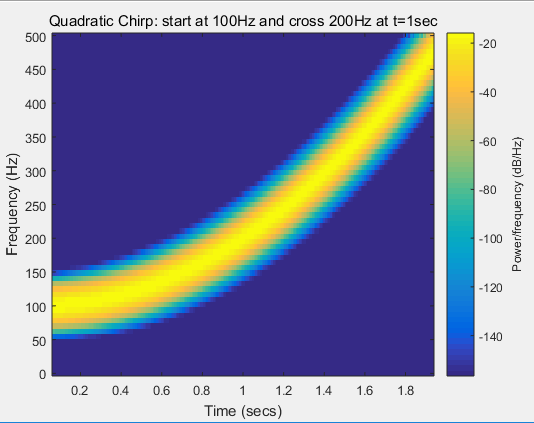
頻率顯示在y軸上:
t=0:0.001:2; % 2 secs @ 1kHz sample rate
y=chirp(t,100,1,200,'q'); % Start @ 100Hz, cross 200Hz at t=1sec
spectrogram(y,kaiser(128,18),120,128,1E3,'yaxis');
title('Quadratic Chirp: start at 100Hz and cross 200Hz at t=1sec');
例.計算並顯示線性掃頻訊號的PSD圖,掃頻訊號由直流開始,在1s時經過150Hz,控制頻率軸顯示在y軸上
T = 0:0.001:2;
X = chirp(T,0,1,150);
[S,F,T,P] = spectrogram(X,256,250,256,1E3);
surf(T,F,10*log10(P),'edgecolor','none'); axis tight;
view(0,90);
xlabel('Time (Seconds)'); ylabel('Hz');
函式使用的注意:
nfft越大,頻域的解析度就越高(解析度=fs/nfft),但離瞬時頻率就越遠;
noverlap影響時間軸的解析度,越接近nfft,解析度越高,相應的冗餘就越多,計算量越大,但計算機只要能承受,問題不大。