直線繪製光柵化演算法

1.數值微分DDA（Digital Differential Analyzer）演算法

1.1原理

引入增量思想，以dx≥dy（斜率[0,1]）為例，考慮直線y=kx+b，當x步進為1時，y步進為k，即yi+1=yi+k，根據四捨五入法即可繪製直線

1.2虛擬碼

y = y1;
for(x:[x1,x2])
{
    drawPixel(x,y);
    y += k;
}

1.3實現程式碼

/************************************************************************/
 

/* 數值微分DDA(Digital Differential Analyzer)演算法                        */
/************************************************************************/
void drawline(int x1,int y1,int x2,int y2,acolor color)
{
    int dx = abs(x2 - x1);
    int dy = abs(y2 - y1);
    if (dx>=dy) //以dx=1為步進，否則會出現斷點
    {
        if
 
 (x1>x2)
        {
            swap(x1,x2);
            swap(y1,y2);
        }
        float k = static_cast<float>(y2-y1)/(x2-x1);
        float y = y1;
        for (int x=x1;x<=x2;++x)
        {
            drawpixel(x,y,color);
            y += k;
        }
    }
    else
    {
        if
 
 (y1>y2)
        {
            swap(x1,x2);
            swap(y1,y2);
        }
        float k = static_cast<float>(x2-x1)/(y2-y1);
        float x = x1;
        for (int y=y1;y<=y2;++y)
        {
            drawpixel(x,y,color);
            x += k;
        }
    }   
}

DDA演算法原理簡單明瞭，但是由於存在浮點數的加減運算，所以效率還需提高。

2.中點畫線演算法

2.1原理

通過一般式Ax+By+C=0來繪製直線，同樣考慮斜率[0,1]情況,對於任意一點P(x，y)我們可以通過B（Ax+By+C）的正負來判斷點P相對於直線的位置，>0時點在直線的上方，=0則在直線上，<0則在直線下方。根據這個原理，我們可以通過判斷點（xi+1,yi+0.5）相對於直線的位置來進行直線取點。
我們把中點代入f(x,y)
　　d0=f(xi+1,yi+0.5)=Axi+Byi+C+A+0.5B=A+0.5B
若取上點，則
　　d1=f(xi+2,yi+1.5)=d0+A+B
若取下點，則
　　d1=f(xi+2,yi+0.5)=d0+A
這裡我們可以將d乘以2以消除浮點數，避免浮點數運算的開銷，提高運算效率

2.2虛擬碼

d = 2A+B;
y = y1;
for(x:[x1,x2])
{
    drawPixel(x,y);
    if(d<0) //中點在直線下方，取上點
    {
        d += 2(A+B);
        ++y;
    }
    else
    {
        d += 2A;
    }
}

2.3實現程式碼

/************************************************************************/
/* 繪製直線(中點法)
 * 隱式方程f(x,y)=(y1-y1)x+(x2-x1)y+x1y2-x2y1=0
 * B*f(x,y)>0為上,<0為下,每次用中點（x+1,y±0.5）帶入進行比較
 * 此處取B>0,即可直接判斷
 */                                                                     
/************************************************************************/
void drawLine(int x1,int y1,int x2,int y2,AColor color)
{
    int dx = abs(x2 - x1);
    int dy = abs(y2 - y1);
    if (dx>=dy)                                     //以dx=1為步進，否則會出現斷點
    {
        if (x1>x2)
        {
            swap(x1,x2);
            swap(y1,y2);
        }
        int A = y1-y2;
        int B = x2-x1;
        if(y2>=y1)                                  //斜率[0,1]
        {
            int d = (A<<1) + B;                     //f(x+1,y+0.5)*2以消除浮點數運算
            int upIncrement = (A+B)<<1;             //取上點時d的增量
            int downTncrement = A<<1;               //取下點時d的增量
            for (int x=x1,y=y1;x<=x2;++x)
            {
                drawPixel(x,y,color);
                if (d<0){                           //中點在直線下，取上點
                    d += upIncrement;
                    ++y;
                }
                else
                {
                    d += downTncrement;
                }
            }
        }
        else                                        //斜率[-1,0)
        {
            int d = (A<<1) - B;                 
            int upIncrement = A<<1;         
            int downTncrement = (A-B)<<1;                   
            for (int x=x1,y=y1;x<=x2;++x)
            {
                drawPixel(x,y,color);
                if (d<0){                               
                    d += upIncrement;
                }
                else
                {
                    d += downTncrement;
                    --y;
                }
            }
        }   
    }
    else
    {
        if (y1>y2)
        {
            swap(x1,x2);
            swap(y1,y2);
        }
        int A = x1-x2;
        int B = y2-y1;
        if (x2>=x1)
        {
            int d = (A<<1) + B;                 //f(x+0.5,y+1)*2以消除浮點數運算,此處Ay+Bx+C=0
            int upIncrement = (A+B)<<1;         //取上點時d的增量
            int downTncrement = A<<1;           //取下點時d的增量
            for (int x=x1,y=y1;y<=y2;++y)
            {
                drawPixel(x,y,color);
                if (d<0){                       //中點在直線下，取上點
                    d += upIncrement;
                    ++x;
                }
                else
                {
                    d += downTncrement;
                }
            }
        }
        else
        {
            int d = (A<<1) - B;                 
            int upIncrement = A<<1;         
            int downTncrement = (A-B)<<1;           
            for (int x=x1,y=y1;y<=y2;++y)
            {
                drawPixel(x,y,color);
                if (d<0){                       
                    d += upIncrement;
                }
                else
                {
                    d += downTncrement;
                    --x;
                }
            }
        }
    }   
}

3.Bresenham演算法

3.1原理

同樣從簡單的開始考慮（斜率[0,1]），當x步進1時，y提高k，則我們用d記錄提高量，一旦d>0.5，我們便取上點，並對d進行減1操作。同樣，這樣也會出現浮點數加減法運算，首先我們可以通過e=d-0.5的正負來進行判斷，因為對d-0.5的正乘法不會影響其符號，所以我們可以進行如下改變：
第一步：(d-0.5)*2 = 2d-1，消除0.5這個浮點數。
由於d=dy/dx（dy=y2-y1,dx=x2-x1）同樣會產生浮點數，因為斜率為[0,1]，所以我們可以保證dx>0
第二步：(2d-1)*dx = 2dy-dx，此時浮點數完全被消除。

3.2虛擬碼

k = 2dy;
e = -dx;
for(x:[x1,x2])
{
    drawPixel(x,y);
    e += k;
    if(e>0)
    {
        ++y;
        e -= 2dx;
    }
}

3.3實現程式碼

/************************************************************************/
/* Bresenham演算法   
 * 主要通過e=d±0.5判斷符號
*/
/************************************************************************/
void drawLine(int x1,int y1,int x2,int y2,AColor color)
{
    int dx = abs(x2 - x1);
    int dy = abs(y2 - y1);
    if (dx>=dy)                                     //以dx=1為步進，否則會出現斷點
    {
        if (x1>x2)
        {
            swap(x1,x2);
            swap(y1,y2);
        }
        int flag = y2>=y1?1:-1;                     //斜率[-1,1]
        int k = flag*(dy<<1);
        int e = -dx*flag;
        for (int x=x1,y=y1;x<=x2;++x) 
        {
            drawPixel(x,y,color);
            e += k;
            if (flag*e>0)
            {
                y += flag;
                e -= 2*dx*flag;
            }
        }
    }
    else
    {
        if (y1>y2)
        {
            swap(x1,x2);
            swap(y1,y2);
        }
        int flag = x2>x1?1:-1;
        int k = flag*(dx<<1);
        int e = -dy*flag;
        for (int x=x1,y=y1;y<=y2;++y) 
        {
            drawPixel(x,y,color);
            e += k;
            if (flag*e>0)
            {
                x += flag;
                e -= 2*dy*flag;
            }
        }
    }
}

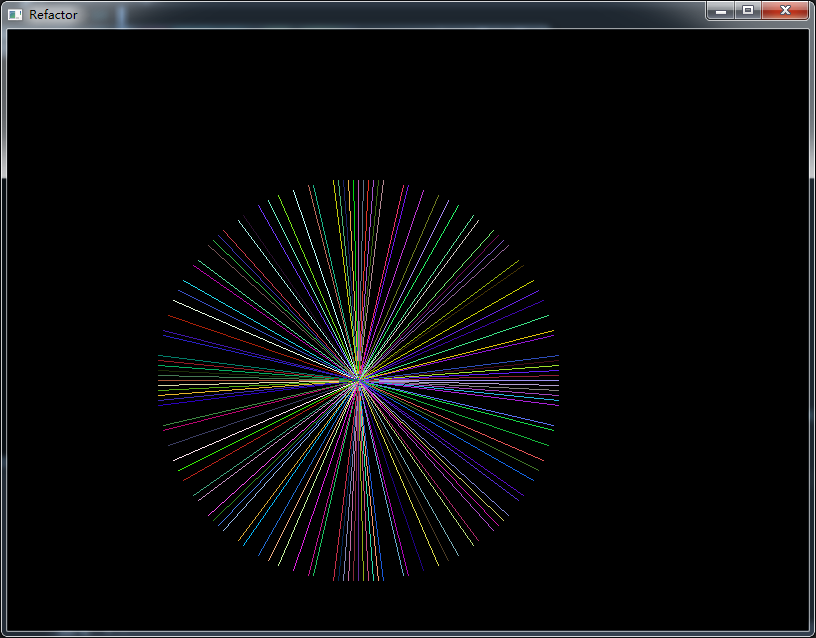
4.效果圖

繪製一個圓中的一些半徑，圓心（350,350）

for (int i=0;i<580;i+=5)
    {
        for (int j=0;j<580;j+=5)
        {
            double v = sqrt(pow(i-350,2)+pow(j-350,2))-200;
            if ( v>=0&&v < 2)
            {      
                drawline(350,350,i,j,AColor(0,(1+rand()%255)/255.0f,(1+rand()%255)/255.0f,(1+rand()%255)/255.0f));            
            }
        }
    }

專案完整地址：