克魯斯卡爾演算法：

【1】克魯斯卡爾演算法

普里姆演算法是以某頂點為起點，逐步找各頂點上最小權值的邊來構建最小生成樹。

克魯斯卡爾演算法是直接以邊為目標去構建。

因為權值是在邊上，直接去找最小權值的邊來構建生成樹也是很自然的想法，只不過構建時要考慮是否會形成環路而已。

此時我們用到了圖的儲存結構中的邊集陣列結構。

以下是邊集陣列結構的定義程式碼：

本演算法所用同普里姆演算法的例項，我們直接建立圖的邊集陣列。

並對邊的權值從小到大排序後如下圖：

【2】克魯斯卡爾演算法及詳解

克魯斯卡爾演算法及其詳解：

鑑於此演算法很簡單，當 i=0, i=1, i=2時執行結果可以眼觀，不再贅述。直接分析重點：

此演算法的Find函式由邊數e決定，時間複雜度為O(loge),而外面有一個for迴圈e次。

所以克魯斯卡爾演算法的時間複雜度為O(eloge)

對比兩個演算法：

克魯斯卡爾演算法主要針對邊展開，邊數少時效率會很高，所以對於稀疏圖有優勢

而普利姆演算法對於稠密圖，即邊數非常多的情況會好些。

【3】克魯斯卡爾演算法實現

實現程式碼如下：

/克魯斯卡爾演算法
//在連通網中求出最小生成樹

#include <stdio.h>
#include <stdlib.h>

#define MAXEDGE 20
#define MAXVEX  20
#define INFINITY 65535

typedef struct
{
    int arc[MAXVEX][MAXVEX];
    int numVertexes, numEdges;//頂點數，邊數
}MGraph;

typedef struct
{
    int begin;
    int end;
    int weight;
}Edge;   //對邊集陣列Edge結構的定義

//建立圖的鄰接矩陣
void CreateMGraph(MGraph *G) {
    int i, j;

    G->numEdges=11;
    G->numVertexes=7;

    for (i = 0; i < G->numVertexes; i++) {
        for ( j = 0; j < G->numVertexes; j++) {
            if (i==j)
                G->arc[i][j]=0;
            else
                G->arc[i][j] = G->arc[j][i] = INFINITY;
        }
    }
    G->arc[0][1]=7;
    G->arc[0][3]=5;
    G->arc[1][2]=8;
    G->arc[1][3]=9;
    G->arc[1][4]=7;
    G->arc[2][4]=5;
    G->arc[3][4]=15;
    G->arc[3][5]=6;
    G->arc[4][5]=8;
    G->arc[4][6]=9;
    G->arc[5][6]=11;

    for(i = 0; i < G->numVertexes; i++) {
        for(j = i; j < G->numVertexes; j++) {
            G->arc[j][i] =G->arc[i][j];
        }
    }

}

//快速排序的條件
int cmp(const void* a, const void* b) {
    return (*(Edge*)a).weight - (*(Edge*)b).weight;
}

//找到根節點
int Find(int *parent, int f) {
    while ( parent[f] > 0) {
        f = parent[f];
    }
    return f;
}

// 生成最小生成樹
void MiniSpanTree_Kruskal(MGraph G) {
    int i, j, n, m;
    int k = 0;
    int parent[MAXVEX]; //用於尋找根節點的陣列

    Edge edges[MAXEDGE]; //定義邊集陣列,edge的結構為begin,end,weight,均為整型

    // 用來構建邊集陣列並排序(將鄰接矩陣的對角線右邊的部分存入邊集陣列中)
    for ( i = 0; i < G.numVertexes-1; i++) {
        for (j = i + 1; j < G.numVertexes; j++) {
            if (G.arc[i][j] < INFINITY) {
                edges[k].begin = i; //編號較小的結點為首
                edges[k].end = j;   //編號較大的結點為尾
                edges[k].weight = G.arc[i][j];
                k++;
            }
        }
    }

    //為邊集陣列Edge排序
    qsort(edges, G.numEdges, sizeof(Edge), cmp);

    for (i = 0; i < G.numVertexes; i++)
        parent[i] = 0;

    printf("列印最小生成樹：\n");
    for (i = 0; i < G.numEdges; i++) {
        n = Find(parent, edges[i].begin);//尋找邊edge[i]的“首節點”所在樹的樹根
        m = Find(parent, edges[i].end);//尋找邊edge[i]的“尾節點”所在樹的樹根

        //假如n與m不等，說明兩個頂點不在一棵樹內，因此這條邊的加入不會使已經選擇的邊集產生迴路
        if (n != m) {
            parent[n] = m;
            printf("(%d, %d) %d\n", edges[i].begin, edges[i].end, edges[i].weight);
        }
    }
}

int main(void)
{
    MGraph G;
    CreateMGraph(&G);
    MiniSpanTree_Kruskal(G);

    return 0;
}
 

普里姆(Prim)演算法，和克魯斯卡爾演算法一樣，是用來求加權連通圖的最小生成樹的演算法。

基本思想 
對於圖G而言，V是所有頂點的集合；現在，設定兩個新的集合U和T，其中U用於存放G的最小生成樹中的頂點，T存放G的最小生成樹中的邊。 從所有uЄU，vЄ(V-U) (V-U表示出去U的所有頂點)的邊中選取權值最小的邊(u, v)，將頂點v加入集合U中，將邊(u, v)加入集合T中，如此不斷重複，直到U=V為止，最小生成樹構造完畢，這時集合T中包含了最小生成樹中的所有邊。

普里姆演算法圖解

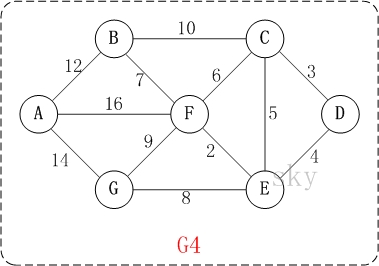
以上圖G4為例，來對普里姆進行演示(從第一個頂點A開始通過普里姆演算法生成最小生成樹)。

初始狀態：V是所有頂點的集合，即V={A,B,C,D,E,F,G}；U和T都是空！ 
第1步：將頂點A加入到U中。 
    此時，U={A}。 
第2步：將頂點B加入到U中。 
    上一步操作之後，U={A}, V-U={B,C,D,E,F,G}；因此，邊(A,B)的權值最小。將頂點B新增到U中；此時，U={A,B}。 
第3步：將頂點F加入到U中。 
    上一步操作之後，U={A,B}, V-U={C,D,E,F,G}；因此，邊(B,F)的權值最小。將頂點F新增到U中；此時，U={A,B,F}。 
第4步：將頂點E加入到U中。 
    上一步操作之後，U={A,B,F}, V-U={C,D,E,G}；因此，邊(F,E)的權值最小。將頂點E新增到U中；此時，U={A,B,F,E}。 
第5步：將頂點D加入到U中。 
    上一步操作之後，U={A,B,F,E}, V-U={C,D,G}；因此，邊(E,D)的權值最小。將頂點D新增到U中；此時，U={A,B,F,E,D}。 
第6步：將頂點C加入到U中。 
    上一步操作之後，U={A,B,F,E,D}, V-U={C,G}；因此，邊(D,C)的權值最小。將頂點C新增到U中；此時，U={A,B,F,E,D,C}。 
第7步：將頂點G加入到U中。 
    上一步操作之後，U={A,B,F,E,D,C}, V-U={G}；因此，邊(F,G)的權值最小。將頂點G新增到U中；此時，U=V。

此時，最小生成樹構造完成！它包括的頂點依次是：A B F E D C G。

普里姆演算法的程式碼說明

以"鄰接矩陣"為例對普里姆演算法進行說明，對於"鄰接表"實現的圖在後面會給出相應的原始碼。

1. 基本定義

// 鄰接矩陣
typedef struct _graph
{
    char vexs[MAX];       // 頂點集合
    int vexnum;           // 頂點數
    int edgnum;           // 邊數
    int matrix[MAX][MAX]; // 鄰接矩陣
}Graph, *PGraph;

// 邊的結構體
typedef struct _EdgeData
{
    char start; // 邊的起點
    char end;   // 邊的終點
    int weight; // 邊的權重
}EData;

Graph是鄰接矩陣對應的結構體。 
vexs用於儲存頂點，vexnum是頂點數，edgnum是邊數；matrix則是用於儲存矩陣資訊的二維陣列。例如，matrix[i][j]=1，則表示"頂點i(即vexs[i])"和"頂點j(即vexs[j])"是鄰接點；matrix[i][j]=0，則表示它們不是鄰接點。 
EData是鄰接矩陣邊對應的結構體。

2. 普里姆演算法

#include<stdio.h>
#include<stdlib.h>
#include<malloc.h>
#include<string.h>
#define MAX 100
#define INF (~(0x1<<31))
typedef struct Graph
{
    char vexs[MAX];
    int vexnum;
    int edgnum;
    int matrix[MAX][MAX];
} Graph,*PGraph;

typedef struct EdgeData
{
    char start;
    char end;
    int weight;
} EData;

static int get_position(Graph g,char ch)
{
    int i;
    for(i=0; i<g.vexnum; i++)
        if(g.vexs[i]==ch)
            return i;
    return -1;
}

Graph* create_graph()
{
    char vexs[]= {'A','B','C','D','E','F','G'};
    int matrix[][7]=
    {
        {0,12,INF,INF,INF,16,14},
        {12,0,10,INF,INF,7,INF},
        {INF,10,0,3,5,6,INF},
        {INF,INF,3,0,4,INF,INF},
        {INF,INF,5,4,0,INF,8},
        {16,7,6,INF,2,0,9},
        {14,INF,INF,INF,8,9,0}
    };
    int vlen=sizeof(vexs)/sizeof(vexs[0]);
    int i,j;
    Graph *pG;
    if((pG=(Graph*)malloc(sizeof(Graph)))==NULL)
        return NULL;
    memset(pG,0,sizeof(pG));
    pG->vexnum=vlen;
    for(i=0; i<pG->vexnum; i++)
        pG->vexs[i]=vexs[i];
    for(i=0; i<pG->vexnum; i++)
        for(j=0; j<pG->vexnum; j++)
            pG->matrix[i][j]=matrix[i][j];
    for(i=0; i<pG->vexnum; i++)
    {
        for(j=0; j<pG->vexnum; j++)
        {
            if(i!=j&&pG->matrix[i][j]!=INF)
                pG->edgnum++;
        }
    }
    pG->edgnum/=2;
    return pG;
}

void print_graph(Graph G)
{
    int i,j;
    printf("Matrix Graph: \n");
    for(i=0; i<G.vexnum; i++)
    {
        for(j=0; j<G.vexnum; j++)
            printf("%10d ",G.matrix[i][j]);
        printf("\n");
    }
}

EData* get_edges(Graph G)
{
    EData *edges;
    edges=(EData*)malloc(G.edgnum*sizeof(EData));
    int i,j;
    int index=0;
    for(i=0; i<G.vexnum; i++)
    {
        for(j=i+1; j<G.vexnum; j++)
        {
            if(G.matrix[i][j]!=INF)
            {
                edges[index].start=G.vexs[i];
                edges[index].end=G.vexs[j];
                edges[index].weight=G.matrix[i][j];
                index++;
            }
        }
    }
    return edges;
}

void prim(Graph G,int start)
{
    int min,i,j,k,m,n,sum;
    int index=0;
    char prim[MAX];
    int weight[MAX];

    prim[index++]=G.vexs[start];

    for(i=0; i<G.vexnum; i++)
        weight[i]=G.matrix[start][i];
    weight[start]=0;

    for(i=0; i<G.vexnum; i++)
    {
       //i用來控制迴圈的次數，每次加入一個結點，但是因為start已經加入，所以當i為start是跳過
        if(start==i)
            continue;
        j=0;
        k=0;
        min=INF;
        for(k=0; k<G.vexnum; k++)
        {
            if(weight[k]&&weight[k]<min)
            {
                min=weight[k];
                j=k;
            }
        }
        sum+=min;
        prim[index++]=G.vexs[j];
        weight[j]=0;
        for(k=0; k<G.vexnum; k++)
        {
            if(weight[k]&&G.matrix[j][k]<weight[k])
                weight[k]=G.matrix[j][k];
        }
    }
    // 計算最小生成樹的權值
    sum = 0;
    for (i = 1; i < index; i++)
    {
        min = INF;
        // 獲取prims[i]在G中的位置
        n = get_position(G, prim[i]);
        // 在vexs[0...i]中，找出到j的權值最小的頂點。
        for (j = 0; j < i; j++)
        {
            m = get_position(G, prim[j]);
            if (G.matrix[m][n]<min)
                min = G.matrix[m][n];
        }
        sum += min;
    }
    printf("PRIM(%c)=%d: ", G.vexs[start], sum);
    for (i = 0; i < index; i++)
        printf("%c ", prim[i]);
    printf("\n");
}

int main()
{
    Graph *pG;
    pG=create_graph();
    print_graph(*pG);
    prim(*pG,0);
}

執行結果：