【資料結構】圖(最短路徑Dijkstra演算法)的JAVA程式碼實現
最短路徑的概念
最短路徑的問題是比較典型的應用問題。在圖中,確定了起始點和終點之後,一般情況下都可以有很多條路徑來連線兩者。而邊或弧的權值最小的那一條路徑就稱為兩點之間的最短路徑,路徑上的第一個頂點為源點,最後一個頂點為終點。
圖的最短路徑的演算法有很多,本文主要介紹狄克斯特拉(Dijkstra)提出的一種按照長度遞增的次序產生的最短路徑的演算法。
Dijkstra演算法介紹
Dijkstra演算法的特點
Dijkstra演算法使用了廣度優先搜尋解決賦權有向圖或者無向圖的單源最短路徑問題,演算法最終得到一個最短路徑樹。該演算法常用於路由演算法或者作為其他圖演算法的一個子模組。
該演算法的時間複雜度是n的平方,可以使用堆優化。
但是,要注意一點,Dijkstra演算法只能適用於權值為正的情況下;如果權值存在負數,則不能使用。
Dijkstra演算法的思想
- 設定兩個頂點集S和T,集合S中存放已經找到最短路徑的頂點,集合T中存放著當前還未找到最短路徑的頂點;
- 初始狀態下,集合S中只包含源點V1,T中為除了源點之外的其餘頂點,此時源點到各頂點的最短路徑為兩個頂點所連的邊上的權值,如果源點V1到該頂點沒有邊,則最小路徑為無窮大;
- 從集合T中選取到源點V1的路徑長度最短的頂點Vi加入到集合S中;
- 修改源點V1到集合T中剩餘頂點Vj的最短路徑長度。新的最短路徑長度值為Vj原來的最短路徑長度值與頂點Vi的最短路徑長度加上Vi到Vj的路徑長度值中的較小者;
- 不斷重複步驟3、4,直至集合T的頂點全部加入到集合S中。
Dijkstra演算法的例項演示
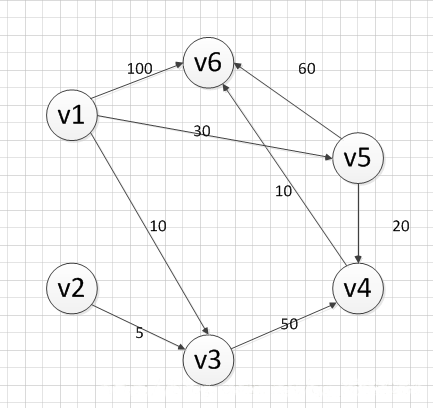
下面求下圖,從源點v1到其他各個頂點的最短路徑:
首先第一步,我們先宣告一個dis陣列(這是一個距離陣列,用於記錄各點距離源點的距離),該陣列初始化的值為:
我們的頂點集T的初始化為:T={v1}。
既然是求 v1頂點到其餘各個頂點的最短路程,那就先找一個離 1 號頂點最近的頂點。通過陣列 dis 可知當前離v1頂點最近是 v3頂點。當選擇了 2 號頂點後,dis[2](下標從0開始)的值就已經從“估計值”變為了“確定值”,即 v1頂點到 v3頂點的最短路程就是當前 dis[2]值。將V3加入到T中。
為什麼呢?因為目前離 v1頂點最近的是 v3頂點,並且這個圖所有的邊都是正數,那麼肯定不可能通過第三個頂點中轉,使得 v1頂點到 v3頂點的路程進一步縮短了。
OK,既然確定了一個頂點的最短路徑,下面我們就要根據這個新入的頂點V3會有出度,發現以v3 為弧尾的有: < v3,v4 >,那麼我們看看路徑:v1–v3–v4的長度是否比v1–v4短,其實這個已經是很明顯的了,因為dis[3]代表的就是v1–v4的長度為無窮大,而v1–v3–v4的長度為:10+50=60,所以更新dis[3]的值,得到如下結果:
因此 dis[3]要更新為 60。這個過程有個專業術語叫做“鬆弛”。即 v1頂點到 v4頂點的路程即 dis[3],通過 < v3,v4> 這條邊鬆弛成功。這便是 Dijkstra 演算法的主要思想:通過“邊”來鬆弛v1頂點到其餘各個頂點的路程。
然後,我們又從除dis[2]和dis[0]外的其他值中尋找最小值,發現dis[4]的值最小,通過之前是解釋的原理,可以知道v1到v5的最短距離就是dis[4]的值,然後,我們把v5加入到集合T中,然後,考慮v5的出度是否會影響我們的陣列dis的值,v5有兩條出度:< v5,v4>和 < v5,v6>,然後我們發現:v1–v5–v4的長度為:50,而dis[3]的值為60,所以我們要更新dis[3]的值.另外,v1-v5-v6的長度為:90,而dis[5]為100,所以我們需要更新dis[5]的值。更新後的dis陣列如下圖:
然後,繼續從dis中選擇未確定的頂點的值中選擇一個最小的值,發現dis[3]的值是最小的,所以把v4加入到集合T中,此時集合T={v1,v3,v5,v4},然後,考慮v4的出度是否會影響我們的陣列dis的值,v4有一條出度:< v4,v6>,然後我們發現:v1–v5–v4–v6的長度為:60,而dis[5]的值為90,所以我們要更新dis[5]的值,更新後的dis陣列如下圖:
然後,我們使用同樣原理,分別確定了v6和v2的最短路徑,最後dis的陣列的值如下:
因此,從圖中,我們可以發現v1-v2的值為:∞,代表沒有路徑從v1到達v2。所以我們得到的最後的結果為:
起點 終點 最短路徑 長度
v1 v2 無 ∞
v3 {v1,v3} 10
v4 {v1,v5,v4} 50
v5 {v1,v5} 30
v6 {v1,v5,v4,v6} 60由此分析下來,我們可以得到以下幾點:
1、需要設立兩個陣列,一個數組為diatance,用於存放個頂點距離源點的距離;另一個數組為st,用於判斷頂點是在哪一個集合內(true為在S集合,false為在T集合內)。
2、Dijkstra演算法的精髓:
- 每次迴圈都將T集合內距離源點最近的那個點加入到S集合中,且加入的那個點距離源點的距離由“最短距離估計值”轉變成“最短距離準確值”;
- 每次迴圈新增一個點到S集合中後,會導致與加入的那個點相鄰的頂點可能會發生距離的更新,也就是“最短距離估計值”的更新。更新方法是取原本的“最短距離估計值”與新加入的那個點的“最短距離確定值”+新加入的那個點與其鄰點的距離的較小者。
- “最短距離估計值”的真正內涵:其實可以把S集合看成一個黑箱子,“最短距離估計值”就是該頂點經過黑箱子裡的各個點到源點的最短距離,但不能保證該頂點是否可以通過黑箱子外(T集合)的頂點繞路達到更短。只有每次迴圈中“最短距離估計值”中的最小值,才能確定為“最短距離確定值”加入到集合S。
Dijkstra演算法的Java程式碼實現
基於鄰接矩陣的程式碼實現:
public int[] dijkstra(int v) {
if (v < 0 || v >= numOfVexs)
throw new ArrayIndexOutOfBoundsException();
boolean[] st = new boolean[numOfVexs];// 預設初始為false
int[] distance = new int[numOfVexs];// 存放源點到其他點的矩離
for (int i = 0; i < numOfVexs; i++)
for (int j = i + 1; j < numOfVexs; j++) {
if (edges[i][j] == 0) {
edges[i][j] = Integer.MAX_VALUE;
edges[j][i] = Integer.MAX_VALUE;
}
}
for (int i = 0; i < numOfVexs; i++) {
distance[i] = edges[v][i];
}
st[v] = true;
// 處理從源點到其餘頂點的最短路徑
for (int i = 0; i < numOfVexs; ++i) {
int min = Integer.MAX_VALUE;
int index=-1;
// 比較從源點到其餘頂點的路徑長度
for (int j = 0; j < numOfVexs; ++j) {
// 從源點到j頂點的最短路徑還沒有找到
if (st[j]==false) {
// 從源點到j頂點的路徑長度最小
if (distance[j] < min) {
index = j;
min = distance[j];
}
}
}
//找到源點到索引為index頂點的最短路徑長度
if(index!=-1)
st[index] = true;
// 更新當前最短路徑及距離
for (int w = 0; w < numOfVexs; w++)
if (st[w] == false) {
if (edges[index][w] != Integer.MAX_VALUE
&& (min + edges[index][w] < distance[w]))
distance[w] = min + edges[index][w];
}
}
return distance;
}基於鄰接表的程式碼實現:
public int[] dijkstra(int v) {
if (v < 0 || v >= numOfVexs)
throw new ArrayIndexOutOfBoundsException();
boolean[] st = new boolean[numOfVexs];// 預設初始為false
int[] distance = new int[numOfVexs];// 存放源點到其他點的距離
for (int i = 0; i < numOfVexs; i++) {
distance[i] = Integer.MAX_VALUE;
}
ENode current;
current = vexs[v].firstadj;
while (current != null) {
distance[current.adjvex] = current.weight;
current = current.nextadj;
}
distance[v] = 0;
st[v] = true;
// 處理從源點到其餘頂點的最短路徑
for (int i = 0; i < numOfVexs; i++) {
int min = Integer.MAX_VALUE;
int index = -1;
// 比較從源點到其餘頂點的路徑長度
for (int j = 0; j < numOfVexs; j++) {
// 從源點到j頂點的最短路徑還沒有找到
if (st[j] == false) {
// 從源點到j頂點的路徑長度最小
if (distance[j] < min) {
index = j;
min = distance[j];
}
}
}
// 找到源點到索引為index頂點的最短路徑長度
if (index != -1)
st[index] = true;
// 更新當前最短路徑及距離
for (int w = 0; w < numOfVexs; w++)
if (st[w] == false) {
current = vexs[w].firstadj;
while (current != null) {
if (current.adjvex == index)
if ((min + current.weight) < distance[w]) {
distance[w] = min + current.weight;
break;
}
current = current.nextadj;
}
}
}
return distance;
}關於演算法程式的兩點說明:
- 這邊方法一個引數是表明了源點的位置,方法的內部會找出從源點到圖中每個點的路徑最小值;
相關推薦
【資料結構】圖(最短路徑Dijkstra演算法)的JAVA程式碼實現
最短路徑的概念最短路徑的問題是比較典型的應用問題。在圖中,確定了起始點和終點之後,一般情況下都可以有很多條路徑來連線兩者。而邊或弧的權值最小的那一條路徑就稱為兩點之間的最短路徑,路徑上的第一個頂點為源點,最後一個頂點為終點。圖的最短路徑的演算法有很多,本文主要介紹狄克斯特拉(
【資料結構】單源最短路徑 Dijkstra演算法
單源最短路徑問題是指:對於給定的有向網路G=(V,E),求原點V0到其他頂點的最短路徑。 按照長度遞增的順序逐步產生最短路徑的方法,稱為Dijkstra演算法。 該演算法的基本思想: 把圖中的所有頂點分成兩組,第一組包括已確定最短路徑的頂點,初始時只含有一個源點,記為集合S;第
【POJ - 2387】Til the Cows Come Home(最短路徑 Dijkstra演算法)
Til the Cows Come Home 大奶牛很熱愛加班,他和朋友在凌晨一點吃完海底撈後又一個人回公司加班,為了多加班他希望可以找最短的距離回到公司。深圳市裡有N個(2 <= N <= 1000)個公交站,編號分別為1..N。深圳是大城市,公交車整天跑跑跑。公交站1是大奶牛的位置,公司所在
【資料結構】圖(深度優先遍歷、廣度優先遍歷)的JAVA程式碼實現
圖的遍歷是指從圖中的任一頂點出發,對圖中的所有頂點訪問一次並且只訪問一次。圖的遍歷是圖的一種基本操作,圖中的許多其他操作也都是建立在遍歷的基礎之上。在圖中,沒有特殊的頂點被指定為起始頂點,圖的遍歷可以從任何頂點開始。圖的遍歷主要有深度優先搜尋和廣度優先搜尋兩種方式。深度優先搜
【資料結構】堆疊(順序棧、鏈棧)的JAVA程式碼實現
堆疊(stack)是一種特殊的線性表,是一種只允許在表的一端進行插入或刪除操作的線性表。表中允許進行插入和刪除操作的一端稱為棧頂,最下面的那一端稱為棧底。棧頂是動態的,它由一個稱為棧頂指標的位置指示器指示。當棧中沒有資料元素時,為空棧。堆疊的插入操作稱為進棧或入棧,堆疊的刪除
紫書第十一章-----圖論模型與演算法(最短路徑Dijkstra演算法Bellman-Ford演算法Floyd演算法)
最短路徑演算法一之Dijkstra演算法 演算法描述:在無向圖 G=(V,E) 中,假設每條邊 E[i] 的長度為 w[i],找到由頂點 V0 到其餘各點的最短路徑。 使用條件:單源最短路徑,適用於邊權非負的情況 結合上圖具體搜尋過程,我繪出下表,方便
單源有權圖的最短路徑 Dijkstra演算法(證明不能解決負權邊)7.1.2
單源最短路徑問題,即在圖中求出給定頂點到其它任一頂點的最短路徑。 Dijkstra演算法 假設存在G=<V,E>,源頂點為0,U={0+已確定的最短路徑頂點},dist[i]記錄頂點0到頂點i的最短距離(包括確定的和估算的),path[i]記錄從0到i路徑上的
圖的最短路徑-Dijkstra演算法和Floyd演算法
Dijkstra演算法 單源點最短路徑問題 Dijkstra演算法主要用來解決單源點最短路徑問題。 給定帶權有向圖G=(V,E),其中每條邊的權是非負數。另外,還給定V中的一個頂點,稱為源。現在要計算從源到所有其他各頂點的最短路徑長度,這裡路徑的長度是指路徑上各邊權之和。這個問題
圖論最短路徑 Dijkstra演算法和模板
Dijkstra演算法是用來求單源最短路徑的演算法。時間複雜度O(N^2); 注意:1,不能求含有負權的圖,含有負權可以採用Bellman-ford和SPFA演算法 2.不能直接求單源最長路徑 演算法思想:把所有的邊分成兩個集合A,B。集合A表示已經求出最短路徑的點,不斷擴充套件集合A,減少集合B
【資料結構】圖的基本操作——圖的構造(鄰接矩陣,鄰接表),遍歷(DFS,BFS)
鄰接矩陣實現如下: /* 主題:用鄰接矩陣實現 DFS(遞迴) 與 BFS(非遞迴) 作者:Laugh 語言:C++ ******************************************* 樣例輸出如下: 請選擇圖的型別(a - 無向圖, b - 有向圖):a 請輸入總頂點
資料結構——帶權有向圖(最短路徑演算法Dijkstra演算法)
Dijkstra演算法是由荷蘭電腦科學家艾茲格·迪科斯徹發現的。演算法解決的是有向圖中最短路徑問題。 舉例來說,如果圖中的頂點表示城市,而邊上的權重表示著城市間開車行經的距離。 Dijkstra演算法可以用來找到兩個城市之間的最短路徑。 Dijkstra演算法的輸入包含了一個有權重的有向圖G,以及G中的一個
【資料結構】圖的構建(鄰接表法)
#include<iostream> #include<string> #include<queue> using namespace std; #define ERROR 1 #define MAX_VERTEX_NUM 100 typedef struct ArcNod
【HDOJ】1874-暢通工程續(最短路徑dijkstra)
amp include using get dijk 找到 間距 距離 ace 1874-暢通工程續 http://acm.hdu.edu.cn/showproblem.php?pid=1874 題意:略。 思路:最短路dijkstra模板,不過要先要把題裏輸入的把兩點間距
【資料結構】圖的深度優先遍歷 廣度優先遍歷
檔案操作比直接輸入方便許多 #include <stdio.h> #include <stdlib.h> #include <string.h> #define M 20 /*鄰接表的儲存結構*/ typedef struct node /
基礎演算法與資料結構(四)最短路徑——Dijkstra演算法
一般最短路徑演算法習慣性的分為兩種:單源最短路徑演算法和全頂點之間最短路徑。前者是計算出從一個點出發,到達所有其餘可到達頂點的距離。後者是計算出圖中所有點之間的路徑距離。 單源最短路徑 Dijkstra演算法 思維 本質上是貪心的思想,宣告一個數組dis來儲存源點到各個頂點的最短距離和一個儲存已經
【資料結構】C語言最基礎練習:棧的初始化,壓棧,出棧,遍歷,清空
隨手練習一下,詳細程式碼解釋都在程式碼片裡請仔細看看 如果有什麼不對的地方,請在下方留言 先建立標頭檔案: #define _CRT_SECURE_NO_WARNINGS 1 #ifndef _TEST_H #define _TEST_H //棧的鏈式儲存結構;
8、【資料結構】圖之鄰接矩陣、鄰接表無向圖
一、鄰接矩陣無向圖 1、基本定義 #define MAX 10 class MatrixUDG { private: char mVexs[MAX]; //頂點集合 int mVexNum; //頂點
9、【資料結構】圖之鄰接矩陣、鄰接表有向圖
一、鄰接矩陣有向圖 1、基本定義 #define MAX 10 class MatrixDG { private: char mVexs[MAX]; // 頂點集合 int mVexNum; // 頂點數
10、【資料結構】圖之深度優先和廣度優先搜尋
一、深度優先搜尋 1、深度優先搜尋介紹 圖的深度優先搜尋(Depth First Search),和樹的先序遍歷比較類似。 它的思想:假設初始狀態是圖中所有頂點均未被訪問,則從某個頂點v出發,首先訪問該頂點,然後依次從它的各個未被訪問的鄰接點出發
【資料結構】圖的儲存結構
是否可以採用順序儲存結構儲存圖? 圖的特點:頂點之間的關係是m:n,即任何兩個頂點之間都可能存在關係(邊),無法通過儲存位置表示這種任意的邏輯關係,所以,圖無法採用順序儲存結構。 如何儲存圖? 考慮圖的定義,圖是由頂點和邊組成的,分別考慮如何儲存頂點、如何