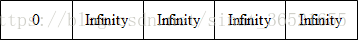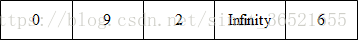圖的最短路徑-Dijkstra演算法和Floyd演算法
Dijkstra演算法
單源點最短路徑問題
Dijkstra演算法主要用來解決單源點最短路徑問題。
給定帶權有向圖G=(V,E),其中每條邊的權是非負數。另外,還給定V中的一個頂點,稱為源。現在要計算從源到所有其他各頂點的最短路徑長度,這裡路徑的長度是指路徑上各邊權之和。這個問題通常稱為單源最短路徑問題(Single-Source Shortest Paths)。
應用例項——計算機網路傳輸:怎樣找到一種最經濟的方式,從一臺計算機向網上所有其它計算機發送一條訊息。
思想
設定一個集合S存放已經找到最短路徑的頂點,S的初始狀態只包含源點v,對vi∈V-S,假設從源點v到vi的有向邊為最短路徑。以後每求得一條最短路徑v, …, vk,就將vk加入集合S中,並將路徑v, …, vk , vi與原來的假設相比較,取路徑長度較小者為最短路徑。重複上述過程,直到集合V中全部頂點加入到集合S中。
資料結構:
圖的儲存結構:帶權的鄰接矩陣。
陣列distance[n]:每個distance[i]記錄源點到各頂點的最小距離。
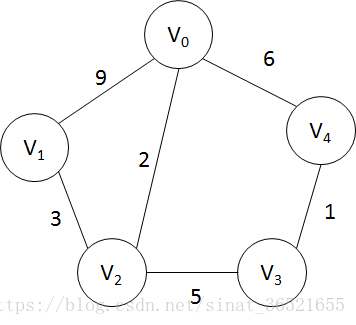
例:
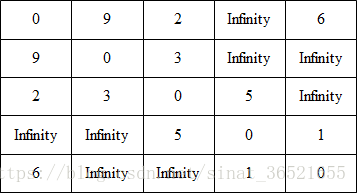
它的鄰接矩陣:
第一步:假設源點為V0,那麼目前最短路徑的頂點集合Q中就只有{V0}和無法到達頂點集合R中有{V1, V2, V3, V4}
第二步:初始化distance陣列,就是下面這樣
第三步:以distance陣列中值為非Infinity的頂點為中轉跳點,這一步就是V0,依照如果distance[V] + matrix[V][W] < distance[W],那麼distance[W] = distance[V] + matrix[V][W]的規則,distance陣列就會變成下面這樣,同時集合Q變成了{V0, V1, V2, V4},集合R變成了{V3}
第四步:因為集合R中還有1個頂點,所以重複第三步的方法,然後變成以V1為中轉跳點,但是以V1為中轉頂點都不滿足distance[V] + matrix[V][W] < distance[W],所以沒更新distance和兩個集合
第五步:因為集合R中還有1個頂點,所以重複第三步的方法,此時變成以V2為中轉跳點,然後發現V0到達V3的距離可以更新,因為2 + 3 < 9,所以distance更新,集合也更新。
之後同理,遍歷完distance之後,輸出
程式碼
function Dijkstra(matrix, start = 0) { const rows = matrix.length,//rows和cols一樣,其實就是頂點個數 cols = matrix[0].length; if(rows !== cols || start >= rows) return new Error("鄰接矩陣錯誤或者源點錯誤"); //初始化distance const distance = new Array(rows).fill(Infinity); distance[start] = 0; for(let i = 0; i < rows; i++) { //達到不了的頂點不能作為中轉跳點 if(distance[i] < Infinity) { for(let j = 0; j < cols; j++) { //比如通過比較distance[i] + matrix[i][j]和distance[j]的大小來決定是否更新distance[j]。 if(matrix[i][j] + distance[i] < distance[j]) { distance[j] = matrix[i][j] + distance[i]; } } console.log(distance); } } return distance; } /** * 鄰接矩陣 * 值為頂點與頂點之間邊的權值,0表示無自環,一個大數表示無邊(比如10000) * */ const MAX_INTEGER = Infinity;//沒有邊或者有向圖中無法到達 const MIN_INTEGER = 0;//沒有自環 const matrix= [ [MIN_INTEGER, 9, 2, MAX_INTEGER, 6], [9, MIN_INTEGER, 3, MAX_INTEGER, MAX_INTEGER], [2, 3, MIN_INTEGER, 5, MAX_INTEGER], [MAX_INTEGER, MAX_INTEGER, 5, MIN_INTEGER, 1], [6, MAX_INTEGER, MAX_INTEGER, 1, MIN_INTEGER] ];
Floyd演算法
主要用於解決任意兩點間最短路徑問題的演算法。
思想
對於從vi到vj的弧,進行n次試探:首先考慮路徑vi,v0,vj是否存在,如果存在,則比較vi,vj和vi,v0,vj的路徑長度,取較短者為從vi到vj的中間頂點的序號不大於0的最短路徑。在路徑上再增加一個頂點v1,依此類推,在經過n次比較後,最後求得的必是從頂點vi到頂點vj的最短路徑。