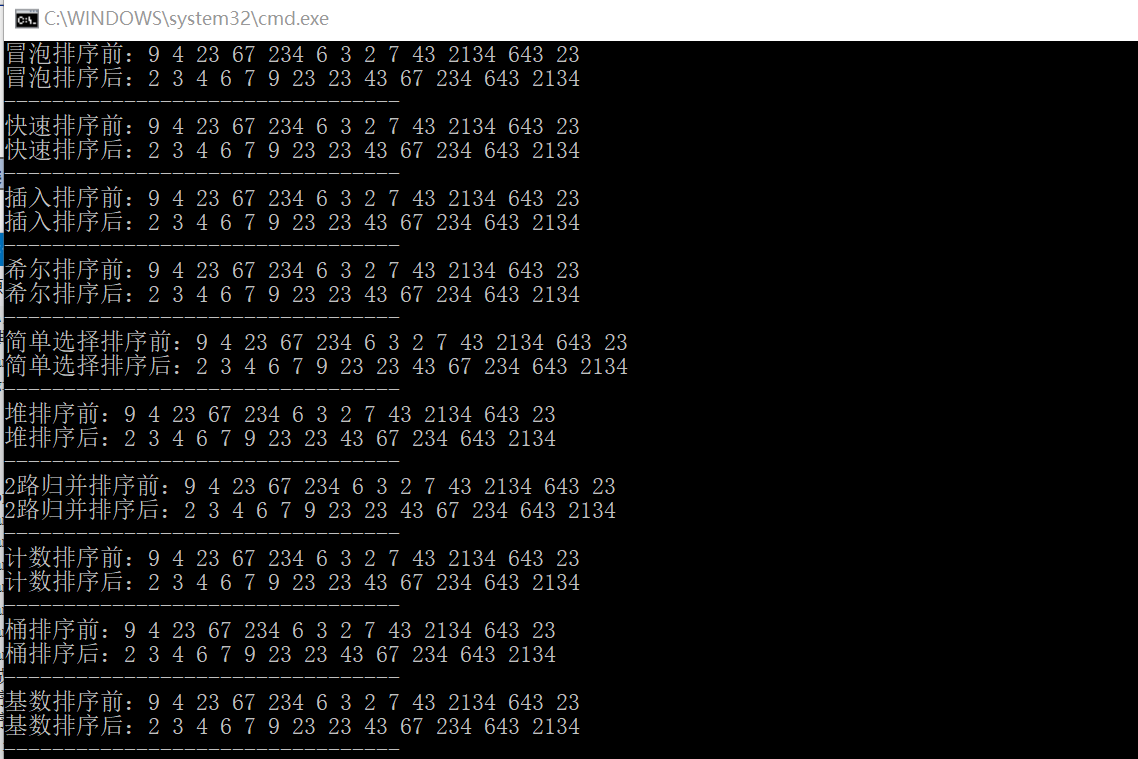
[演算法] 十個經典排序演算法
阿新 • • 發佈:2019-01-11
動圖演示參考:https://www.cnblogs.com/onepixel/articles/7674659.html
基數排序參考:https://blog.csdn.net/double_happiness/article/details/72452243
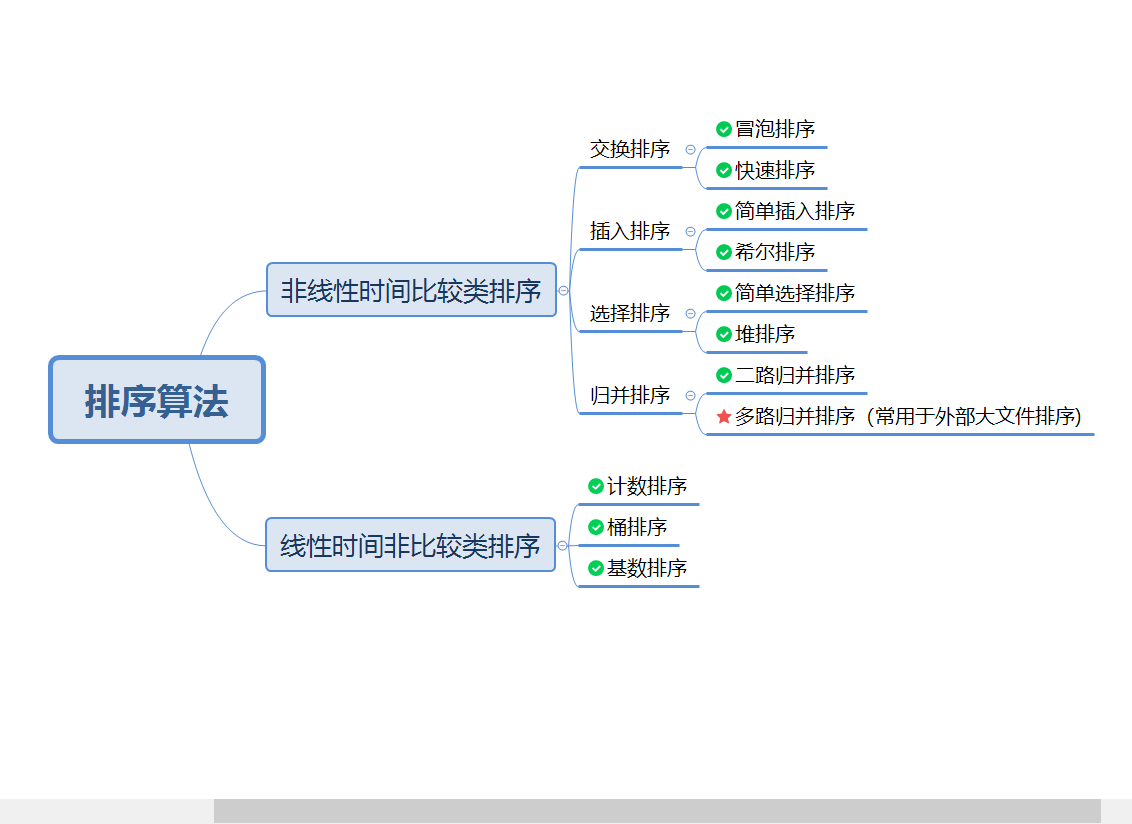
1、常見的排序演算法
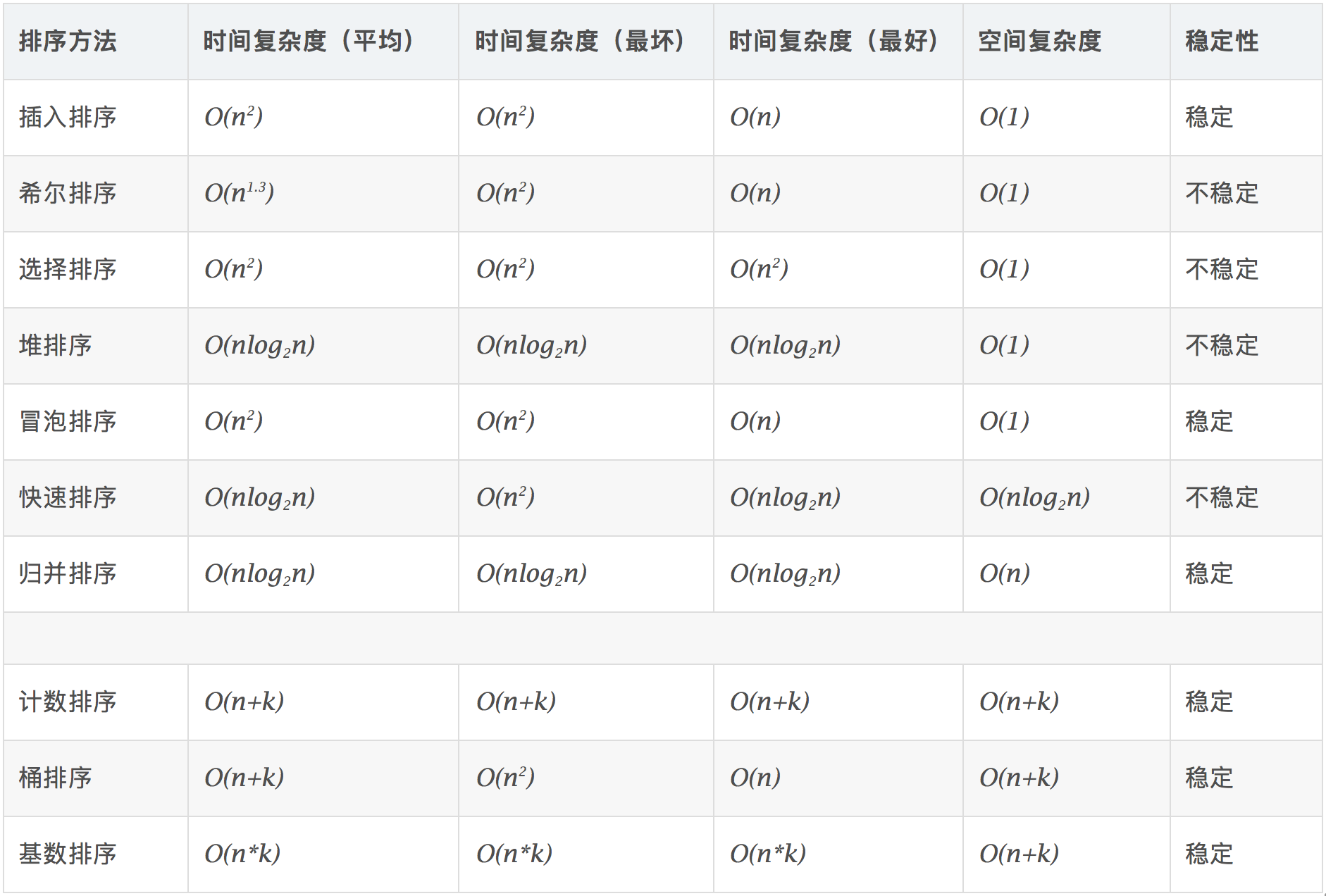
2、演算法分析
3、演算法的實現
1)排序類
1 #ifndef _SORT_H_ 2 #define _SORT_H_ 3 4 #include<vector> 5 6 class Sort { 7 public: 8 //交換排序:冒泡和快排 9 void bubbleSort(std::vector<int> &nums); 10 void quickSort(std::vector<int> &nums, int left, int right); 11 12 //插入排序:簡單插入和希爾排序 13 void insertSort(std::vector<int>&nums); 14 void shellSort(std::vector<int>&nums); 1516 //選擇排序:簡單選擇排序和堆排序 17 void selectSort(std::vector<int>&nums); 18 void heapSort(std::vector<int>&nums); 19 20 //歸併排序:二路歸併和多路歸併 21 void mergeSort2(std::vector<int>&,int,int); 22 23 //計數排序 24 void countingSort(std::vector<int>&); 25//桶排序——計數排序的進階版 26 void bucketSort(std::vector<int>&); 27 //基數排序 28 void RadixSort(std::vector<int>&nums); 29 private: 30 void swap_ele(int &a, int &b) { 31 int tmp = a; 32 a = b; 33 b = tmp; 34 } 35 }; 36 37 #endif // !_SORT_H_
2)排序演算法的具體實現
1 /** 2 * 氣泡排序是一種簡單的排序演算法。 3 * 它重複地走訪過要排序的數列,一次比較兩個元素,如果它們的順序錯誤就把它們交換過來。 4 * 走訪數列的工作是重複地進行直到沒有再需要交換,也就是說該數列已經排序完成。 5 * 這個演算法的名字由來是因為越小的元素會經由交換慢慢“浮”到數列的頂端。 6 * 時間複雜度n*n 7 * 穩定性:穩定 8 */ 9 void Sort::bubbleSort(std::vector<int>&nums) { 10 for (int i = 0; i < nums.size() - 1; ++i) { 11 for (int j = 0; j < nums.size() - 1 - i; ++j) { 12 if (nums[j] > nums[j + 1]) 13 swap_ele(nums[j], nums[j + 1]); 14 } 15 } 16 } 17 18 /** 19 * 快速排序 20 * 通過一趟排序將待排記錄分隔成獨立的兩部分,其中一部分記錄的關鍵字均比另一部分的關鍵字小, 21 * 則可分別對這兩部分記錄繼續進行排序,以達到整個序列有序。 22 * 利用了分治的思想 23 * 時間複雜度 n*logn 24 * 穩定性:不穩定 25 */ 26 void Sort::quickSort(std::vector<int> &nums, int left, int right) { 27 if (left >= right) 28 return; 29 int i = left, j = right; 30 int base = nums[left]; 31 while (i < j) { 32 while (i<j&&nums[j]>=base)//注意等號 33 --j; 34 if (i < j) 35 nums[i] = nums[j]; 36 while (i < j&&nums[i] <= base)//注意等號 37 ++i; 38 if (i < j) 39 nums[j] = nums[i]; 40 } 41 nums[i] = base; 42 quickSort(nums, left, i - 1); 43 quickSort(nums, i + 1, right); 44 } 45 46 /** 47 * 插入排序 48 * 從第一個元素開始,該元素可以認為已經被排序; 49 * 取出下一個元素,在已經排序的元素序列中從後向前掃描; 50 * 如果該元素(已排序)大於新元素,將該元素移到下一位置; 51 * 重複步驟3,直到找到已排序的元素小於或者等於新元素的位置; 52 * 將新元素插入到該位置後; 53 * 重複步驟2~5。 54 * 時間複雜度n*n 55 * 穩定性:穩定 56 */ 57 void Sort::insertSort(std::vector<int>&nums) { 58 int tmp,pos; 59 for (int i = 1; i < nums.size(); ++i) { 60 tmp = nums[i]; 61 pos = i - 1; 62 while (pos >= 0 && nums[pos] > tmp) { 63 nums[pos + 1] = nums[pos]; 64 --pos; 65 } 66 nums[pos + 1] = tmp; 67 } 68 } 69 70 /** 71 * 希爾排序 72 * 希爾排序又叫做縮小增量排序,首先選擇一個增量increment,比較距離差為increment的元素,對他們進行簡單插入排序 73 * 然後縮小增量,直到計算增量為1的情況 74 * 增量的選擇對排序的效果至關重要,希爾提出的是increment/2向下取整,直到incremtn==1,Knuth提出取increment/3+1,直到為1 75 * 我們選用的是Knuth的方法 76 * 時間複雜度低於n*n 77 * 穩定性:有的穩定有的不穩定——不穩定 78 */ 79 void Sort::shellSort(std::vector<int>&nums) { 80 int n = nums.size(); 81 if (n < 2)return; 82 int increment = n / 3 + 1; 83 int tmp,i,j; 84 while (increment > 0) { 85 for ( i = increment; i < n; ++i) { 86 tmp = nums[i]; 87 for (j = i - increment; j >= 0 && nums[j] > tmp; j -= increment) {//簡單插入排序 88 nums[j + increment] = nums[j]; 89 } 90 nums[j + increment] = tmp; 91 } 92 //更新increment 93 if (increment == 1)break;//已經計算過1的情況,全部都有順序了 94 increment = increment / 3 + 1; 95 } 96 } 97 98 /** 99 * 簡單選擇排序 100 * 分成兩部分:已經排序序列和未排序序列,前者初始為空; 101 * 通過掃描,找到為排序序列中的最大或者最小元素,放到未排序序列的起始位置,也是已經排序序列的末尾位置 102 * 時間複雜度為n*n 103 * 穩定性:不穩定 104 */ 105 void Sort::selectSort(std::vector<int>&nums) { 106 int Min, min_pos; 107 int n = nums.size(); 108 for (int i = 0; i < n - 1; ++i) { 109 Min = nums[i]; 110 min_pos = i; 111 for (int j = i + 1; j < n ; ++j) { 112 if (nums[j] < Min) { 113 Min = nums[j]; 114 min_pos = j; 115 } 116 } 117 nums[min_pos] = nums[i]; 118 nums[i] = Min; 119 } 120 } 121 122 /** 123 * 堆排序 124 * 利用堆的特性,父節點一定比子節點大(小),這樣每次取出根節點,就是最大(小)的 125 * 時間複雜度:對於n個節點的堆,對每個元素執行pop()操作,時間複雜度是n*logn 126 * 穩定性:不穩定 127 */ 128 void Sort::heapSort(std::vector<int>&nums) { 129 //首先堆化 130 std::make_heap(nums.begin(), nums.end()); 131 //然後進行排序——排序中用到了pop_heap 132 std::sort_heap(nums.begin(), nums.end()); 133 } 134 135 /** 136 * 2路歸併排序 137 * 採用分治的思想,不斷把序列劃分成兩部分,分別對兩部分進行排序 138 * 然後把兩部分合併成一個完整的有序序列 139 * 時間複雜度:n*logn ??如何計算 140 * 穩定性:穩定 141 */ 142 void Sort::mergeSort2(std::vector<int>&nums, int start, int end) { 143 std::vector<int> tmp_v; 144 if (start < end) { 145 int mid = start + (end - start) / 2; 146 mergeSort2(nums, start, mid); 147 mergeSort2(nums, mid + 1, end); 148 //將結果合併到tmp_v陣列中 149 int i = start, j = mid + 1; 150 while (i <= mid||j <= end) { 151 if (i > mid||(j<=end&& nums[i] > nums[j])) {//注意j的界限的判斷 152 tmp_v.push_back(nums[j++]); 153 } 154 else if (j > end || (i<=mid&&nums[j] >= nums[i])) {//注意等號,這裡就決定了歸併排序是穩定的 155 tmp_v.push_back(nums[i++]); 156 } 157 } 158 //從tmp_v拷貝回nums 159 for (i = start; i <= end; ++i) { 160 nums[i] = tmp_v[i - start]; 161 } 162 } 163 } 164 165 /** 166 * 計數排序 167 * 找出陣列nums中最大的數K,建立輔助陣列V,V的長度是K+1 168 * 遍歷nums,統計nums[i]的出現次數,並填入V[nums[i]]中 169 * 遍歷V,用V的下標i填充nums,直到V[i]為0 170 * 計數排序具有一定的侷限性,首先只能針對整數,並且在最大值不算太大並且序列比較集中的時候效率很高 171 * 最好的時間複雜度n+K,最壞的時間複雜度n+K,平均時間複雜度:n+K 172 * 額外空間複雜度:K,K為最大值 173 * 穩定性:穩定 174 */ 175 void Sort::countingSort(std::vector<int>&nums) { 176 int n = nums.size(); 177 if (n < 2)return; 178 int Max = nums[0]; 179 int i; 180 for (i = 1; i < n; ++i) { 181 if (nums[i] > Max) 182 Max = nums[i]; 183 } 184 std::vector<int>V(Max + 1, 0); 185 for (i = 0; i < n; ++i) { 186 ++V[nums[i]]; 187 } 188 int idx = 0; 189 for (i = 0; i < V.size(); ++i) { 190 while (V[i] > 0) { 191 nums[idx++] = i; 192 --V[i]; 193 } 194 } 195 } 196 197 /** 198 * 桶排序——計數排序的進階版 199 * 思想是將陣列nums中的元素通過對映函式分到數量有限的桶裡 200 * 然後再使用其他的排序演算法把每個桶裡的資料進行排序 201 * 最後把各個桶中的記錄列出來即可得到有序序列 202 * 桶排序的效率取決於兩方面:一是桶的數目儘可能大;二是對映函式儘量能夠使n個數據平均分配 203 * 可以發現,計數排序就是桶排序的特殊情況,桶的數目最大,並且每個桶中只有一個數據的情況 204 * 最好的時間複雜度:有n個桶的時候,每個桶都只有一個元素,不用排序,時間複雜度為n 205 * 最壞的時間複雜度:只有1個桶,這取決於採用的排序方法,時間複雜度是n*n或者n*logn 206 * 平均時間複雜度:假設有k個桶,時間複雜度是n+k 207 * 額外的空間複雜度n 208 * 穩定性:取決於單個桶中採用的排序演算法 209 */ 210 void Sort::bucketSort(std::vector<int>&nums) { 211 int n = nums.size(); 212 if (n < 2)return; 213 int Default_Size = 5; 214 int Max=nums[0], Min=nums[0]; 215 int i; 216 for (i = 1; i < n; ++i) { 217 if (nums[i] > Max) 218 Max = nums[i]; 219 if (nums[i] < Min) 220 Min = nums[i]; 221 } 222 int BucketNum = (Max - Min) / Default_Size + 1; 223 std::vector<std::vector<int>>buckets(BucketNum); 224 225 for (i = 0; i < n; ++i) { 226 //對映函式採用(nums[i]-Min)/Default_Size 227 buckets[(nums[i] - Min) / Default_Size].push_back(nums[i]); 228 } 229 //對每個桶中的元素進行快速排序 230 int j; 231 for (j = 0; j < buckets.size(); ++j) { 232 if(buckets[j].size()>1) 233 quickSort(buckets[j],0,buckets[j].size()-1);//這裡採用的方法決定了桶排序是不是穩定的 234 } 235 //按照順序取出元素 236 int idx = 0; 237 for (j = 0; j < buckets.size(); ++j) { 238 for (i = 0; i < buckets[j].size(); ++i) 239 nums[idx++] = buckets[j][i]; 240 } 241 } 242 243 /** 244 * 基數排序 245 * 把nums中所有的數的位數看成是相同長度的 246 * 從個位開始比較各個數的大小 247 * 統計出每位出現的次數,然後根據次數計算出起始位置 248 * 根據起始位置,把nums[i]對映到bucket中 249 * 用bucket的結果覆蓋nums,計算更高位 250 * 時間複雜度 n 251 * 額外的空間 n 252 * 穩定性:穩定 253 */ 254 255 void Sort::RadixSort(std::vector<int>&nums) { 256 int n = nums.size(); 257 if (n < 2)return; 258 int Max = nums[0]; 259 int i; 260 for (i = 0; i < n; ++i) { 261 if (nums[i] > Max) 262 Max = nums[i]; 263 } 264 std::vector<int>pos(10,0); 265 std::vector<int>bucket(n+1);//桶用來記錄一次排序後的結果 266 int exp = 1,idx=0; 267 while (Max /exp) { 268 for (i = 0; i < n; ++i) { 269 ++pos[(nums[i] / exp) % 10];//pos[i]用來記錄每一位出現的次數 270 } 271 for (i = 1; i < 10; ++i) { 272 pos[i] += pos[i - 1];//這個時候pos[i]記錄的是 當前位是i的數字 在桶中的起始位置,注意是起始位置 273 } 274 for (i = 0; i < n; ++i) {//給nums[i]重新排序 275 idx = (nums[i] / exp) % 10; 276 bucket[pos[idx]++] = nums[i]; 277 //這一步是關鍵 278 //pos[idx]代表當前這一位的數字是idx的起始位置,每次用完起始位置之後,要向後移動 279 //這也決定了基數排序是穩定的 280 } 281 for (i = 1; i <= n; ++i) { 282 nums[i-1] = bucket[i];//重新給nums賦值 283 } 284 if (INT_MAX / exp < 10) {//exp已經到了整數極限 285 break; 286 } 287 exp *= 10;//計算更高位 288 for (i = 0; i < 10; ++i) { 289 pos[i] = 0;//還原pos 290 } 291 } 292 }
3)排序演算法的呼叫
1 template <typename T> 2 void printVector(std::vector<T>nums) { 3 for (int i = 0; i < nums.size(); ++i) { 4 std::cout << nums[i] << " "; 5 } 6 std::cout << std::endl; 7 } 8 int main() 9 { 10 Sort mysort; 11 std::vector<int> nums = { 9,4,23,67,234,6,3,2,7,43,2134,643,23 }; 12 std::vector<int> res; 13 std::cout << "氣泡排序前:"; 14 printVector(nums); 15 std::cout << "氣泡排序後:"; 16 mysort.bubbleSort(nums); 17 printVector(nums); 18 std::cout << "---------------------------------" << std::endl; 19 20 nums= { 9,4,23,67,234,6,3,2,7,43,2134,643,23 }; 21 std::cout << "快速排序前:"; 22 printVector(nums); 23 std::cout << "快速排序後:"; 24 mysort.quickSort(nums,0,nums.size()-1); 25 printVector(nums); 26 std::cout << "---------------------------------" << std::endl; 27 28 nums = { 9,4,23,67,234,6,3,2,7,43,2134,643,23 }; 29 std::cout << "插入排序前:"; 30 printVector(nums); 31 std::cout << "插入排序後:"; 32 mysort.insertSort(nums); 33 printVector(nums); 34 std::cout << "---------------------------------" << std::endl; 35 36 nums = { 9,4,23,67,234,6,3,2,7,43,2134,643,23 }; 37 std::cout << "希爾排序前:"; 38 printVector(nums); 39 std::cout << "希爾排序後:"; 40 mysort.shellSort(nums); 41 printVector(nums); 42 std::cout << "---------------------------------" << std::endl; 43 44 nums = { 9,4,23,67,234,6,3,2,7,43,2134,643,23 }; 45 std::cout << "簡單選擇排序前:"; 46 printVector(nums); 47 std::cout << "簡單選擇排序後:"; 48 mysort.selectSort(nums); 49 printVector(nums); 50 std::cout << "---------------------------------" << std::endl; 51 52 nums = { 9,4,23,67,234,6,3,2,7,43,2134,643,23 }; 53 std::cout << "堆排序前:"; 54 printVector(nums); 55 std::cout << "堆排序後:"; 56 mysort.heapSort(nums); 57 printVector(nums); 58 std::cout << "---------------------------------" << std::endl; 59 60 nums = { 9,4,23,67,234,6,3,2,7,43,2134,643,23 }; 61 std::cout << "2路歸併排序前:"; 62 printVector(nums); 63 std::cout << "2路歸併排序後:"; 64 mysort.mergeSort2(nums,0,nums.size()-1); 65 printVector(nums); 66 std::cout << "---------------------------------" << std::endl; 67 68 nums = { 9,4,23,67,234,6,3,2,7,43,2134,643,23 }; 69 std::cout << "計數排序前:"; 70 printVector(nums); 71 std::cout << "計數排序後:"; 72 mysort.countingSort(nums); 73 printVector(nums); 74 std::cout << "---------------------------------" << std::endl; 75 76 nums = { 9,4,23,67,234,6,3,2,7,43,2134,643,23 }; 77 std::cout << "桶排序前:"; 78 printVector(nums); 79 std::cout << "桶排序後:"; 80 mysort.bucketSort(nums); 81 printVector(nums); 82 std::cout << "---------------------------------" << std::endl; 83 84 nums = { 9,4,23,67,234,6,3,2,7,43,2134,643,23 }; 85 std::cout << "基數排序前:"; 86 printVector(nums); 87 std::cout << "基數排序後:"; 88 mysort.bucketSort(nums); 89 printVector(nums); 90 std::cout << "---------------------------------" << std::endl; 91 92 return 0; 93 }
4)結果