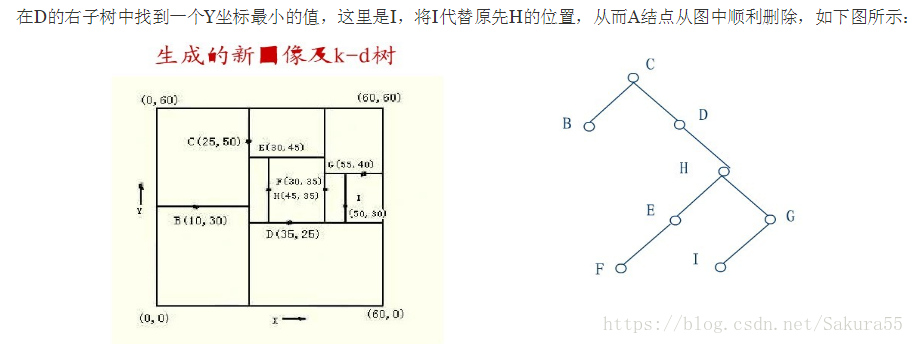
機器學習----KNN中的Kd樹及BBF優化
K最近鄰演算法連結,點選這裡,我們直接來了解有關Kd樹的知識點
一、KD樹基本解釋
1.1、基礎概念
特徵點匹配和資料庫查、影象檢索本質上是同一個問題,都可以歸結為一個通過距離函式在高維向量之間進行相似性檢索的問題,如何快速而準確地找到查詢點的近鄰。
一般說來,索引結構中相似性查詢有兩種基本的方式:
● 一種是範圍查詢,範圍查詢時給定查詢點和查詢距離閾值,從資料集中查詢所有與查詢點距離小於閾值的資料
● 另一種是K近鄰查詢,就是給定查詢點及正整數K,從資料集中找到距離查詢點最近的K個數據,當K=1時,它就是最近鄰查詢。
同樣,針對特徵點匹配也有兩種方法:
最容易的辦法就是線性掃描
另外一種,就是
構建資料索引,因為實際資料一般都會呈現簇狀的聚類形態,因此我們想到建立資料索引,然後再進行快速匹配。索引樹是一種樹結構索引方法,其基本思想是對搜尋空間進行層次劃分。根據劃分的空間是否有混疊可以分為Clipping和Overlapping兩種。前者劃分空間沒有重疊,其代表就是k-d樹如下圖形式的把空間劃分為多個部分的k-d樹。

1.2、什麼是KD樹
Kd-樹就是一種平衡二叉樹k-d樹是一種空間劃分樹,說白了,就是把整個空間劃分為特定的幾個部分,然後在特定空間的部分內進行相關搜尋操作。
1.3、KD樹的構建
下表表示的是Kd-樹中每個節點中主要包含的資料結構:
| 域名 | 資料型別 | 描述 |
|---|---|---|
| Node-data | 資料向量 | 資料集中某個數點,是n維向量(這裡也就是k維) |
| Range | 空間向量 | 該節點所代表的空間範圍 |
| split | 整數 | 垂直於分割超平面的方向軸序號 |
| Left | k-d樹 | 由位於該節點分割超平面左子空間內所有資料點所構成的k-d樹 |
| Right | k-d樹 | 由位於該節點分割超平面右子空間內所有資料點所構成的k-d樹 |
| parent | k-d樹 | 父節點 |
● Range域表示的是節點包含的空間範圍。
● Node-data域就是資料集中的某一個n維資料點。分割超面是通過資料點Node-Data並垂直於軸
● split的平面,分割超面將整個空間分割成兩個子空間。
● 令split域的值為i,如果空間Range中某個資料點的第i維資料小於Node-Data[i],那麼,它就屬於該節點空間的左子空間,否則就屬於右子空間。
● Left,Right域分別表示由左子空間和右子空間空的資料點構成的Kd-樹。
從上面對k-d樹節點的資料型別的描述可以看出構建k-d樹是一個逐級展開的遞迴過程。下面的程式碼構建了kd樹,通過前序遍歷可以進行驗證。
1.3.1、演算法的實現
輸入:資料點集Data-set和其所在的空間Range
輸出:Kd,型別為k-d tree
1、If Data-set為空,則返回空的k-d tree
2、呼叫節點生成程式:
(1)確定split域:對於所有描述子資料(特徵向量),統計它們在每個維上的資料方差。以SURF特徵為例,描述子為64維,可計算64個方差。挑選出最大值,對應的維就是split域的值。資料方差大表明沿該座標軸方向上的資料分散得比較開,在這個方向上進行資料分割有較好的解析度;
(2)確定Node-data域:資料點集Data-set按其第split域的值排序。位於正中間的那個資料點被選為Node-data。此時新的Data-set’ = Data-set\Node-data(除去其中Node-data這一點)。
3、dataleft = {d屬於Data-set’ && d[split] ≤ Node-data[split]}Left_Range = {Range && dataleft} dataright = {d屬於Data-set’ && d[split] > Node-data[split]}Right_Range = {Range && dataright}
4.、eft = 由(dataleft,Left_Range)建立的k-d tree,即遞迴呼叫createKDTree(dataleft,Left_Range)。並設定left的parent域為Kd;right = 由(dataright,Right_Range)建立的k-d tree,即呼叫createKDTree(dataright,Right_Range)。並設定right的parent域為Kd。
1.3.2、構造程式碼部分
# -*- coding: utf-8 -*-
#from operator import itemgetter
import sys
reload(sys)
sys.setdefaultencoding('utf8')
# kd-tree每個結點中主要包含的資料結構如下
class KdNode(object):
def __init__(self, dom_elt, split, left, right):
self.dom_elt = dom_elt # k維向量節點(k維空間中的一個樣本點)
self.split = split # 整數(進行分割維度的序號)
self.left = left # 該結點分割超平面左子空間構成的kd-tree
self.right = right # 該結點分割超平面右子空間構成的kd-tree
class KdTree(object):
def __init__(self, data):
k = len(data[0]) # 資料維度
def CreateNode(split, data_set): # 按第split維劃分資料集exset建立KdNode
if not data_set: # 資料集為空
return None
# key引數的值為一個函式,此函式只有一個引數且返回一個值用來進行比較
# operator模組提供的itemgetter函式用於獲取物件的哪些維的資料,引數為需要獲取的資料在物件中的序號
#data_set.sort(key=itemgetter(split)) # 按要進行分割的那一維資料排序
data_set.sort(key=lambda x: x[split])
split_pos = len(data_set) // 2 # //為Python中的整數除法
median = data_set[split_pos] # 中位數分割點
split_next = (split + 1) % k # cycle coordinates
# 遞迴的建立kd樹
return KdNode(median, split,
CreateNode(split_next, data_set[:split_pos]), # 建立左子樹
CreateNode(split_next, data_set[split_pos + 1:])) # 建立右子樹
self.root = CreateNode(0, data) # 從第0維分量開始構建kd樹,返回根節點
# KDTree的前序遍歷
def preorder(root):
print root.dom_elt
if root.left: # 節點不為空
preorder(root.left)
if root.right:
preorder(root.right)
if __name__ == "__main__":
data = [[2,3],[5,4],[9,6],[4,7],[8,1],[7,2]]
kd = KdTree(data)
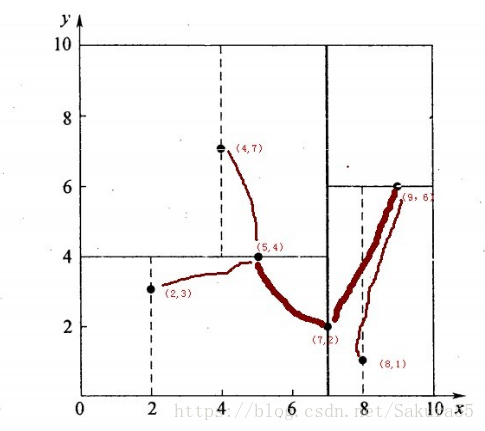
preorder(kd.root)再舉一個簡單直觀的例項來介紹k-d樹構建演算法。假設有6個二維資料點{(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)},資料點位於二維空間內,如下圖所示。為了能有效的找到最近鄰,k-d樹採用分而治之的思想,即將整個空間劃分為幾個小部分,首先,粗黑線將空間一分為二,然後在兩個子空間中,細黑直線又將整個空間劃分為四部分,最後虛黑直線將這四部分進一步劃分。
1.3.2、具體步驟
1、確定:split域=x。具體是:6個數據點在x,y維度上的資料方差分別為39,28.63,所以在x軸上方差更大,故split域值為x;
2、確定:Node-data = (7,2)。具體是:根據x維上的值將資料排序,6個數據的中值(所謂中值,即中間大小的值)為7,所以Node-data域位資料點(7,2)。這樣,該節點的分割超平面就是通過(7,2)並垂直於:split=x軸的直線x=7;
3、確定:左子空間和右子空間。具體是:分割超平面x=7將整個空間分為兩部分:x<=7的部分為左子空間,包含3個節點={(2,3),(5,4),(4,7)};另一部分為右子空間,包含2個節點={(9,6),(8,1)};
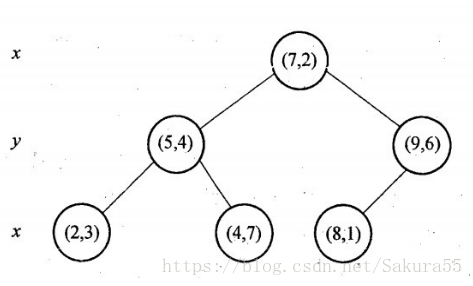
與此同時,經過對上面所示的空間劃分之後,我們可以看出,點(7,2)可以為根結點,從根結點出發的兩條紅粗斜線指向的(5,4)和(9,6)則為根結點的左右子結點,而(2,3),(4,7)則為(5,4)的左右孩子(通過兩條細紅斜線相連),最後,(8,1)為(9,6)的左孩子(通過細紅斜線相連)。如此,便形成了下面這樣一棵k-d樹:
二、KD樹基本操作
2.1、KD樹查詢
KD樹的查詢演算法:
在k-d樹中進行資料的查詢也是特徵匹配的重要環節,其目的是檢索在k-d樹中與查詢點距離最近的資料點。 對於kd樹的檢索,其具體過程為:
● 從根節點開始,將待檢索的樣本劃分到對應的區域中(在kd樹形結構中,從根節點開始查詢,直到葉子節點,將這樣的查詢序列儲存到棧中)
● 以棧頂元素與待檢索的樣本之間的距離作為最短距離min_distance
● 執行出棧操作:
◆ 向上回溯,查詢到父節點,若父節點與待檢索樣本之間的距離小於當前的最短距離min_distance,則替換當前的最短距離min_distance
◆ 以待檢索的樣本為圓心(二維,高維情況下是球心),以min_distance為半徑畫圓,若圓與父節點所在的平面相割,則需要將父節點的另一棵子樹進棧,重新執行以上的出棧操作
● 直到棧為空
舉例
以先前構建好的kd樹為例,查詢目標點(3,4.5)的最近鄰點。同樣先進行二叉查詢,先從(7,2)查詢到(5,4)節點,在進行查詢時是由y = 4為分割超平面的,由於查詢點為y值為4.5,因此進入右子空間查詢到(4,7),形成搜尋路徑:(7,2)→(5,4)→(4,7),取(4,7)為當前最近鄰點。以目標查詢點為圓心,目標查詢點到當前最近點的距離2.69為半徑確定一個紅色的圓。然後回溯到(5,4),計算其與查詢點之間的距離為2.06,則該結點比當前最近點距目標點更近,以(5,4)為當前最近點。用同樣的方法再次確定一個綠色的圓,可見該圓和y = 4超平面相交,所以需要進入(5,4)結點的另一個子空間進行查詢。(2,3)結點與目標點距離為1.8,比當前最近點要更近,所以最近鄰點更新為(2,3),最近距離更新為1.8,同樣可以確定一個藍色的圓。接著根據規則回退到根結點(7,2),藍色圓與x=7的超平面不相交,因此不用進入(7,2)的右子空間進行查詢。至此,搜尋路徑回溯完,返回最近鄰點(2,3),最近距離1.8。
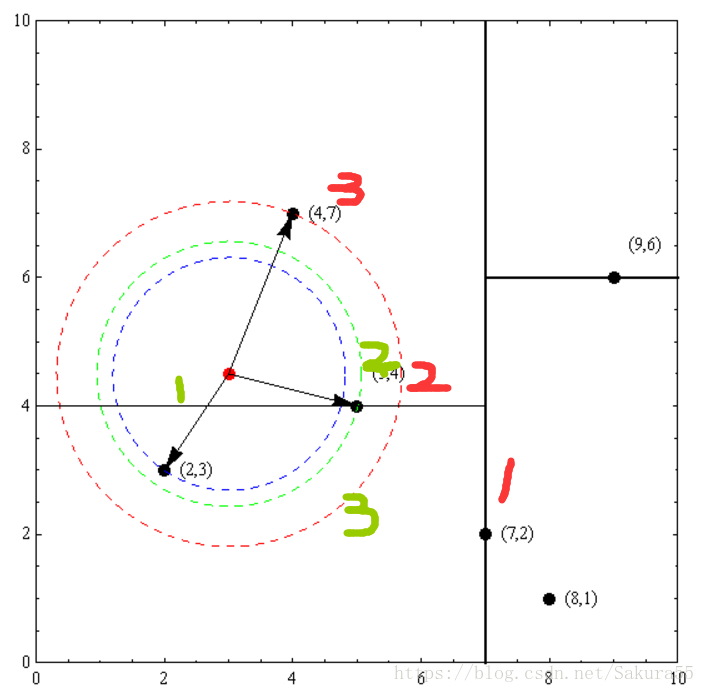
如果例項點是隨機分佈的,kd樹搜尋的平均計算複雜度是O(logN)O(logN),這裡N是訓練例項數。kd樹更適用於訓練例項數遠大於空間維數時的k近鄰搜尋。當空間維數接近訓練例項數時,它的效率會迅速下降,幾乎接近線性掃描。
2.2、查詢程式碼實現
from math import sqrt
from collections import namedtuple
# 定義一個namedtuple,分別存放最近座標點、最近距離和訪問過的節點數
result = namedtuple("Result_tuple", "nearest_point nearest_dist nodes_visited")
def find_nearest(tree, point):
k = len(point) # 資料維度
def travel(kd_node, target, max_dist):
if kd_node is None:
return result([0] * k, float("inf"), 0) # python中用float("inf")和float("-inf")表示正負無窮
nodes_visited = 1
s = kd_node.split # 進行分割的維度
pivot = kd_node.dom_elt # 進行分割的“軸”
if target[s] <= pivot[s]: # 如果目標點第s維小於分割軸的對應值(目標離左子樹更近)
nearer_node = kd_node.left # 下一個訪問節點為左子樹根節點
further_node = kd_node.right # 同時記錄下右子樹
else: # 目標離右子樹更近
nearer_node = kd_node.right # 下一個訪問節點為右子樹根節點
further_node = kd_node.left
temp1 = travel(nearer_node, target, max_dist) # 進行遍歷找到包含目標點的區域
nearest = temp1.nearest_point # 以此葉結點作為“當前最近點”
dist = temp1.nearest_dist # 更新最近距離
nodes_visited += temp1.nodes_visited
if dist < max_dist:
max_dist = dist # 最近點將在以目標點為球心,max_dist為半徑的超球體內
temp_dist = abs(pivot[s] - target[s]) # 第s維上目標點與分割超平面的距離
if max_dist < temp_dist: # 判斷超球體是否與超平面相交
return result(nearest, dist, nodes_visited) # 不相交則可以直接返回,不用繼續判斷
#----------------------------------------------------------------------
# 計算目標點與分割點的歐氏距離
temp_dist = sqrt(sum((p1 - p2) ** 2 for p1, p2 in zip(pivot, target)))
if temp_dist < dist: # 如果“更近”
nearest = pivot # 更新最近點
dist = temp_dist # 更新最近距離
max_dist = dist # 更新超球體半徑
# 檢查另一個子結點對應的區域是否有更近的點
temp2 = travel(further_node, target, max_dist)
nodes_visited += temp2.nodes_visited
if temp2.nearest_dist < dist: # 如果另一個子結點記憶體在更近距離
nearest = temp2.nearest_point # 更新最近點
dist = temp2.nearest_dist # 更新最近距離
return result(nearest, dist, nodes_visited)
return travel(tree.root, point, float("inf")) # 從根節點開始遞迴2.3、KD樹的插入
元素插入到一個K-D樹的方法和二叉檢索樹類似。本質上,在偶數層比較x座標值,而在奇數層比較y座標值。當我們到達了樹的底部,(也就是當一個空指標出現),我們也就找到了結點將要插入的位置。生成的K-D樹的形狀依賴於結點插入時的順序。給定N個點,其中一個結點插入和檢索的平均代價是O(log2N)。
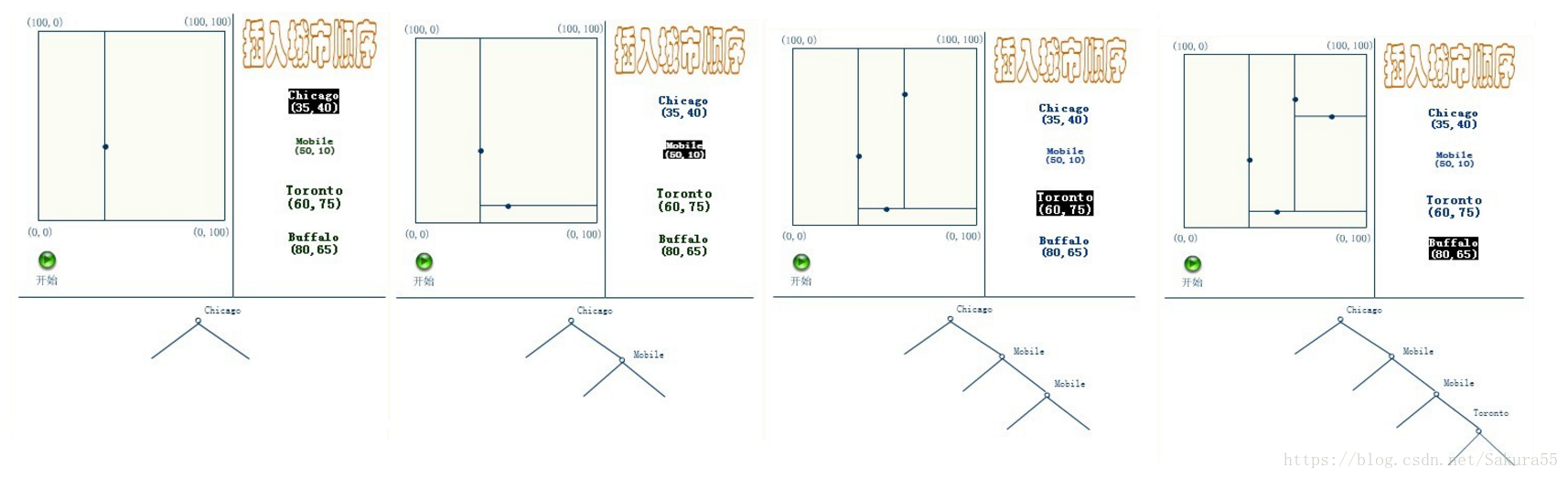
應該清楚,這裡描述的插入過程中,每個結點將其所在的平面分割成兩部分。因比,Chicago 將平面上所有結點分成兩部分,一部分所有的結點x座標值小於35,另一部分結點的x座標值大於或等於35。同樣Mobile將所有x座標值大於35的結點以分成兩部分,一部分結點的Y座標值是小於10,另一部分結點的Y座標值大於或等於10。後面的Toronto、Buffalo也按照一分為二的規則繼續劃分。
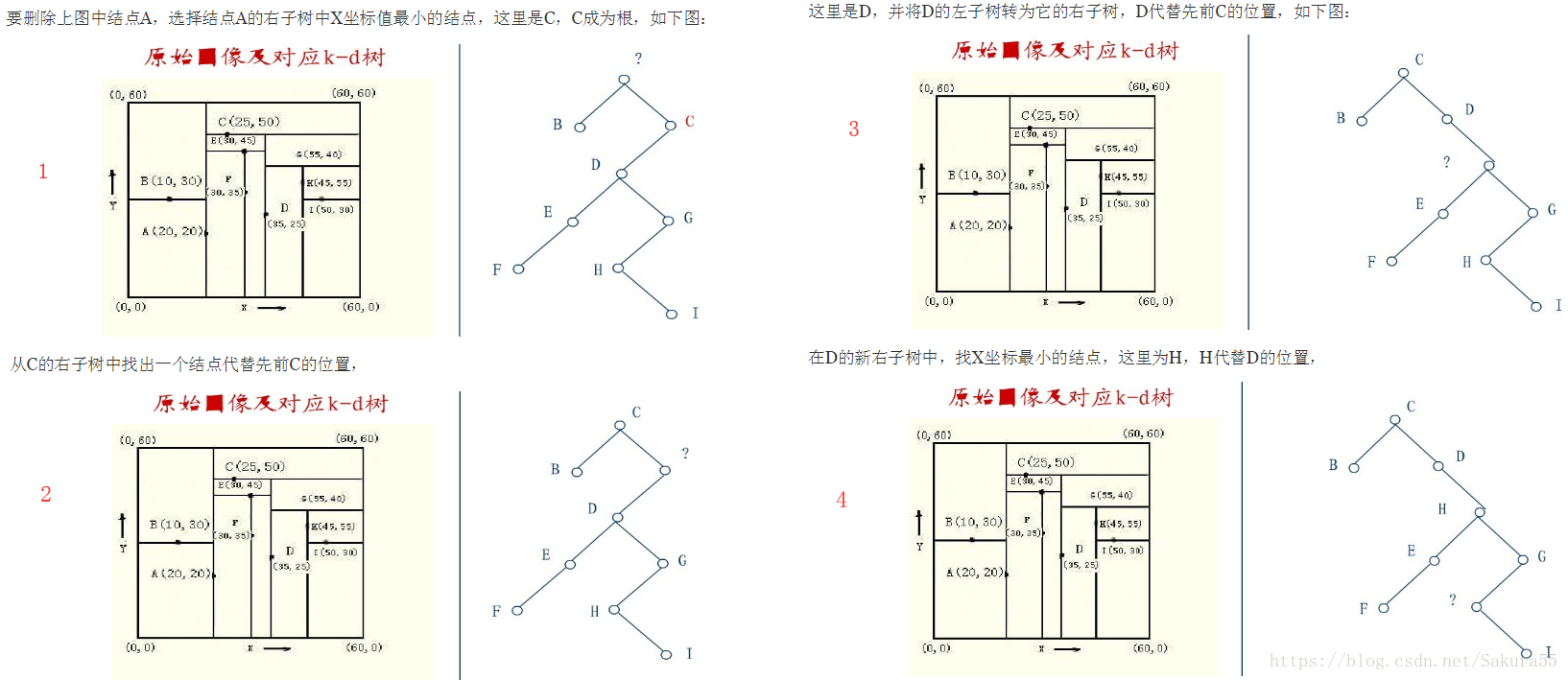
2.4、KD樹的刪除
KD樹的刪除可以用遞迴程式來實現。我們假設希望從K-D樹中刪除結點(a,b)。如果(a,b)的兩個子樹都為空,則用空樹來代替(a,b)。否則,在(a,b)的子樹中尋找一個合適的結點來代替它,譬如(c,d),則遞迴地從K-D樹中刪除(c,d)。一旦(c,d)已經被刪除,則用(c,d)代替(a,b)。假設(a,b)是一個X識別器,那麼,它得替代節點要麼是(a,b)左子樹中的X座標最大值的結點,要麼是(a,b)右子樹中x座標最小值的結點。
具體操作如下:
從一個K-D樹中刪除結點(a,b)的問題變成了在(a,b)的子樹中尋找x座標為最小的結點。不幸的是尋找最小x座標值的結點比二叉檢索樹中解決類似的問題要複雜得多。特別是雖然最小x座標值的結點一定在x識別器的左子樹中,但它同樣可在y識別器的兩個子樹中。因此關係到檢索,且必須注意檢索座標,以使在每個奇數層僅檢索2個子樹中的一個。
從K-D樹中刪除一個結點是代價很高的,很清楚刪除子樹的根受到子樹中結點個數的限制。用TPL(T)表示樹T總的路徑長度。可看出樹中子樹大小的總和為TPL(T)+N。 以隨機方式插入N個點形成樹的TPL是O(N*log2N),這就意味著從一個隨機形成的K-D樹中刪除一個隨機選取的結點平均代價的上界是O(log2N) 。
最終結果如下:
三、演算法改進:BBF
我們在回顧一下KD樹的演算法過程
演算法步驟如下:
● 從根節點開始,將待檢索的樣本劃分到對應的區域中(在kd樹形結構中,從根節點開始查詢,直到葉子節點,將這樣的查詢序列儲存到棧中)
● 以棧頂元素與待檢索的樣本之間的距離作為最短距離min_distance
● 執行出棧操作:
◆ 向上回溯,查詢到父節點,若父節點與待檢索樣本之間的距離小於當前的最短距離min_distance,則替換當前的最短距離min_distance
◆ 以待檢索的樣本為圓心(二維,高維情況下是球心),以min_distance為半徑畫圓,若圓與父節點所在的平面相割,則需要將父節點的另一棵子樹進棧,重新執行以上的出棧操作
● 直到棧為空
當回退到根結點時,搜尋結束,最後的“當前最近點”即為x 的最近鄰點。
如果例項點是隨機分佈的,那麼kd樹搜尋的平均計算複雜度是O(NlogN),這裡的N是訓練例項樹。所以說,kd樹更適用於訓練例項數遠大於空間維數時的k近鄰搜尋,當空間維數接近訓練例項數時,它的效率會迅速下降,一降降到“解放前”:線性掃描的速度。
從上述標準的kd樹查詢過程可以看出其搜尋過程中的“回溯”是由“查詢路徑”決定的,並沒有考慮查詢路徑上一些資料點本身的一些性質。一個簡單的改進思路就是將“查詢路徑”上的結點進行排序,如按各自分割超平面(也稱bin)與查詢點的距離排序,也就是說,回溯檢查總是從優先順序最高(Best Bin)的樹結點開始。
具體步驟和思路如下:
● 在某一層,分割面是第ki維,分割值是kv,那麼 abs(q[ki]-kv) 就是沒有選擇的那個分支的優先順序,也就是計算的是那一維上的距離;
● 同時,從優先佇列裡面取節點只在某次搜尋到葉節點後才發生,計算過距離的節點不會出現在佇列的,比如1~10這10個節點,你第一次搜尋到葉節點的路徑是1-5-7,那麼1,5,7是不會出現在優先佇列的。換句話說,優先佇列裡面存的都是查詢路徑上節點對應的相反子節點,比如:
搜尋左子樹,就把對應這一層的右節點存進佇列。
此演算法能確保優先檢索包含最近鄰點可能性較高的空間,此外,BBF機制還設定了一個執行超時限定。採用了BBF查詢機制後,kd樹便可以有效的擴充套件到高維資料集上。
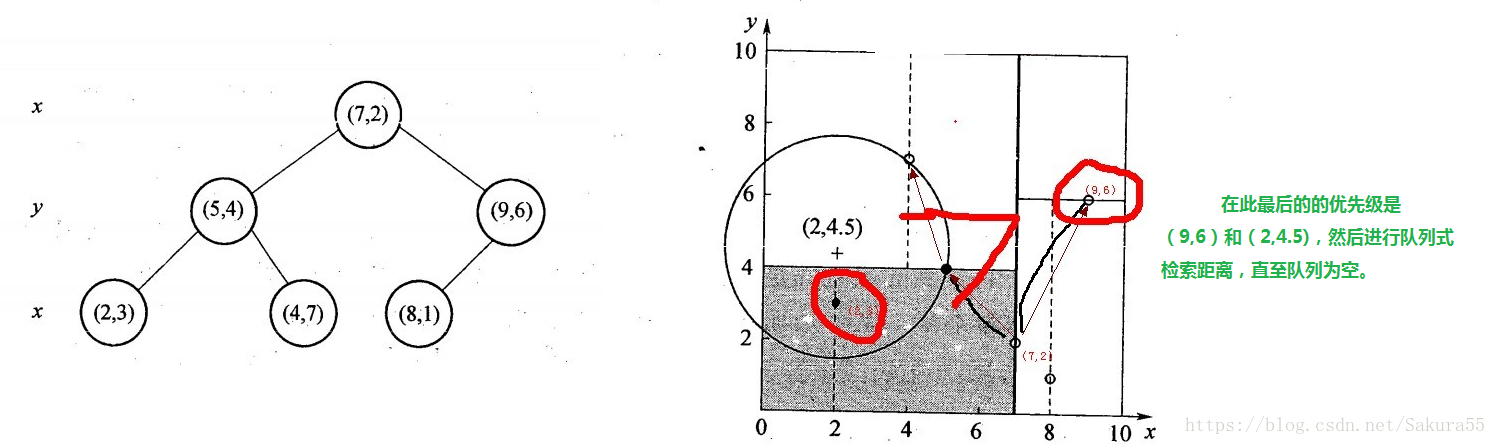
事例
1、將(7,2)壓人優先佇列中;
2、提取優先佇列中的(7,2),由於(2,4.5)位於(7,2)分割超平面的左側,所以檢索其左子結點(5,4)。同時,根據BBF機制”搜尋左/右子樹,就把對應這一層的兄弟結點即右/左結點存進佇列”,將其(5,4)對應的兄弟結點即右子結點(9,6)壓人優先佇列中,此時優先佇列為{(9,6)},最佳點為(7,2);然後一直檢索到葉子結點(4,7),此時優先佇列為{(2,3),(9,6)},“最佳點”則為(5,4);
3、提取優先順序最高的結點(2,3),重複步驟2,直到優先佇列為空。
四、VP樹與MVP樹簡介
高維特徵向量的距離索引問題是基於內容的影象檢索的一項關鍵技術,目前經常採用的解決辦法是首先對高維特徵空間做降維處理,然後採用包括四叉樹、kd樹、R樹族等在內的主流多維索引結構,這種方法的出發點是:目前的主流多維索引結構在處理維數較低的情況時具有比較好的效率,但對於維數很高的情況則顯得力不從心(即所謂的維數危機) 。
實驗結果表明當特徵空間的維數超過20 的時候,效率明顯降低,而視覺化特徵往往採用高維向量描述,一般情況下可以達到10^2的量級,甚至更高。在表示影象視覺化特徵的高維向量中各維資訊的重要程度是不同的,通過降維技術去除屬於次要資訊的特徵向量以及相關性較強的特徵向量,從而降低特徵空間的維數,這種方法已經得到了一些實際應用。
然而這種方法存在不足之處採用降維技術可能會導致有效資訊的損失,尤其不適合於處理特徵空間中的特徵向量相關性很小的情況。另外主流的多維索引結構大都針對歐氏空間,設計需要利用到歐氏空間的幾何性質,而影象的相似性計算很可能不限於基於歐氏距離。這種情況下人們越來越關注基於距離的度量空間高維索引結構可以直接應用於高維向量相似性查詢問題。
相關推薦
機器學習----KNN中的Kd樹及BBF優化
K最近鄰演算法連結,點選這裡,我們直接來了解有關Kd樹的知識點 一、KD樹基本解釋 1.1、基礎概念 特徵點匹配和資料庫查、影象檢索本質上是同一個問題,都可以歸結為一個通過距離函式在高維向量之間進行相似性檢索的問題,如何快速而準確地找到查詢
機器學習筆記之八—— knn-最簡單的機器學習演算法以及KD樹原理
上一節結束了線性迴歸、邏輯迴歸,今天一節來介紹機器學習中最簡單的演算法: K近鄰(KNN,全稱K-nearst Neighbor) 概述:判斷一個樣本的label只需要判斷該樣本週圍其他樣本的label。簡言之,朋
100天搞定機器學習|Day23-25 決策樹及Python實現
演算法部分不再細講,之前發過很多: 【算法系列】決策樹 決策樹(Decision Tree)ID3演算法 決策樹(Decision Tree)C4.5演算法 決策樹(Decision Tree)CART演算法 ID3、C4.5、CART三種決策樹的區別 實驗: 匯入需要用到的python庫 import
【機器學習】梯度下降演算法及梯度優化演算法
用於評估機器學習模型的就是損失函式,我們訓練的目的基本上都是最小化損失,這個最小化的方式就要用優化演算法了,機器學習中最常用的就是梯度下降演算法。 導數、方向導數和梯度 要了解梯度下降演算法是什麼首要知道梯度是什麼,導數和方向導數又是瞭解梯度的前提。
機器學習問題中過擬合出現的原因及解決方案
如果一味的追求模型的預測能力,所選的模型複雜度就會過高,這種現象稱為過擬合。模型表現出來的就是訓練模型時誤差很小,但在測試的時候誤差很大。 一、產生的原因: 1.樣本資料問題 樣本資料太少 樣本抽樣不符合業務場景 樣本中的噪音資料影響 2.模型問題 模型複雜度高,引
kmean、KNN、kd樹的改進演算法BBF
1. k-Means k-Means這裡k的概念是指聚類的k箇中心,聚類成K類,k均值演算法的計算過程非常直觀: 1、從D中隨機取k個元素,作為k個簇的各自的中心。 2、分別計算剩下的元素到k個簇中心的相異度,將這些元素分別劃歸到相異度最低的簇。
機器學習經典演算法詳解及Python實現--決策樹(Decision Tree)
(一)認識決策樹 1,決策樹分類原理 決策樹是通過一系列規則對資料進行分類的過程。它提供一種在什麼條件下會得到什麼值的類似規則的方法。決策樹分為分類樹和迴歸樹兩種,分類樹對離散變數做決策樹,迴歸樹對連續變數做決策樹。 近來的調查表明決策樹也是最經常使用的資料探勘演算法,它
機器學習經典演算法詳解及Python實現--K近鄰(KNN)演算法
轉載http://blog.csdn.net/suipingsp/article/details/41964713 (一)KNN依然是一種監督學習演算法 KNN(K Nearest Neighbors,K近鄰 )演算法是機器學習所有演算法中理論最簡單,最好理解的。KNN
《機器學習實戰》——決策樹的構造及案例
ID3演算法的決策樹的構造 決策樹的理論部分,不再贅述,本篇博文主要是自己的學習筆記(《機器學習實戰》) 先看下述決策樹,希望對理解決策樹有一定的幫助。 3.1.1資訊增益 首先需要了解兩個公式: 建立名為treesde.py檔案,將下述程式碼新增進去 from m
Spark機器學習(6):決策樹算法
projects 信息 txt .cn import n) .com util seq 1. 決策樹基本知識 決策樹就是通過一系列規則對數據進行分類的一種算法,可以分為分類樹和回歸樹兩類,分類樹處理離散變量的,回歸樹是處理連續變量。 樣本一般都有很多個特征,有的特征對分
機器學習入門之決策樹算法
所有 最大的 id3 次數 要去 決策樹算法 4.5 獲取 ddl 1、什麽是決策樹(Decision Tree) 決策樹是一個類似於流程圖的樹結構,其中每一個樹節點表示一個屬性上的測試,每一個分支代表一個屬性的輸出,每一個樹葉節點代 表一個類或者類的分布
機器學習實戰精讀--------決策樹
決策樹 機器學習 python感覺自己像個學走路的孩子,每一步都很吃力和認真!機器根據數據集創建規則,就是機器學習。決策樹:從數據集合中提取一系列規則,適用於探索式的知識發現。決策樹本質:通過一系列規則對數據進行分類的過程。決策樹算法核心:構建精度高,數據規模小的決策樹。ID3算法:此算法目的在於減少樹的深
機器學習-KNN分類器
pos show sha key borde 不同 簡單的 測試 solid 1. K-近鄰(k-Nearest Neighbors,KNN)的原理 通過測量不同特征值之間的距離來衡量相似度的方法進行分類。 2. KNN算法過程 訓練樣本集:樣本集中每個特征值都
機器學習-Python中訓練模型的保存和再使用
ext model job 模型保存 PE dir code pre del 模型保存 BP:model.save(save_dir) SVM: from sklearn.externals import joblib joblib.dump(clf, save_dir)
機器學習 LR中的參數叠代公式推導——極大似然和梯度下降
jpg blog 我們 應該 圖片 最大似然 gpo 機器學習實戰 pos 機器學習 LR中的參數叠代公式推導——極大似然和梯度下降 Logistic本質上是一個基於條件概率的判別模型(DiscriminativeModel)。
機器學習-KNN算法
訓練集 nbsp 線性分類 但是 測試 優點 http 進行 inf 原理 KNN算法,又叫K近鄰算法。就是在訓練集中數據和標簽已知的情況下,輸入測試數據,將測試數據的特征與訓練集中對應的特征進行相互比較,找到訓練集中與之最為相似的前K個數據,則該測試數據對應的類別就是K個
Python機器學習之梯度提升樹
pri () 糾正 ensemble depth del gbrt 1.5 cer #和隨機森林一樣,基於決策樹,采用連續的方式構建樹,深度很小max_depth<5.重要的參數n_estimate和learning_rate,這兩個參數的y作用在於對模型過擬合化得調
機器學習(十二) 決策樹
圖解 通過 rop 監管 運用 一個 系統 分支 對象屬性 決策樹(Decision Tree)是在已知各種情況發生概率的基礎上,通過構成決策樹來求取凈現值的期望值大於等於零的概率,評價項目風險,判斷其可行性的決策分析方法,是直觀運用概率分析的一種圖解法。由於這種決策分支畫
菜鳥之路——機器學習之HierarchicalClustering層次分析及個人理解
features clu 機器 層次 節點類 均值 成了 range n) 這個算法。我個人感覺有點雞肋。最終的表達也不是特別清楚。 原理很簡單,從所有的樣本中選取Euclidean distance最近的兩個樣本,歸為一類,取其平均值組成一個新樣本,總樣本數少1;不斷的重
機器學習之路--決策樹
eve 分析 完成後 保存 not lba 不同 排序 離散 一,引言: 上一章我們講的kNN算法,雖然可以完成很多分類任務,但它最大的缺點是無法給出數據的內在含義,而決策樹的主要優勢就在於數據形式非常容易理解。決策樹算法能夠讀取數據集合,決策樹的一個重要