一說到散列表，大家腦子想到的詞就是：Hashmap、key-value、查詢速度快、增刪速度快等等。確實，在我們平常的學習生活中，散列表是很常見、也是用的很多的資料結構。那麼散列表是怎樣設計出來的，為什麼它既可以和陣列一樣查詢快，又可以和連結串列一樣快增刪，本節讓我們一起了解一下什麼是散列表、什麼是雜湊函式、它究竟是如何設計出來的。

雜湊思想

　　什麼是雜湊思想呢？散列表還有一個英文名叫做Hashtable，也叫做“雜湊表”、“hash表”，hash我們都瞭解，是同過一定的演算法、hash演算法得到一個物件的雜湊值，用來標識物件本身的演算法。

　　我們來舉一個例子，假如有50個同學參加數學競賽，為了能快速方便地找到每一個人，所以每個人都設立一個編號，從1到50，代表50個學生。現在如果我們用程式碼去實現這一功能的話，我們可以將這50個學生放到陣列中去，從陣列下標為1的位置開始，放入編號為1的學生，以此類推，將學生的編號和陣列的下標一一對應，當我們要找第32個學生的時候，直接arr[32]就可以找到這個學生了，這樣，就達成了O(1)的時間複雜度。實際上，這個例子已經用到了雜湊思想，能夠快速地找到我們想找的學生，如果你覺得不夠明顯的話我們可以稍加改造一下。

　　假如，老師說編號這樣太簡單了，無法明顯地表面這個學生的資訊，需要再加上年級、班級這些資訊，變成了6位數字，比如020433，02代表大二年級、04是4班，後兩位還是之前的編號，這樣我們如何儲存學生的編號才能很快地找到對應的學生。

　　思路還是那個思路，儘管6位數字作為陣列的下標過長，我們可以擷取編號的後兩位，來作為陣列的下標，去讀取我們需要的資料。

　　這就是典型的雜湊思想，這裡參賽選手的編號我們稱作鍵（key），用來標識學生，學生本身這個物件我們稱為值（value）。我們把參賽編號對映為陣列下標的對映方法叫做雜湊函式（hash函式），而經過雜湊函式得到的值就叫做雜湊值（hash值）。

　　通過上面的例子我們可以總結到：散列表用的就是陣列支援按照下標訪問資料時時間複雜度為O(1)的特性來實現的高效訪問，當儲存資料時，通過雜湊函式得到陣列的下標然後將資料放入到該位置中去，然後進行讀取。可以看出，散列表的實質是陣列，是一種升級版的陣列。

雜湊函式

　　雜湊函式顧名思義是個函式，用函式表示就是hash(key)。那麼大家想一下，要編寫一個hash函式需要注意哪些問題呢，hash函式需要滿足什麼呢？

　　1. 雜湊值是一個非負整數

　　2. 如果key1 = key2 ，那麼hash(key1) == hash(key2)

　　3. 如果key1 != key2，那麼hash(key1) != hash(key2)

　　解釋一下這三點，第一點很明顯，陣列的下標是從0開始的，肯定是非負的，

  　  第二點，key一樣，他們的hash值也一樣，也是很正確的，因為陣列一個下標只能對應一個值。

　　但是第三點我們卻無法滿足，當兩個key的值不同的時候，他們的hash值不敢保證一定不一樣。即使是著名的MD5、SHA3這些hash演算法，也無法到達這一目的，所以，以陣列構成的散列表，存在著雜湊衝突的問題。並且陣列的長度有限，隨著值的增多，雜湊衝突的概率也會大大增大。

　　我們目前無法找到一個完美地能夠解決hash衝突的辦法，所以，我們為了解決雜湊衝突，提供了以下幾種思路方法。

雜湊衝突

　　剛才我們說到，再完美的hash函式也無法解決雜湊衝突的問題，那麼，我們該如何去解決雜湊衝突的問題呢？常用的解決方法有兩類：開放定址法（open addressing）和連結串列法(chaining)。

1.開放定址法

開放定址法的思想是，如果出現了雜湊衝突，就重新尋找一個空閒的位置去存放該資料，那麼如何去探測空閒位置呢？

這裡，我們說一個比較簡單的線性探測法，比如我們通過雜湊函式計算出了雜湊值為6，但是陣列這個位置已經有資料了，然後我們就從7開始一直往後找，直到找到空閒的位置，然後插入該元素。

但是，這裡我們會遇到一些問題，比如刪除的時候，我們不能單純地把要刪除的位置設定為空，為什麼呢？

因為如果這個資料本來存在，但是因為線性探測法的原因它被安排在了其他位置，當查詢的時候我們會判定它為不存在。這個問題該如何解決呢？

我們可以將刪除的元素，特殊標記為 deleted。當線性探測查詢的時候，遇到標記為deleted的空間時，並不是停下來，而是繼續往下探測。

結論：

大家肯定已經發現了，線性探測法存在很多的問題。當散列表中的資料越來越多的時候，雜湊衝突發生的可能性就會越來越大，空閒的位置會越來越少，查詢的時間就會越來越長。最壞情況下，查詢的效率會退化為O(n)，所以在資料比較多的時候，裝載因子較少的時候才會去使用開發定址法。

什麼是裝載因子呢？

我們用裝載因子來表示散列表的裝滿程度，也就是空閒狀態。公式為：

散列表的裝載因子 = 填入表中的元素個數 / 散列表的長度

裝載因子越大，說明空閒越少，可能發生的衝突越多。

2..連結串列法

連結串列法是跟為常用的解決雜湊衝突的辦法，學java的小朋友們應該都知道，hashmap就是通過連結串列法來解決的hash衝突。

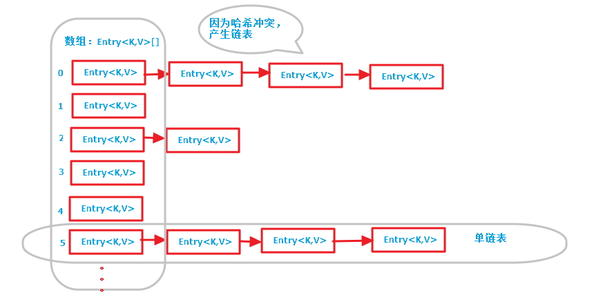
原理很簡單，就是通過雜湊函式得到的目標位置如果已經有資料的話，就形成一個連結串列，將衝突的資料放入連結串列中去，這樣插入的時間複雜度依舊是O(1)，但是當連結串列長度過長的時候，查詢資料的速率會變慢，所以在有些時候，連結串列會轉化為樹來減少查詢的時間。如圖所示，hashmap用連結串列來解決hash衝突

應用場景

 接下來，讓我們看兩個例子，感受一下雜湊表是如何應用的

1.假設我們有 10 萬條 URL 訪問日誌，如何按照訪問次數給URL進行排序

這個問題可以分為兩步，第一步是統計每個URL的訪問次數，第二步根據訪問次數進行排序。那具體怎麼做呢？

首先我們以URL為key，訪問次數為value，存入散列表中。時間O(N)。然後根據訪問次數從大到小排序，用快速排序為O(NlogN)。

2.有兩個字串陣列，每個陣列大約有10萬條字串，如何快速找出兩個陣列中相同的字串？

以第一個字串陣列構建散列表，字串為key，出現次數為value。再遍歷第二個字串陣列，在散列表中查詢，如果value大於0，說明存在該字串，時間複雜度為O（N）

內容小結

今天講了雜湊表一些簡單的構成、設計思想、雜湊函式、雜湊衝突等理論性知識。

散列表是陣列的進化版，利用了陣列支援按照下標快速訪問元素的特性，達到了O(1)的時間複雜度。散列表主要的問題是雜湊衝突問題，常見的兩種方法是開放定址法和連結串列法，其中連結串列法是常用的解決雜湊衝突的方法。

雜湊函式的設計決定了雜湊衝突的概念，也就決定了散列表設計的好壞