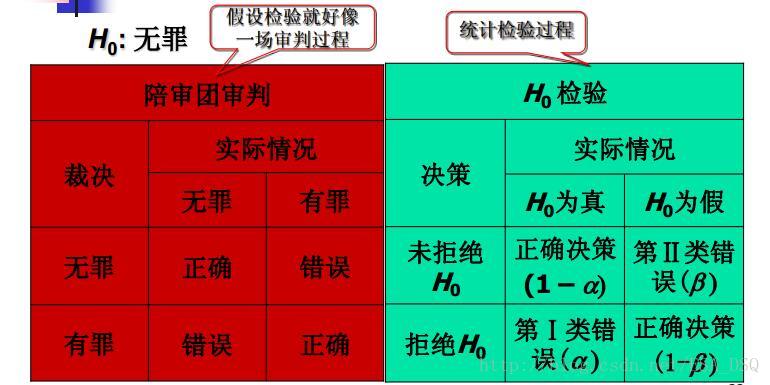
應用統計學與R語言實現學習筆記(六)——假設檢驗
Chapter 6 Hypothesis Test
本篇是第6章,內容是假設檢驗。
1.基本思想
我們還是從問題開始討論。這回提個接地氣的問題——雄安新區批覆前後對該地區房價是否有差異?
嗯,假設檢驗其實就是為了解決這類問題。
假設檢驗的基本思想——我們有樣本,但是無法獲得總體,需要對總體的分佈形式或分佈引數事先作出某種假設,然後根據樣本觀測值,運用統計分析的方法來檢驗這一假設是否正確。
分解開來,假設檢驗=假設+檢驗(或者假設檢驗)。
假設(hypothesis)——對總體的引數的具體數值(或分佈形式)所作的陳述(總體引數包括總體均值、比例、 方差等,分析之前必需陳述)。
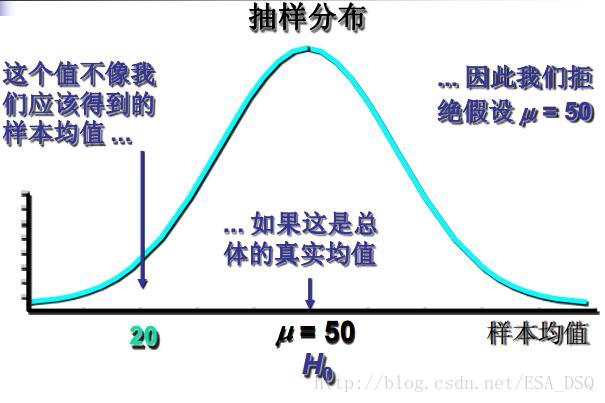
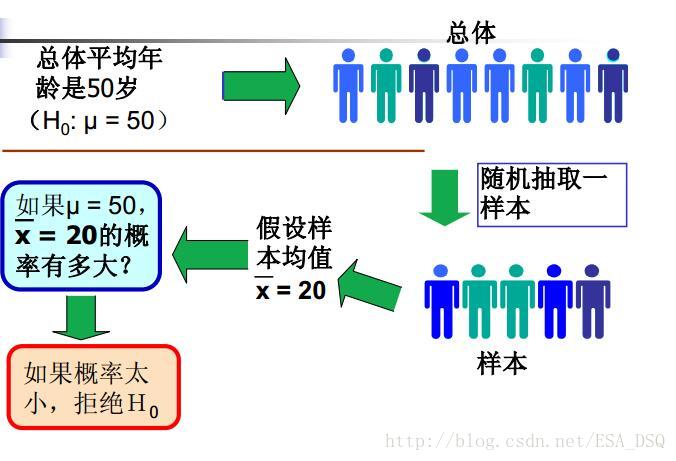
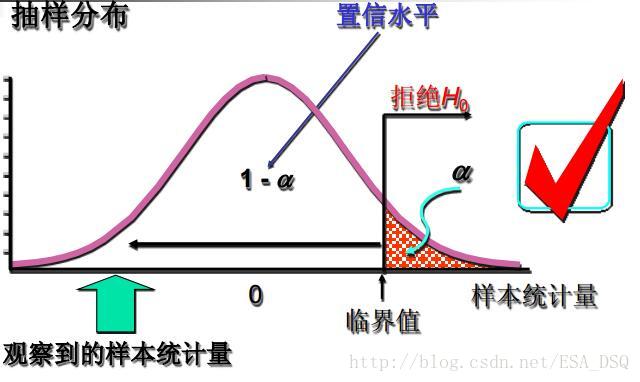
假設檢驗(hypothesis test)—先對總體的引數( 或分佈形式) 提出某種假設,然後利用樣本資訊判斷假設是否成立的過程(有引數檢驗和非引數檢驗;邏輯上運用反證法, 統計上依據小概率原理)。如圖。
假設檢驗的思想還可以去搜索Fisher 顯著性檢驗的思想(女士品茶試驗)的故事深深體會,這裡就不詳述了。有興趣的同學可以點選下文的科學網連結檢視。
2.原假設和備擇假設
從前面的介紹我們知道,假設檢驗的第一步是建立假設。那麼假設分為兩種(原假設和備擇假設)。那麼這二者具體又是什麼呢?
- 原假設(null hypothesis)——原假設又稱“ 0假設”,總是有符號 =, ≥ 或≤,表示為
H0 。是研究者想收集證據予以反對的假設(生產實踐中常對應正常情形,如均值與設計一致);一般來說,原假設是一旦拒絕便要採取行動的假設。因此, 原假設總是“受到保護的假設” ,沒有充分的證據是不能拒絕原假設的。例如,對一家信譽很好的工廠的產品進行檢驗,原假設一般是“ 產品合格”。- 備擇假設(alternative hypothesis)——研究者想收集證據予以支援的假設, 一旦發生就要採取行動, 是與原假設對立的假設,也稱“研究假設”,總是有符號 ≠, > 或 <,表示為
H1 。
總結起來就是,原假設是統計學史上最悲催角色——它從一開始誕生,就是為了被科學家們發好人卡拒絕而存在的一個假設。備擇假設才是科學家們追求的白富美。
搞明白了這兩個假設,下一步我們做假設檢驗的時候,就要先提出假設了,這裡給了一些提出假設的要點:
- 原假設和備擇假設是一個完備事件組, 而且相互對立(在一項假設檢驗中, 原假設和備擇假設必有一個成立, 而且只有一個成立)。
- 先確定備擇假設, 再確定原假設。
- 等號“ =” 總是放在原假設上。
- 因研究目的不同, 對同一問題可能提出不同的假設( 也可能得出不同的結論)。
同時在實際應用中,我們有不同的需求,因此又有雙側檢驗和單側檢驗的區分。
- 雙側檢驗——備擇假設沒有特定的方向性,並含有符號“=”的假設檢驗,稱為雙側檢驗或雙尾檢驗(two-tailed test)
- 單側檢驗——備擇假設具有特定的方向性,並含有符號“>”或“<”的假設檢驗,稱為單側檢驗或單尾檢驗(one-tailed test)。其中備擇假設的方向為“<”,稱為左側檢驗,備擇假設的方向為“>”,稱為右側檢驗。
原假設與備擇假設形式:
- 雙邊檢驗:
H0:μ=2,H1:μ≠2 。- 單邊檢驗:左側檢驗——
H0:μ≤2,H1:μ2 ,右側檢驗——H0:μ≥2,H1:μ<2 。
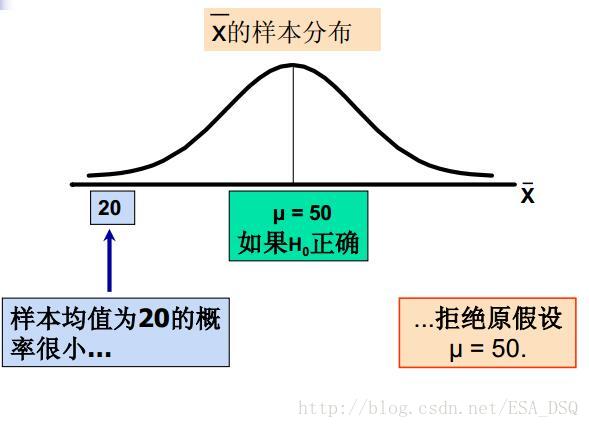
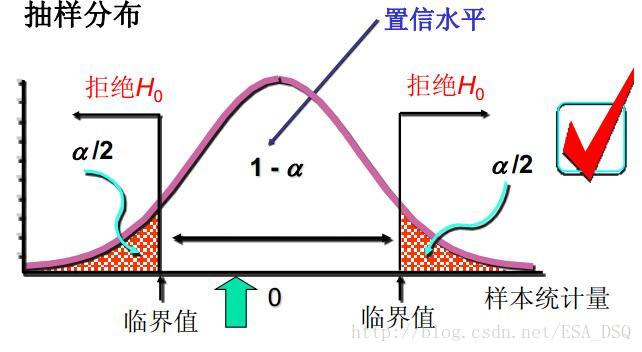
所見即所得,用一張圖來表示假設檢驗過程。
所以拒絕原假設的理由是假設檢驗中的小概率原理。那麼什麼是小概率?
- 在一次試驗中, 一個幾乎不可能發生的事件發生的概率。
- 在一次試驗中小概率事件一旦發生, 我們就有理由拒絕原假設。
- 小概率由研究者事先確定。
所以拒絕
3.第一類錯誤和第二類錯誤
上文介紹了假設檢驗的過程,但是假設檢驗過程會不會出現錯誤呢?其實大家仔細分析拒絕原假設的理由就會發現問題了。通常情況下原假設是小概率事件,但是小概率事件≠0概率事件。小概率事件不是不發生,而是發生概率較小。就像天氣預報說明天有99%的可能不下雨,結果1%的可能性成為了事實,明天下雨了。因此假設檢驗中會有兩類錯誤(棄真錯誤和取偽錯誤)經常出現。
(1)第一類錯誤(棄真錯誤):
- 原假設為真時拒絕原假設。
- 第一類錯誤的概率為α(沒錯,就是它,我們的好朋友,小α。咳咳咳,就是顯著性水平,一般由研究者事先指定,常用的值有0.01, 0.05, 0.10)。
(2)第二類錯誤(取偽錯誤):
- 原假設為假時未拒絕原假設。
- 第二類錯誤的概率記為β。
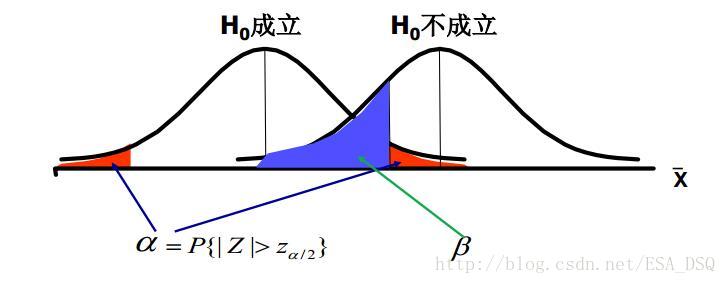
α和β的關係——α和β的關係就像翹翹板, α小β就大,α大β就小。所以兩類錯誤不可能同時發生(第一類只在
影響β的因素:
- 總體引數的真值。
- 顯著性水平α(當α減少時增大)。
- 總體標準差σ(當σ增大時增大)。
- 樣本容量n(當n減少時增大)。
4.統計量與拒絕域
講了這麼多,但是還沒有介紹假設檢驗的計算過程。假設檢驗的過程依賴於兩個重要數學概念(統計量與拒絕域,前面已經有稍微提到了)。這裡再做具體介紹。
檢驗統計量(test statistic)——根據樣本觀測結果計算得到的, 並據以對原假設和備擇假設作出決策的某個樣本統計量,是對樣本估計量的標準化結果(原假設
標準化的檢驗統計量公式為:
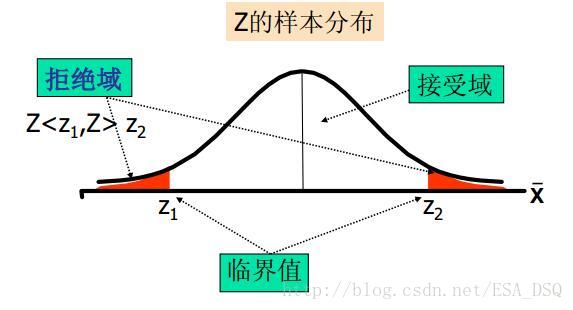
顯著性水平和拒絕域的三種情況:
雙側檢驗:
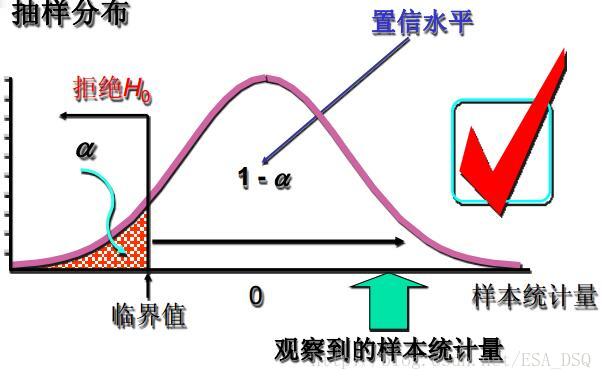
左側檢驗:
右側檢驗:
統計量落在拒絕域時,我們就可以拒絕原假設。具體如下:
- 給定顯著性水平α,查表得出相應的臨界值
zα,zα/2,tα,tα/2,⋯ 。- 將檢驗統計量的值與α水平的臨界值進行比較。
- 作出決策:雙側檢驗——|統計量| > 臨界值,拒絕
H0 ;左側檢驗——統計量 < 臨界值,拒絕H0 ;右側檢驗——統計量 > 臨界值,拒絕H0 。
5.利用p值進行決策
如何利用假設檢驗解決實際問題?很重要的一個應用是在決策上。就如標題說的,利用p值進行決策。那麼什麼是p值?
p值(p-value):在一個假設檢驗問題中,拒絕原假設的最小顯著性水平。
- 在原假設為真的條件下,檢驗統計量的觀察值大於或等於其計算值的概率(雙側檢驗為分佈中檢驗統計量兩側面積的總和;單側檢驗為分佈中檢驗統計量相應單側面積)。
- 反映實際觀測到的資料與原假設
H0 之間的一致程度。- 被稱為觀察到的(或實測的)顯著性水平。
- 決策規則: 若p值<α, 拒絕
H0 。
p值法步驟(以大樣本均值為例)
將樣本統計量轉換成檢驗統計量z
- 計算p值: Z為標準正態分佈隨機變數(
p值=(|Z|≥z)(雙側),p值=(Z≤z)(左側),p值=(Z≥z)(右側) )- 比較p值和α:
如果α≥p值,拒絕H0 ;
如果α< p值,不能拒絕H0 。
假設檢驗結論的表述
假設檢驗的目的就在於試圖找到拒絕原假設的證據, 而不在於證明什麼是正確的。
- 拒絕原假設時結論是清楚的。
- 當不拒絕原假設時——並未給出明確的結論,不能說原假設是正確的, 也不能說它不是正確的。但也未說它不是10。 我們只能說樣本提供的證據還不足以推翻原假設。
假設檢驗步驟的總結
- 陳述原假設和備擇假設。
- 從所研究的總體中抽出一個隨機樣本。
- 確定一個適當的檢驗統計量, 並利用樣本資料算出其具體數值。
- 確定一個適當的顯著性水平, 並計算出其臨界值, 指定拒絕域。
- 將統計量的值與臨界值進行比較, 作出決策——統計量的值落在拒絕域,拒絕
H0 ,否則不拒絕H0 ,也可以直接利用p值作出決策。
6.一個總體引數的檢驗
前面的理論講的差不多了,又到了典型總體引數的檢驗內容的介紹了。依舊是先一個總體引數的檢驗(總體均值、總體比例、總體方差)。
總體均值的檢驗(大樣本: n≥30)
使用z檢驗統計量: