Chapter 14 Case and Practice

本篇是第十四章，內容是案例與實踐。這裡其實是對我公選課的作業做了個彙總。

1 描述性統計與抽樣分佈

1.一種袋裝食品用生產線自動裝填，每袋重量大約為50g，但由於某些原因，每袋重量不會恰好是50g。下面是隨機抽取的100袋食品，測得的重量資料見附錄。
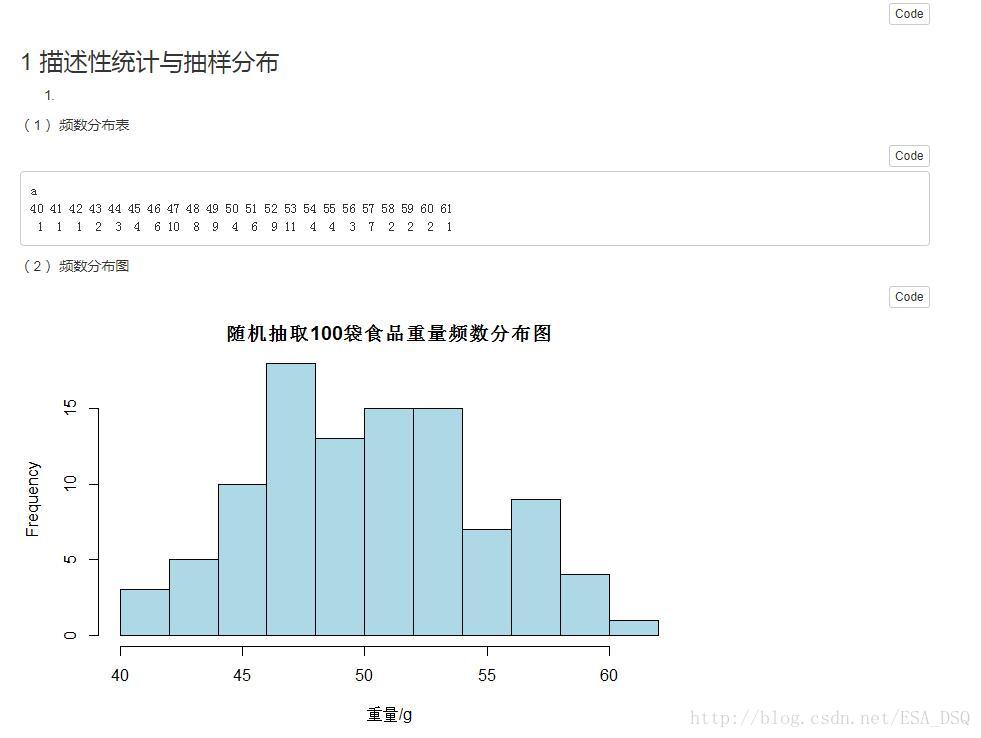
（1）構建這些資料的頻數分佈表。
（2）繪製頻數分佈的直方圖。
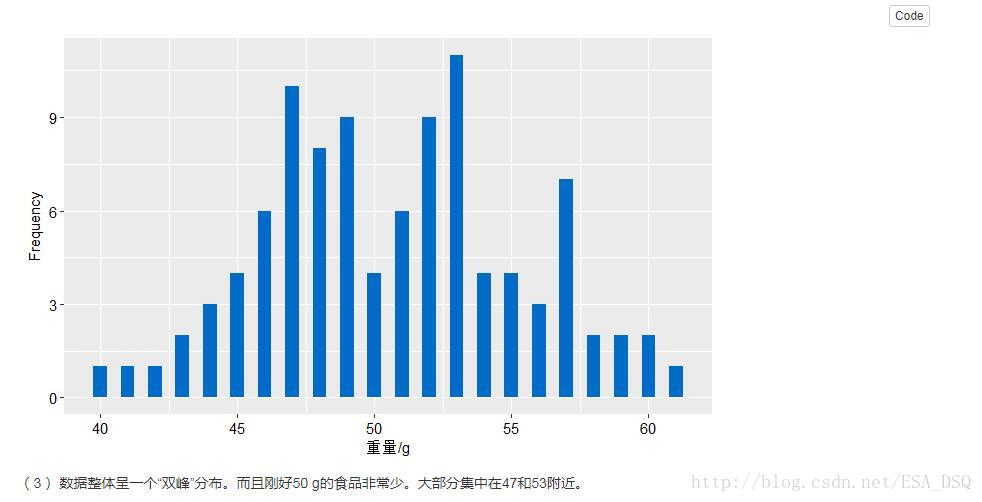
（3）說明資料分佈的特徵。

2.甲乙兩個班各有40名學生，期末統計學考試成績的分佈見附錄。
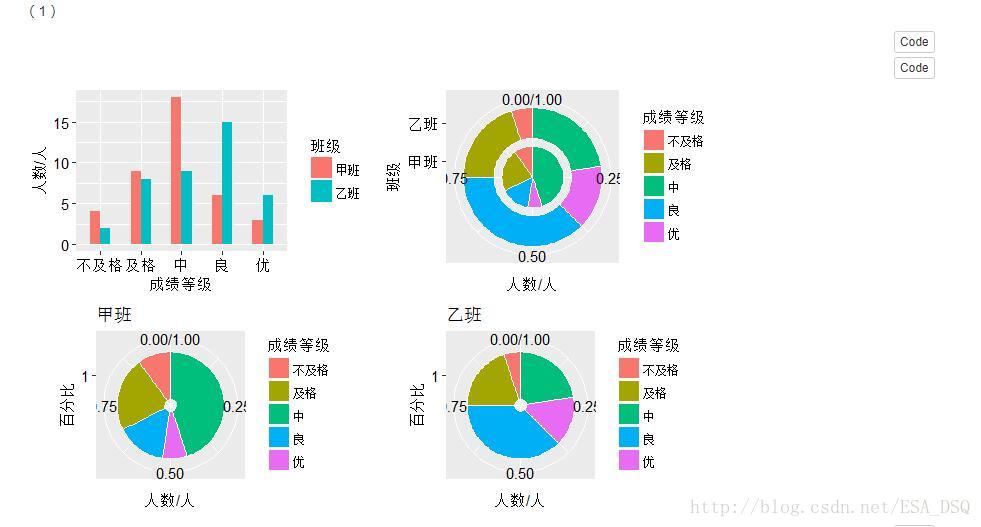
（1）根據上面的資料，畫出兩個班考試成績的複合柱形圖、環形圖和圖餅圖。
（2）比較兩個班考試成績分佈的特點。
（3）畫出雷達圖，比較兩個班考試成績的分佈是否相似。

3.隨機抽取25個網路使用者，得到他們的年齡資料（單位：週歲）見附錄。
（1）計算眾數、中位數。
（2）根據定義公式計算四分位數。
（3）計算平均數和標準差。
（4）計算偏態係數和峰態係數。
（5）對網民年齡的分佈特徵進行綜合分析。

4.某銀行為縮短顧客到銀行辦理業務等待的時間，準備採用兩種排隊方式進行試驗：一種是所有顧客都進入一個等待佇列；另一種是顧客在三個業務視窗處列隊三排等待。為比較哪種排隊方式使顧客等待的時間更短，兩種排隊方式各隨機抽取的9名顧客，得到第一中排隊方式的平均等待時間為7.2分鐘，標準差為，1.97分鐘，第二種排隊方式的等待時間（單位：min）見附錄。
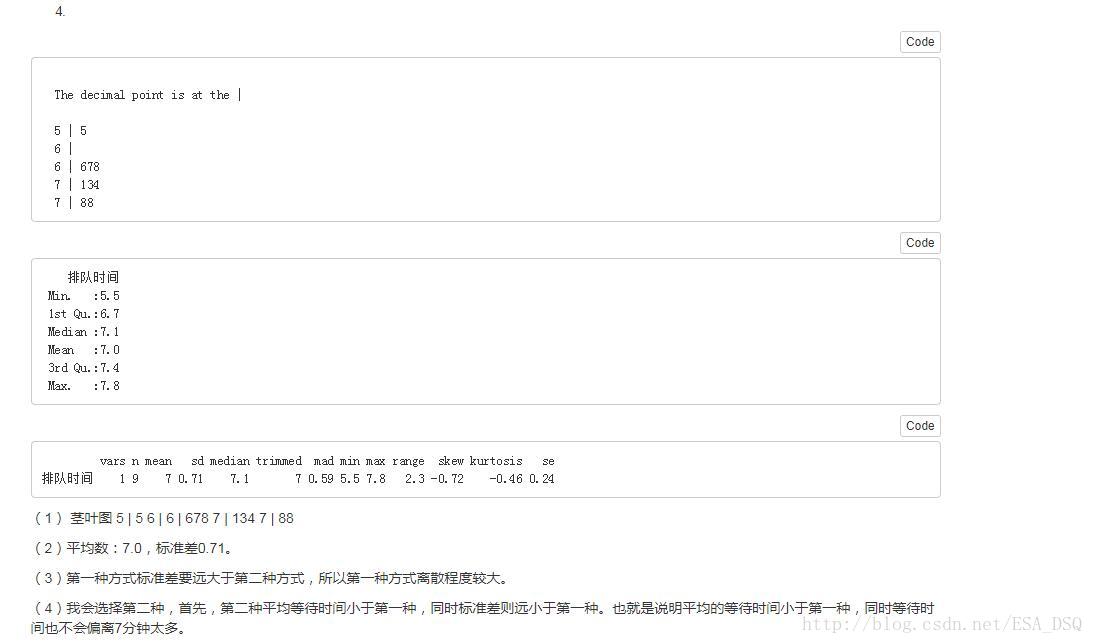
（１）畫出第二種排隊方式等待時間的莖葉圖。
（２）計算第二種排隊方式等待時間的平均數和標準差。
（３）比較兩種排隊方式等待時間的離散程度。
（４）如果讓你選擇一種排隊方式，你會選擇哪一種？試說明理由。

5.從均值為200、標準差為50的總體中，抽取n=100的簡單隨機樣本，用樣本均值`x估計總體均值。
a)描述重複抽樣的樣本均值的抽樣分佈。
b)不重複抽樣，總體單位數分別為10000、1000時的樣本均值的抽樣分佈。

2 引數估計與假設檢驗

1.某大學為了解學生每天上網的時間，在全校7500名學生中採取不重複抽樣方法隨機抽取36人，調查他們每天上網的時間（單位：小時） ，得到的資料見附錄。求該校大學生平均上網時間的置信區間，置信概率分別為90%、95%和99%。

2.假定兩個總體的標準差分別為：σ 1  =12，σ 2  =15，若要求誤差範圍不超過5，相應的置信水平為95%，假定n 1 =n 2

3.經驗表明，一個矩形的寬與長之比等於0.618的時候會給人們比較良好的感覺。某工藝品工廠生產的矩形工藝品框架的寬與長要求也按這一比例設計，假定其總體服從正態分佈，現隨機抽取了20個框架測得比值見附錄。在顯著性水平 ＝0.05時，能否認為該廠生產的工藝品框架寬與長的平均比例為0.618？。

4.一家大型超市連鎖店上個月接到許多消費者投訴某種品牌炸土豆片中60克一袋的那種土豆片的重量不符。店方猜想引起這些投訴的原因是運輸過程中沉積在食品袋底部的土豆片碎屑，但為了使顧客們對花錢買到的土豆片感到物有所值，店方仍然決定對來自於一家最大的供應商的下一批袋裝炸土豆片的平均重量（克）進行檢驗，假設陳述如下：
H 0 :μ≤60  H 1 :μ<60 
如果有證據可以拒絕原假設，店方就拒收這批炸土豆片並向供應商提出投訴。
（1）與這一假設檢驗問題相關聯的第一類錯誤是什麼？
（2）與這一假設檢驗問題相關聯的第二類錯誤是什麼？
（3）你認為連鎖店的顧客們會將哪類錯誤看得較為嚴重？而供應商會將哪類錯誤看得較為嚴重？

3 方差分析與迴歸分析

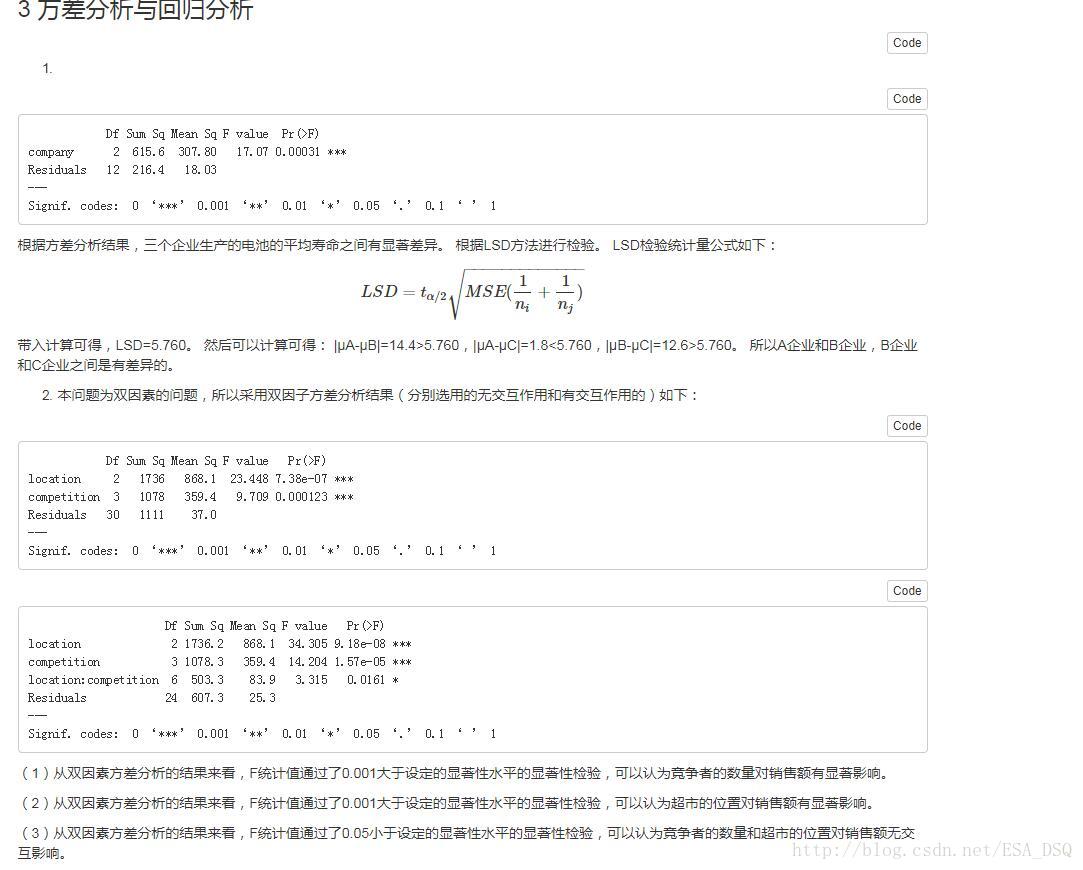
1.某家電製造公司準備購進一批5#電池，現有A、B、C三個電池生產企業願意供貨，為比較它們生產的電池質量，從每個企業各隨機抽取5只電池，經試驗得其壽命（單位：h）資料見附錄。試分析三個企業生產的電池的平均壽命之間有無顯著差異（α=0.05 ）。如果有差異，用LSD方法檢驗哪些企業之間有差異？

2.一家超市連鎖店的老闆進行一項研究，確定超市所在的位置和競爭者的數量對銷售額是否有顯著影響。獲得的月銷售額資料（單位：萬元）見附錄。取顯著性水平α=0.01 ，檢驗：
（1）競爭者的數量對銷售額是否有顯著影響。
（2）超市的位置對銷售額是否有顯著影響。
（3）競爭者的數量和超市的位置對銷售額是否有互動影響。

3.附錄中有隨機抽取的15家大型商場銷售的同類產品的有關資料（單位：元）。
（1）計算y與x 1   、y與x 2  之間的相關係數，是否有證據表明銷售價格與購進價格、銷售價格與銷售費用之間存線上性關係？
（2）根據上述結果，你認為用購進價格和銷售費用來預測銷售價格是否有用？
（3）用Excel進行迴歸，並檢驗模型的線性關係是否顯著（α=0.05 ）。
（4）解釋判定係數R 2  ，所得結論與問題（2）中是否一致?
（5）計算x 1  與x 2  之間的相關係數，所得結果意味著什麼？
（6）模型中是否存在多重共線性？你對模型有何建議？

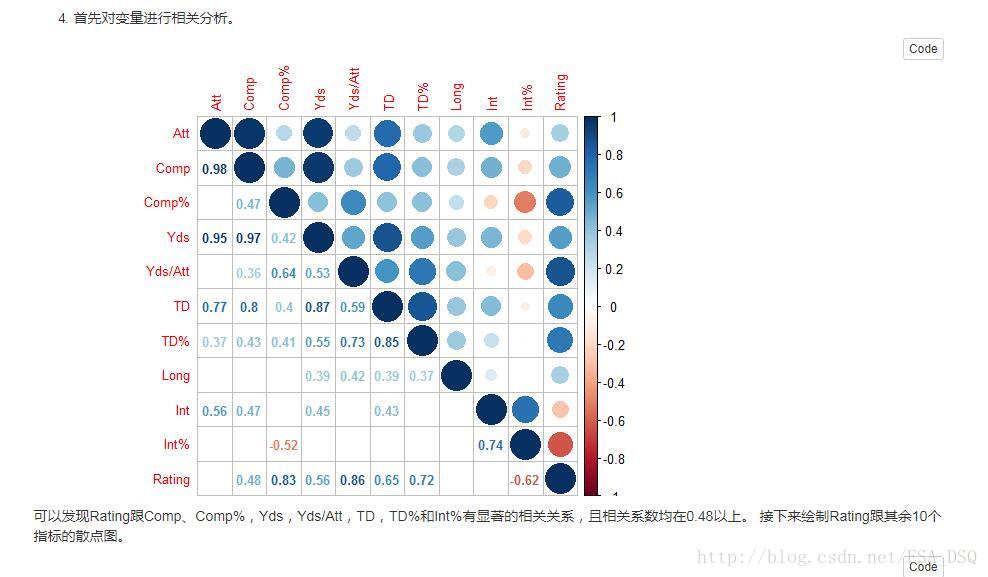
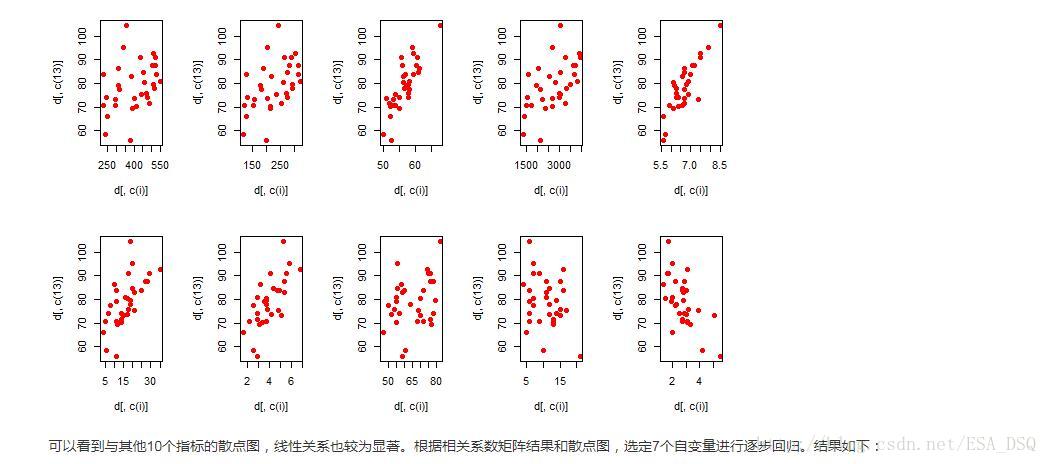
4.附錄中有32名美士足球運動員的rating及其他相關資訊。請建立一個迴歸模型以預測一位美士足球運動員的rating。提交報告包括：使用什麼方法建立的模型，該方法的執行結果，最終模型的解釋（擬合程度、預測誤差）。

這一份作業彙總從最原始的描述統計、引數估計、假設檢驗到基礎的方差分析與迴歸分析均有了。根據這裡的習題即可對前面的內容再次熟悉。
這裡就不多說了，我有一份比較完整的文件針對這份內容。這裡先給出節選部分的截圖。具體地址再給出。