強大數定律與弱大數定律的圖示詳解
程式碼來自:
https://stats.stackexchange.com/questions/2230/convergence-in-probability-vs-almost-sure-convergence?noredirect=1&lq=1
該連結中,
下面是強大數定律的R語言程式碼:
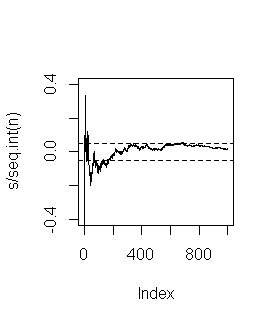
n <- 1000; m <- 50; e <- 0.05 s <- cumsum(1*(rbinom(n, size=1, prob=0.5) - 0)) plot(s/seq.int(n)-0.5, type = "l", ylim = c(-0.4, 0.4)) abline(h = c(-e,e), lty = 2) paste("---------------------")
Ctrl+a選中所有程式碼,然後Ctrl+Enter即可在Rstudio中運行了,
執行結果:
程式碼解釋:
rbinom(n,size,prob) n表示生成的隨機數數量,size表示進行貝努力試驗的次數,prob表示一次貝努力試驗成功的概率例
ylim指的是y軸的上下限設定
h(horizontal):表示水平橫線,程式碼中表示在水平畫兩條橫線,橫線對應的函式值分別是e和-e
lty:線條型別
---------------------------------------------------------------------------------------------
下面是弱大數定律的R語言程式碼:
n<-1000
m<-50
x <- matrix(1*(rbinom(n*m, size=1, prob=0.5) - 0.0), ncol = m)
print(x)
y <- apply(x, 2, function(z)(cumsum(z)/seq_along(z))-0.5)
matplot(y, type = "l", ylim = c(-0.4,0.4))
abline(h = c(-e,e), lty = 2, lwd = 2) 其中的u=0
其中cumsum(z)/seq_along(z)是整個函式體
做了m次實驗.每次實驗n個樣本.
針對向量a=(a1,...,an),
lwd是線條的寬度
apply(x,2,function(z)cumsum(z)/seq_along(z))表示矩陣中的每列值代入function(z)中
因為是服從伯努利分佈
執行結果如下:
apply的用法參考:
http://blog.fens.me/r-apply/
理論參考:
https://www.zhihu.com/question/21110761
https://en.wikipedia.org/wiki/Law_of_large_numbers#Weak_law
根據上面兩個連結的論述,弱大數定律在強大數定律之前被發現,
如果期望存在的話,弱大數定律與強大數定律同時成立,
如果期望不存在,那麼弱大數定律成立,強大數定律不成立。
也就是說,兩者的前提條件可以相同,也可以不相同。
上述兩個程式碼的情況是在兩者的前提條件都一致的情況下進行的圖形繪製。
所以兩段程式碼其實是同一個意思,只不過第二份程式碼畫了一大堆,所以能看到有跑出上下限制(-0.05,0.05)的,第一個程式碼只畫了一條線,所以很難碰到有跑出上下虛線的
相關推薦
強大數定律與弱大數定律的圖示詳解
程式碼來自:https://stats.stackexchange.com/questions/2230/convergence-in-probability-vs-almost-sure-convergence?noredirect=1&lq=1該連結中,下面是強大
大數定律與中心極限定律
1:為何能以某件事情發生的頻率作為該事件的概率的估計值? & 為何能以樣本均值作為總體期望的估計? →
強型別語言與弱型別語
簡單的說:強型別語言編譯質量更好,執行速度更快,但程式碼臃腫、死板。弱型別語言開發更敏捷,自由度更高,但效率略低。 強型別 比較嚴謹, 比較嚴格, 在保證資料的有效性來說, 會比較好一些, 也就比較穩定 但對初學者不大友善. 弱型別 易用, 上手快 但也經常出現一些問
諾威格定律與基因決定定律
IT 行業有許許多多有意思的規律。比如著名的摩爾定律和安迪-比爾定律,就是兩條從產業角度觀察得到的 IT 定律,而「70-20-10」定律,則是關於 IT 市場的一個規律。今天我們主要來介紹一下諾威格定律和基因決定定律,它們是從公司的角度,為公司的發展提出的規律
大數據入門第七天——MapReduce詳解
使用 sys distrib sent 作業 asi users tor war 一、概述 1.map-reduce是什麽 Hadoop MapReduce is a software framework for easily writing applica
大數據入門第七天——MapReduce詳解(下)
nbsp targe input pre 切片 入門 技術 log 過程 一、mapTask並行度的決定機制 1.概述 一個job的map階段並行度由客戶端在提交job時決定 而客戶端對map階段並行度的規劃的基本邏輯為: 將待處理數據執行邏輯
大數據入門第八天——MapReduce詳解(三)
大數 blog eve 分享圖片 shuf open src hid span 1/mr的combiner 2/mr的排序 3/mr的shuffle 4/mr與yarn 5/mr運行模式 6/mr實現join 7/mr全局圖
大數據hadoop入門之hadoop家族詳解
集成 查詢工具 人員 進一步 容錯 基礎知識 不同的 ima nbsp 大數據hadoop入門之hadoop家族詳解 大數據這個詞也許幾年前你聽著還會覺得陌生,但我相信你現在聽到hadoop這個詞的時候你應該都會覺得“熟悉”!越來越發現身邊從事hadoop開發或者是正在學習
【大數據分析】學習之路詳解
聯網 相同 規劃 mach 漏鬥圖分析 環境 分析方法 hbase reduce 以大數據分析師為目標,從數據分析基礎、JAVA語言入門和linux操作系統入門知識學起,系統介紹Hadoop、HDFS、MapReduce和Hbase等理論知識和hadoop的生態環境 一
php冒泡排序與快速排序實例詳解
lag ++ function 開始 ret light 記錄 php冒泡排序 php $a=array(‘3‘,‘8‘,‘1‘,‘4‘,‘11‘,‘7‘); print_r($a); $len = count($a); //從小到大 for($i=1;$i<$le
3dsmax2014的下載、安裝與註冊激活教程詳解
com cor 殺毒 系統 3dmax http 後退 tar 輸入 3dsmax2014的下載、安裝與註冊激活教程,雖然網上類似的教程文章不勝枚舉,但大多比較粗枝大葉,沒有詳細的步驟,尤其對於電腦小白來說,更是不易參考,今天我就教大家如何註冊破解3dsmax2014吧!
UML類圖與類的關系詳解--轉
position 好的 -a erp 生命 靜態 pan 雙向 單選 http://www.uml.org.cn/oobject/201104212.asp 原文地址 UML類圖與類的關系詳解 2011-04-21 來源:網絡
TCP協議的3次握手與4次揮手過程詳解
進行 發送數據 不存在 信息 隊列 協議 標識 方式 ar9 所謂三次握手(Three-Way Handshake)即建立TCP連接,就是指建立一個TCP連接時,需要客戶端和服務端總共發送3個包以確認連接的建立。所謂四次揮手(Four-Way Wavehand)即終止TCP
css-浮動與清除浮動的原理詳解(清除浮動的原理你知道嗎)
alt col ges mage all strong splay height http float元素A的特點: 脫離文檔流 靠向left或right float元素會和塊盒子重疊 準確來說,是塊盒子和A重疊,但塊盒子內容會浮動在A周圍 不會和inline元素重
UML類圖與類的關系詳解
enc pla 分享 包含關系 影響 基礎 rem 建模 基本組件 UML類圖與類的關系詳解 在畫類圖的時候,理清類和類之間的關系是重點。類的關系有泛化(Generalization)、實現(Realizati
Flask(十)flash與前臺交互post詳解
ace for pos pre 視圖 bmi temp 做的 輸入 Project name :Flask_Plan templates:templates static:static POST提交方式,首先要有表單 老實去改模板文件吧。 查詢窗口我準備放在頁面最頂上,就改
PHP與Java集成開發詳解(一)
new 編程語言 到你 其中 web-inf request 測試 add 輸入 很久以前,有人從www上看到看到天空上一個很亮的亮點,它就是Java語言,與此同時,在另一個地方一位夢想家也看到了一個亮點,它就是PHP。 時間一天天過去,這兩個亮點也變得越來越亮,很快,它
【轉】Quartz.net持久化與集群部署開發詳解
疑惑 sum 常用 drive wid res net github hub 轉自:http://www.cnblogs.com/knowledgesea/p/5145239.html 序言 我前邊有幾篇文章有介紹過quartz的基本使用語法與類庫。但是他的執行計劃都是被寫
seekg()/seekp()與tellg()/tellp()的用法詳解
文件操作 一個 需要 message ret 開頭 origin 部分 rom 本文轉載於:http://blog.csdn.net/mafuli007/article/details/7314917 (在tcp的文件發送部分有應用) 對輸入流操作:seekg()與tell
Storm筆記整理(五):可靠性分析、定時任務與Storm UI參數詳解
大數據 實時計算 Storm [TOC] 特別說明:前面的四篇Storm筆記中,關於計算總和的例子中的spout,使用了死循環的邏輯,實際上這樣做是不正確的,原因很簡單,Storm提供給我們的API中,nextTuple方法就是循環執行了,這相當於是做了雙層循環。因為後面在做可靠性acker案