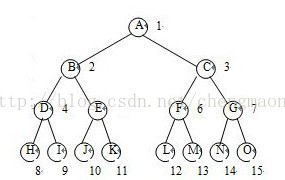
樹、二叉樹、滿二叉樹、完全二叉樹概念分清
自由樹
自由樹是一個連通的,無迴路的無向圖。
令G=(V,E)為一個無向圖。下面的表述是等價的。
1) G是自由樹。
2) G中任意兩個頂點由唯一一條簡單路徑得到。
3) G是連通的,但從E中去掉任何邊後得到的圖都是非連通的。
4) G是無迴路的,且|E|=|V|-1。
5) G是連通的,且|E|=|V|-1。
6) G是無迴路的,但新增任何邊到E中得到的圖包含迴路。
二叉樹
在電腦科學中,二叉樹是每個節點最多有兩個子樹的樹結構。通常子樹被稱作“左子樹”(left subtree)和“右子樹”(right subtree
二叉樹的每個結點至多隻有二棵子樹(不存在度大於2的結點),二叉樹的子樹有左右之分,次序不能顛倒。
二叉樹的第i層至多有2^(i-1)個結點;
深度為k的二叉樹至多有2^k-1個結點;(等比數列1+2+4+…+2^(k-1) = 2^k-1)。
對任何一棵二叉樹T,如果其終端結點數為n0,度為2的結點數為n2,則n0 = n2 + 1。
樹和二叉樹的三個主要差別:
1) 樹的結點個數至少為1,而二叉樹的結點個數可以為0;
2) 樹中結點的最大度數沒有限制,而二叉樹結點的最大度數為2;
3) 樹的結點無左、右之分,而二叉樹的結點有左、右之分。
滿二叉樹
一棵深度為k,且有2^k-1個節點的樹是滿二叉樹。
另一種定義:除了葉結點外每一個結點都有左右子葉且葉子結點都處在最底層的二叉樹。
這兩種定義是等價的。
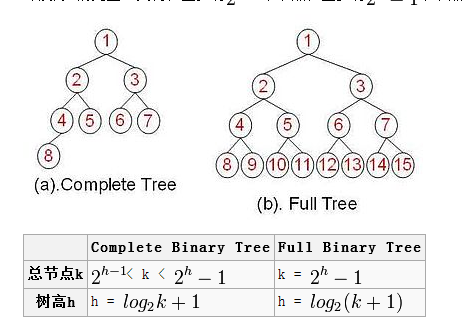
從樹的外形來看,滿二叉樹是嚴格三角形的,大家記住下面的圖,它就是滿二叉樹的標準形態:
所有內部節點都有兩個子節點,最底一層是葉子節點。
性質:
1) 如果一顆樹深度為h,最大層數為k,且深度與最大層數相同,即k=h;
2) 它的葉子數是: 2^(h-1)
3) 第k層的結點數是: 2^(k-1)
4) 總結點數是: 2^k-1 (2的k次方減一)
5) 總節點數一定是奇數。
6) 樹高:h=log2(n+1)。
完全二叉樹
完全二叉樹是由滿二叉樹而引出來的。對於深度為K的,有n個結點的二叉樹,當且僅當其每一個結點都與深度為K的滿二叉樹中編號從1至n的結點一一對應時稱之為完全二叉樹。
若設二叉樹的深度為h,除第 h 層外,其它各層 (1~h-1) 的結點數都達到最大個數,第h 層所有的結點都連續集中在最左邊,這就是完全二叉樹。
(大家好好理解一下上面兩個定義,是等價的~~)
滿二叉樹一定是完全二叉樹,完全二叉樹不一定是滿二叉樹。
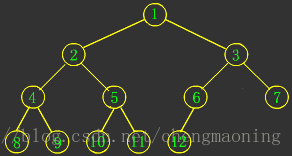
下面是完全二叉樹的基本形態:
完全二叉樹的性質:
1) 深度為k的完全二叉樹,至少有2^(k-1)個節點,至多有2^k-1個節點。
2) 樹高h=log2n + 1。
對滿二叉樹、完全二叉樹總結點及樹高的總結:
相關推薦
數據結構與算法(八)-二叉樹(斜二叉樹、滿二叉樹、完全二叉樹、線索二叉樹)
大型 結點 develop pac string col 限制 也會 斐波那契數 前言:前面了解了樹的概念和基本的存儲結構類型及樹的分類,而在樹中應用最廣泛的種類是二叉樹 一、簡介 在樹型結構中,如果每個父節點只有兩個子節點,那麽這樣的樹被稱為二叉樹(Binary
二叉樹基本概念(滿二叉樹、完全二叉樹,滿二叉樹,二叉樹的遍歷)
1. 二叉樹 二叉樹是每個節點最多有兩個子樹的樹結構。它有五種基本形態:二叉樹可以是空集;根可以有空的左子樹或右子樹;或者左、右子樹皆為空。 性質1:二叉樹第i層上的結點數目最多為 2{i-1} (i≥1)。性質2:深度為k的二叉樹至多有2{k}-1個結點(k≥1)
[樹] 6.49 判斷完全二叉樹、滿二叉樹 - C語言
題目來源:嚴蔚敏《資料結構》C語言版本習題冊 6.49 // 6.49 編寫演算法判別給定二叉樹是否為完全二叉樹 Status BiTreeIsComplete(BiTree T) { // 思路:完全二叉樹的層次遍歷應該是沒有NULL的 // 實現:把所有的結點都
完全二叉樹/ 滿二叉樹/二叉樹遍歷(前序、中序、後序、層序遍歷)
1.概念 在電腦科學中,二叉樹是每個節點最多有兩個子樹的樹結構。通常子樹被稱作“左子樹”(left subtree)和“右子樹”(right subtree)。二叉樹常被用於實現二叉查詢樹和二叉堆。二叉樹的每個結點至多隻有二棵子樹(不存在度大於2的結點),二叉樹的子
滿二叉樹、完全二叉樹、平衡二叉樹、哈夫曼樹
滿二叉樹:除了葉節點外每一個結點都有左右子女且葉節點都處在最底層的二叉樹。 這個滿二叉樹應該很好想象,就是一顆非常完美的樹,除了葉節點其他節點都有兩個孩子。 完全二叉樹:只有最下面的兩層結點度小於2,並且最下面一層的結點都集中在該層最左邊的若干位置的二叉樹。 也
滿二叉樹、完全二叉樹、完美二叉樹等概念的解釋
二叉樹:樹中每個節點至多有兩個子節點 二叉搜尋樹:對於樹中任何節點,如果其左子節點不為空,那麼該節點的value值永遠 >= 其左子節點;如果其右子節點不為空,那麼該節點的value值永遠 <= 其右子節點 滿二叉樹:樹中除了葉子節點,每個節點都
樹、二叉樹、滿二叉樹、完全二叉樹概念分清
自由樹 自由樹是一個連通的,無迴路的無向圖。 令G=(V,E)為一個無向圖。下面的表述是等價的。 1) G是自由樹。 2) G中任意兩個頂點由唯一一條簡單路徑得到。 3) G是連通的,但從E中去掉任何邊後得到的圖都是非連通的。 4)
資料結構----完全二叉樹和滿二叉樹以及前序、中序、後序遍歷
一) 滿二叉樹和完全二叉樹 1.滿二叉樹定義: 又叫Full Binary Tree. 除最後一層無任何子節點外,每一層上的所有結點都有兩個子結點(最後一層上的無子結點的結點為葉子結點)。也可以這樣理解,除葉子結點外的所有結點均有兩個子結點。節點數達到最大值
滿二叉樹、完全二叉樹、最優二叉樹(赫夫曼樹)、二叉排序樹、二叉判定樹
二叉排序樹(Binary Sort Tree)又稱二叉查詢樹。 它或者是一棵空樹;或者是具有下列性質的二叉樹: (1)若左子樹不空,則左子樹上所有結點的值均小於它的根結點的值; (2)若右子樹不空,則右子樹上所有結點的值均大於它的根結點的值; (3)左、右子樹也分別為二叉排序樹;
自己動手作圖深入理解二叉樹、滿二叉樹及完全二叉樹
[toc] #### 一、背景 二叉樹是資料結構中的重點,也是難點。二叉樹是一種非線性結構,比陣列、棧、佇列等線性結構相比複雜度更高,想要做到心中有“樹”,需要自己動手畫圖、觀察、思考,才能領會其真諦。該文將會結合圖形,深入理解二叉樹、滿二叉樹及完全二叉樹的概念。 #### 二、基本概念 ##### 2.1
1、如何判斷一棵樹是否是完全二叉樹?
出現 層序 null bool ron 進行 while 代碼 新的 思路:通過樹的層序遍歷進行判斷。結點入隊時,當出現一個結點的孩子結點為空時,則之後就不能有新的結點入隊。 若沒有,則是完全二叉樹,否則不是完全二叉樹。 層序遍歷代碼: int after = 1;/
二叉樹的非遞迴遍歷(先序、中序、後序和層序遍歷)
[前文] 二叉樹的非遞迴遍歷有 先序遍歷、中序遍歷 、後續遍歷 和 層序遍歷。 非遞迴演算法實現的基本思路:使用堆疊。而層序遍歷的實現:使用佇列。 如下圖所示的二叉樹: 前序遍歷順序為:ABCDE (先訪問根節點,然後先序遍歷其左子樹,最後先序遍歷
資料結構實驗-C語言-二叉樹的建立,前、中、後序遍歷的遞迴演算法和非遞迴演算法,求葉子結點數目,求二叉樹深度,判斷二叉樹是否相似,求二叉樹左右子樹互換,二叉樹層序遍歷的演算法,判斷二叉樹是否是完全二叉樹
1.實驗目的 熟練掌握二叉樹的二叉連結串列儲存結構的C語言實現。掌握二叉樹的基本操作-前序、中序、後序遍歷二叉樹的三種方法。瞭解非遞迴遍歷過程中“棧”的作用和狀態,而且能靈活運用遍歷演算法實現二叉樹的其它操作。 2.實驗內容 (1)二叉樹的二叉連結串列的建立 (2)二叉樹的前、中、後
二叉樹遍歷C++(前、中、後序遍歷,層次遍歷、深度遍歷)
一.使用c++進行前中後遍歷,層次和深度遍歷(非遞迴) 二.程式碼 #include<iostream> #include<queue> #include<vector> #include<stack> using name
222. 完全二叉樹的節點個數(中等、樹)
給出一個完全二叉樹,求出該樹的節點個數。 說明: 完全二叉樹的定義如下:在完全二叉樹中,除了最底層節點可能沒填滿外,其餘每層節點數都達到最大值,並且最下面一層的節點都集中在該層最左邊的若干位置。若最底層為第 h 層,則該層包含 1~ 2h 個節點。 示例:
JAVA 先序、中序、後序、層序,遞迴非遞迴遍歷二叉樹
定義一個二叉樹 package com.niuke.binaryTree; public class binaryTree { int data; binaryTree left; binaryTree right; public binaryTree(int
二叉樹(先、中、後、層次遍歷,判斷同構和是否為完全二叉樹)
二叉樹基本操作 二叉樹的結構定義 二叉樹的建立(遞迴) 訪問節點 先序遍歷 中序遍歷 後序遍歷 層次遍歷 判斷是否同構 判斷一顆二叉樹是否為完全二叉樹 二叉樹的結構定義
完美二叉樹、完全二叉樹、完滿二叉樹
1、二叉樹(Binary Tree) 1.1 什麼是二叉樹(Binary Tree) 每個結點至多擁有兩棵子樹(即二叉樹中不存在度大於2的結點),並且,二叉樹的子樹有左右之分,其次序不能任意顛倒。 1.2 二叉樹的性質 若二叉樹的層次從0開始,
二叉樹的先序建立,先序遍歷、中序遍歷、後序遍歷、全部結點數、二叉樹深度、葉子結點數、二叉樹左右子樹交換
#include<stdlib.h> #include<stdio.h> #include<conio.h> typedef char t; //定義資料型別 typedef
3 分鐘理解完全二叉樹、平衡二叉樹、二叉查詢樹
大傢伙,我是張拭心,今天給大家分享的是常見的三種二叉樹:完全二叉樹、平衡二叉樹、二