經典迴圈連結串列之約瑟夫問題：標號從1到n的n個人圍成一個圈，從1開始計數到m的人退出圈子，然後從退出的下一個人開始接著從1計數，數到m的人後繼續退出，最後只剩下一個人，求剩下人的編號。這便是約瑟夫問題的模型。

經典迴圈連結串列之魔術師發牌問題：魔術師手中有A、2、3……J、Q、K十三張黑桃撲克牌。在表演魔術前，魔術師已經將他們按照一定的順序疊放好（有花色的一面朝下）。魔術表演過程為：一開始，魔術師數1，然後把最上面的那張牌翻過來，是黑桃A；然後將其放到桌面上；第二次,魔術師數1、2；將第一張牌放到這些牌的最下面，將第二張牌翻轉過來，正好是黑桃2；第三次，魔術師數1、2、3；將第1、2張牌依次放到這些牌的最下面，將第三張牌翻過來正好是黑桃3；……直到將所有的牌都翻出來為止。問原來牌的順序是如何的。

連結串列相交：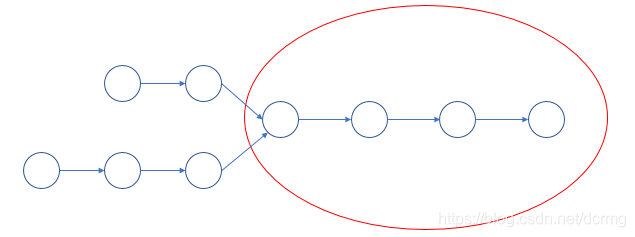

 

#include<stdio.h>
#include<stdlib.h>
#include<string.h>


//定義單向迴圈連結串列結點
typedef struct cNode{
    int data;
    struct cNode* next;
}cnode;

cnode* create_cNode(const int length){
    cnode* head = (cnode*)malloc(sizeof(cnode));
    cnode* p = head;
    for(int i=0;i<length;i++){
        p->next = (cnode*)malloc(sizeof(cnode));
        p->next->data = i+1;
        p=p->next;        
    }
    p->next = head->next;
    return head;
}

//列印所有結點
void print_cNode(cnode* cNode){
    cnode* p = cNode->next;
    while(p->next!=cNode->next){
        printf("%d\n",p->data);
        p=p->next;
    }    
    printf("%d\n",p->data);
}

//判斷一個連結串列是否帶環
//思路：設定一個快指標一次走2步，一個慢指標一次走1步，如果快指標與慢指標相遇則帶環
int with_loop_or_not(cnode* cNode){
    if(cNode==NULL){
        return 0;
    }
    cnode* fast = cNode->next;
    cnode* slow = cNode;
    while(fast!=slow && fast->next!=NULL&&fast->next->next!=NULL){
        fast = fast->next->next;
        slow = slow-next;
    }
    if(fast==slow){
        return 1;
    }
    else{
        return 0;
    }
}

//尋找帶環連結串列的入口
//思路： 對於帶環連結串列，從求出的相遇點挨個向下走，
//另一個指標從頭結點挨個向下走，兩個指標相遇的地方就是環入口

cnode* loop_enter(cnode* cNode){
    //先求出快慢指標在環內的相遇點
    if(cNode==NULL){
        return 0;
    }
    cnode* fast = cNode->next;
    cnode* slow = cNode;
    while(fast!=slow && fast->next!=NULL&&fast->next->next!=NULL){
        fast = fast->next->next;
        slow = slow-next;
    }
    //求入口
    cnode* step = head;
    cnode* loop_step = fast;
    while(step!=loop_step){
        step=step->next;
        loop_step=loop_step->next;
    }
    return step; //入口點
}

//判斷連結串列是否相交
//相交的意思是兩個連結串列的尾部若干個結點是重合的。
//方法一：分別求兩個連結串列的尾指標， 若兩個尾指標相等則相交。
//方法二：把其中一個連結串列的首尾相連，在此基礎上，若第二個連結串列存在環，則兩個連結串列相交

//約瑟夫問題
void ysf(cnode* cNode,int n, int m){
    cnode* p=cNode;    
    while(p->next!=p){
        int k = 1;
        if(k!=m){
            p=p->next;
            k+=1;
        }
        cnode* s = p->next;
        p->next = s->next;
        free(s);        
        }
    printf("%d\n",p->data);    
}

//魔術師發牌問題
cnode* mss(int length){
    cnode* head = (cnode*)malloc(sizeof(cnode));
    cnode* p = head;
    for(int i=0;i<length;i++){
        p->next = (cnode*)malloc(sizeof(cnode));
        p->next->data = 0;
        p=p->next;        
    }
    p->next = head->next;


    p = head->next;
    p->data = 1;
    for(int num = 2;num<=13;num++){
        int i = 0;
        while(i<num){
            p = p->next;
            if(p->data==0){
                i++;
            }
        }
        p->data = num;
    }
    return head;
}

void main(){
    //cnode* cNode = create_cNode(41);
    cnode* mms_ = mss(13);
    print_cNode(mms_);
    //ysf(cNode,41,3);
    return ;
}