PCA、LDA的參考學習、理解、混亂、清晰的過程
部分資料來自他人部落格,基礎上進行理解
LDA參考 http://blog.csdn.net/warmyellow/article/details/5454943
LDA演算法入門
一. LDA演算法概述:
線性判別式分析(Linear Discriminant Analysis, LDA),也叫做Fisher線性判別(Fisher Linear Discriminant ,FLD),是模式識別的經典演算法,它是在1996年由Belhumeur引入模式識別和人工智慧領域的。性鑑別分析的基本思想是將高維的模式樣本投影到最佳鑑別向量空間,以達到抽取分類資訊和壓縮特徵空間維數的效果,投影后保證模式樣本在新的子空間有最大的類間距離和最小的類內距離,即模式在該空間中有最佳的可分離性。因此,它是一種有效的特徵抽取方法。使用這種方法能夠使投影后模式樣本的類間散佈矩陣最大,並且同時類內散佈矩陣最小。就是說,它能夠保證投影后模式樣本在新的空間中有最小的類內距離和最大的類間距離,即模式在該空間中有最佳的可分離性。
二. LDA假設以及符號說明:
假設對於一個![]() 空間有m個樣本分別為x1,x2,……xm 即 每個x是一個n行的矩陣,其中
空間有m個樣本分別為x1,x2,……xm 即 每個x是一個n行的矩陣,其中![]() 表示屬於i類的樣本個數,假設有一個有c個類,則
表示屬於i類的樣本個數,假設有一個有c個類,則![]() 。
。
![]() ………………………………………………………………………… 類間離散度矩陣
………………………………………………………………………… 類間離散度矩陣
![]() ………………………………………………………………………… 類內離散度矩陣
………………………………………………………………………… 類內離散度矩陣
![]() ………………………………………………………………………… 屬於i類的樣本個數
………………………………………………………………………… 屬於i類的樣本個數
![]() …………………………………………………………………………… 第i個樣本
…………………………………………………………………………… 第i個樣本
![]() …………………………………………………………………………… 所有樣本的均值
…………………………………………………………………………… 所有樣本的均值
![]() …………………………………………………………………………… 類i
…………………………………………………………………………… 類i
三. 公式推導,演算法形式化描述
根據符號說明可得類i的樣本均值為:
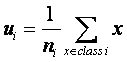 …………………………………………………………………… (1)
…………………………………………………………………… (1)
同理我們也可以得到總體樣本均值:
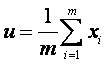 ………………………………………………………………………… (2)
………………………………………………………………………… (2)
根據類間離散度矩陣和類內離散度矩陣定義,可以得到如下式子:
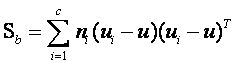 ……………………………………………… (3)
……………………………………………… (3)
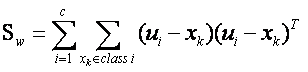 …………………………………… (4)
…………………………………… (4)
當然還有另一種類間類內的離散度矩陣表達方式:
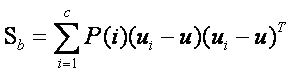
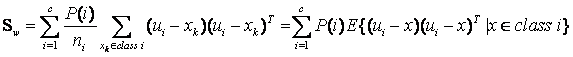 其中
其中![]() 是指i類樣本
是指i類樣本
的先驗概率,即樣本中屬於i類的概率(![]() ),把
),把![]() 代入第二組式子中,我們可以發現第一組式子只是比第二組式子都少乘了1/m,我們將在稍後進行討論,其實對於乘不乘該1/m
代入第二組式子中,我們可以發現第一組式子只是比第二組式子都少乘了1/m,我們將在稍後進行討論,其實對於乘不乘該1/m
我們可以知道矩陣![]() 的實際意義是一個協方差矩陣,這個矩陣所刻畫的是該類與樣本總體之間的關係,其中該矩陣對角線上的函式所代表的是該類相對樣本總體的方差(即分散度),(橫線是自己開始的認知混亂,把LDA公式當成了PCA快速計算裡面的一個步驟,造成錯誤理解)
的實際意義是一個協方差矩陣,這個矩陣所刻畫的是該類與樣本總體之間的關係,其中該矩陣對角線上的函式所代表的是該類相對樣本總體的方差(即分散度),(橫線是自己開始的認知混亂,把LDA公式當成了PCA快速計算裡面的一個步驟,造成錯誤理解)用各子類作為樣本,表示d個特徵向量之間的相關性(假設是d維空間,有d個特徵向量),那麼,非對角線上的元素所代表的是不同特徵向量之間的相關性,對角線元素反映的是d維中某個特徵向量內的各子類相關性,是該類樣本總體均值的協方差(即該類和總體樣本的相關聯度或稱冗餘度),所以根據公式(3)可知(3)式即把所有樣本中各個樣本根據自己所屬的類計算出樣本與總體的協方差矩陣的總和,這從巨集觀上描述了所有類和總體之間的離散冗餘程度。同理可以的得出(4)式中為分類內各個樣本和所屬類之間的協方差矩陣之和,它所刻畫的是從總體來看類內各個樣本與類之間(這裡所刻畫的類特性是由是類內各個樣本的平均值矩陣構成)離散度,其實從中可以看出不管是類內的樣本期望矩陣還是總體樣本期望矩陣,它們都只是充當一個媒介作用,不管是類內還是類間離散度矩陣都是從巨集觀上刻畫出類與類之間的樣本的離散度和類內樣本和樣本之間的離散度。
LDA做為一個分類的演算法,我們當然希望它所分的類之間耦合度低,類內的聚合度高,即類內離散度矩陣的中的數值要小,而類間離散度矩陣中的數值要大,這樣的分類的效果才好。
這裡我們引入Fisher鑑別準則表示式:
PCA參考 http://pinkyjie.com/2010/08/31/covariance/
思考總結:
一維向量, 均值:表示向量平均數 方差:向量取值離散度 標準差:向量取值距向量均值的距離,方差開根號
二維向量, 協方差:表示兩個向量之間的相關性,有2中計算方式
1、套用一維向量的方差公式,表示兩個向量之間的相關性 ,
cov(X,Y)=∑ni=1(Xi−X¯)(Yi−Y¯)n−1
或者直接通過相關性公式計算:cov(X,Y)指向量x與向量y的 相關性, 樣本矩陣MySample 10個樣本,每個樣本3個向量組成,所以這個樣本矩陣 是每一個樣本里麵包含了多個向量 ,cov(MySample),指的是MySample裡面的3個向量之間的相關性

協方差也只能處理二維問題,也就是隻能反映2個向量之間的相關性,那維數多了自然就需要計算多個協方差,就需要協方差矩陣了
因此上面的 三維向量的樣本矩陣MySample 向量x,y,z之間的相關性 通過如下協方差矩陣來表示,。

為了描述方便,我們先將三個維度的資料分別賦值:
| 123 | dim1 = MySample(:,1);dim2 = MySample(:,2);dim3 = MySample(:,3); |
計算dim1與dim2,dim1與dim3,dim2與dim3的協方差:
| 123 | sum( (dim1-mean(dim1)) .* (dim2-mean(dim2)) ) / ( size(MySample,1)-1 ) % 得到 74.5333sum( (dim1-mean(dim1)) .* (dim3-mean(dim3)) ) / ( size(MySample,1)-1 ) % 得到 -10.0889sum( (dim2-mean(dim2)) .* (dim3-mean(dim3)) ) / ( size(MySample,1)-1 ) % 得到 -106.4000 |
搞清楚了這個後面就容易多了,協方差矩陣的對角線就是各個維度上的方差,下面我們依次計算:
| 123 | std(dim1)^2 % 得到 108.3222std(dim2)^2 % 得到 260.6222std(dim3)^2 % 得到 94.1778 |
這樣,我們就得到了計算協方差矩陣所需要的所有資料。
直接呼叫Matlab自帶的cov函式進行驗證:
| 1 | cov(MySample) |

把我們計算的資料對號入座,是一摸一樣的
2、向量中心化,樣本矩陣轉置*矩陣,除以(n-1)
Update:今天突然發現,原來協方差矩陣還可以這樣計算,先讓樣本矩陣中心化,即每一維度減去該維度的均值,使每一維度上的均值為0,然後直接用新的到的樣本矩陣乘上它的轉置,然後除以(N-1)即可。其實這種方法也是由前面的公式通道而來,只不過理解起來不是很直觀,但在抽象的公式推導時還是很常用的!同樣給出Matlab程式碼實現:
| 12 | X = MySample - repmat(mean(MySample),10,1); % 中心化樣本矩陣,使各維度均值為0C = (X'*X)./(size(X,1)-1); |
注意區分:
1、矩陣轉置*矩陣【 (X'*X) 】 並不是等於 協方差矩陣, 而是協方差矩陣可以通過樣本矩陣轉置相乘,再除以(n-1)的方式快速計算得到。
向量*向量的轉置 = ?
2、LDA計算公式 既不是協方差的公式【差-積X*Y-和-均】,也不是 【矩陣轉置*矩陣(X'*X) 】
而是【差-積(向量與自己轉置的積(X*X'))- 和】
形式上更類似於 方差的概念【差-積(自己與自己)-和-均】 ,只不過方差裡面的自乘積元素是標量, LDA裡面自乘積的元素是向量
3、卷積 不要把卷積和相關性混了
matlab中,cov() 是相關係數計算函式 卷積函式 conv——一維卷積 conv2——二維卷積
矩陣沒有卷積,向量才有卷積
卷積:http://blog.csdn.net/anan1205/article/details/12313593
沒有矩陣卷積的,只有向量卷積。當然,如果你硬要把向量理解為一個1*n的矩陣,那也說的過去。 影象中是存在矩陣卷積操作的。
所謂兩個向量卷積,說白了就是多項式乘法。比如:p=[1 2 3],q=[1 1]是兩個向量,p和q的卷積如下:把p的元素作為一個多項式的係數,多項式按升冪(或降冪)排列,比如就按升冪吧,寫出對應的多項式:1+2x+3x^2;同樣的,把q的元素也作為多項式的係數按升冪排列,寫出對應的多項式:1+x。卷積就是“兩個多項式相乘取係數”。(1+2x+3x^2)×(1+x)=1+3x+5x^2+3x^3所以p和q卷積的結果就是[1
3 5 3]。記住,當確定是用升冪或是降冪排列後,下面也都要按這個方式排列,否則結果是不對的。你也可以用matlab試試p=[1 2 3]q=[1 1]conv(p,q)看看和計算的結果是否相同。
相關推薦
PCA、LDA的參考學習、理解、混亂、清晰的過程
部分資料來自他人部落格,基礎上進行理解 LDA參考 http://blog.csdn.net/warmyellow/article/details/5454943 LDA演算法入門 一. LDA演算法概述: 線性判別式分析(Linear Discriminant
四大機器學習降維演算法:PCA、LDA、LLE、Laplacian Eigenmaps
引言 機器學習領域中所謂的降維就是指採用某種對映方法,將原高維空間中的資料點對映到低維度的空間中。降維的本質是學習一個對映函式 f : x->y,其中x是原始資料點的表達,目前最多使用向量表達形式。 y是資料點對映後的低維向量表達,通常y的維度小於x的維度(當然提
企業、公網使用的路由協議 BGP / EBGP 學習使用理解及思路
根據 span 由器 com title inter process -o 鄰居 大型拓撲使用協議:BGP / EBGP今天剛學的配置,跟大家分享下。華為命令: bgp 64512 開啟BGP 運行AS號 64512 一臺機器運行一個AS號
python學習第五天:python基礎(字串、有序集合列表、元組;正確理解元組不可變)
首先,什麼是sequence(序列)操作? 字串的特性被稱為sequence(序列) H o w a r e y o u ? 就好像儲存在一個個連續的單元格里面,每個單
深入理解JVM學習筆記(二十六、JVM 記憶體分配----優先分配到eden&空間分配擔保)
一、優先分配到eden 我們寫一個程式來驗證物件優先分配到eden,原始碼如下: package com.zjt.test.jvm008; public class Main { public static void main(String[] args) { b
關於機器學習當中的正則化、範數的一些理解
The blog is fantastic! What I want to know is why we should regularlize and how we can regularlize, fortunately, this article tells all
深入理解JVM學習筆記(二十七、JVM 記憶體分配----大物件直接分配到老年代)
一、驗證 首先我們編寫如下程式 package com.zjt.test.jvm008; public class Main { public static void main(String[]
多執行緒學習一(執行緒、程序基本概念理解)
執行緒是程序中的實體,一個程序可以擁有多個執行緒,一個執行緒必須有一個父程序。執行緒不擁有系統資源,只有執行必須的一些資料結構;它與父程序的其它執行緒共享該程序所擁有的全部資源。執行緒可以建立和撤消執行緒,從而實現程式的併發執行。 執行緒也有就緒、阻塞和執行三種基本狀態。就
如何理解區分"人工智慧"、“機器學習”、“深度學習”三大巨星
都說教育要從娃娃抓起。學習新東西當然也要從基本概念抓起了,近兩年,人工智慧的真的是火遍大街小巷,不過,“人工智慧”也不是一人獨火,他還有兩個形影不離的隊友:“機器學習”與“深度學習”。這三個詞如同天團組合一般,出現在各種地方,有時甚至互為化身。那麼問題來了,人工
降維的四種方法:PCA、LDA、LLE、Laplacian Eigenmaps
知識點:降維的四種方法,PCA、LDA、LLE、Laplacian Eigenmaps 注意區分LDA: 資訊檢索中也有LDA(Latent Dirichlet allocation),主題模型,,表示文件的生成過程:先根據超參選擇主題,在根據主題的分佈取樣得到單詞,重
PCA、LDA、Kmeans、SVD/EVD、譜聚類之間的關係
PCA、LDA、Kmeans、SVD/EVD、譜聚類之間的關係 最近在研究譜聚類時,遷移到主成分分析(PCA),發現兩者有著驚人的相似之處,同時還牽扯到Kmeans、SVD,甚至LDA也有相通的地方(雖然LDA是有監督學習),因此在這裡寫一篇總結,描述一下以上各個模型之間的共通性,有助
學習Netty前對BIO、NIO、AIO的理解
概念 Netty是一個提供了易於使用的API的客戶端/伺服器框架 高併發NIO(非阻塞IO) 傳輸快,零拷貝(在Java中,記憶體分為堆疊常量池等。假設現在我們有一些資料,我們需要從IO裡面讀取並且放到堆裡面,那麼一般都會從IO流將資料讀入緩衝區,然後再從緩衝區裡
centos學習:理解環境變數 臨時、永久
臨時變數操作 name=dai echo $name name=$name"chen" //連線 echo $name #include <stdio.h> int main(i
特徵選擇和特徵提取區別 、PCA VS LDA
1.特徵提取 V.S 特徵選擇 特徵提取和特徵選擇是DimensionalityReduction(降維)的兩種方法,針對於the curse of dimensionality(維災難),都可以達到降維的目的。但是這兩個有所不同。 特徵提取(Feature
深入學習、理解select語句、delete語句以及其他SQL語句
1,delete from user as u where u.userid=6; 2,delete from user u where u.userid=6; 3,delete from user where userid=6; 4,delete u.* from user u where u.userid
深入理解JVM學習筆記(二十二、JVM 垃圾回收機制---如何回收垃圾---回收策略【複製演算法】)
上一節我們講到了標記-清除演算法因為需要進行兩次記憶體掃描導致效率不高,那麼這一節我們介紹一種複製演算法,比較好的解決了這個問題。 講複製演算法前,我們先回顧一下JVM的記憶體結構。JVM記憶體大體分為兩大塊,分別為執行緒共享區、執行緒獨佔區。
java學習中對泛型、Map、Collectiongs的一些理解
泛型: 1、泛型定義,一種安全機制。表明引數或者介面或者類的資料型別,般是 < > 表示 泛型,是在1.5之後才產生的,一般JDK“進化” 會更安全,更高效,更完整。 在1.5之前,沒有泛型都是用利用多型的思想強制轉化成某個型別再得到想要的值, 使用
我是這樣一步步理解--主題模型(Topic Model)、LDA(案例程式碼)
1. LDA模型是什麼 LDA可以分為以下5個步驟: 一個函式:gamma函式。 四個分佈:二項分佈、多項分佈、beta分佈、Dirichlet分佈。 一個概念和一個理念:共軛先驗和貝葉斯框架。 兩個模型:pLSA、LDA。 一個取樣:Gibbs取樣 關於LDA有兩種含義,一種是線性判別分析(Linear
Java 中級 學習筆記 1 JVM的理解以及新生代GC處理流程和常量池、執行時常量池、字串常量池的理解
寫在最前 從畢業到現在已經過去了差不多一年的時間,工作還算順利,但總是離不開CRUD ,我覺得這樣下去肯定是不行的,溫水煮青蛙,勢必有一天,會昏昏沉沉的迷失在溫水裡。所以,需要將之前學習JAVA 當中一些中高階部分的知識需要進行學習和記錄,並將其整理部落格,一起成長,一起努力。 JVM JAVA虛擬機器在執行
構建之法第八、九章學習
周期 常用 bcd 快速 區別 利益相關者 自省 生命 獲取 第八章:需求分析 這一章主要講述了軟件需求的類型、利益相關者、獲取用戶需求的常用方法和步驟、競爭性需求分析的框架NABCD、四象限方法、項目計劃和估計的技術。 確認軟件需求有以下步驟:1.獲取和引導需求、2.分析
