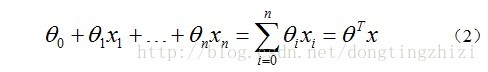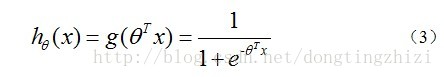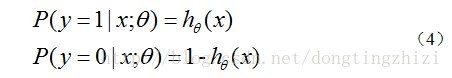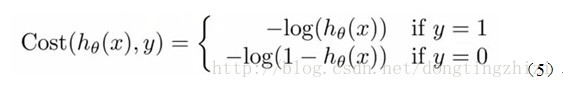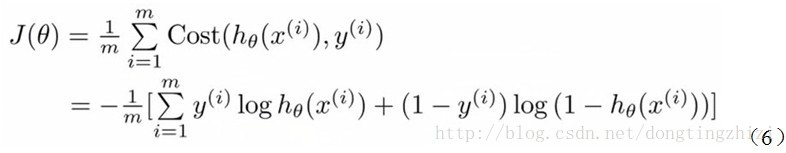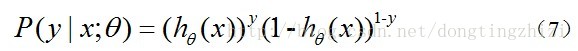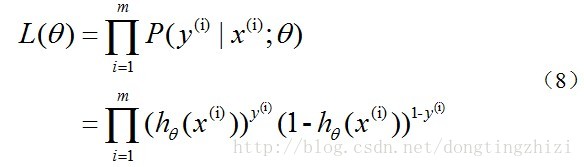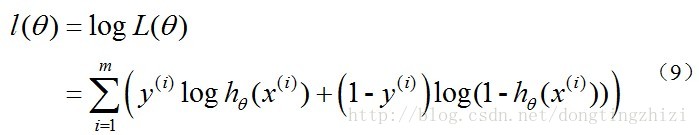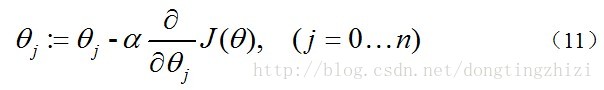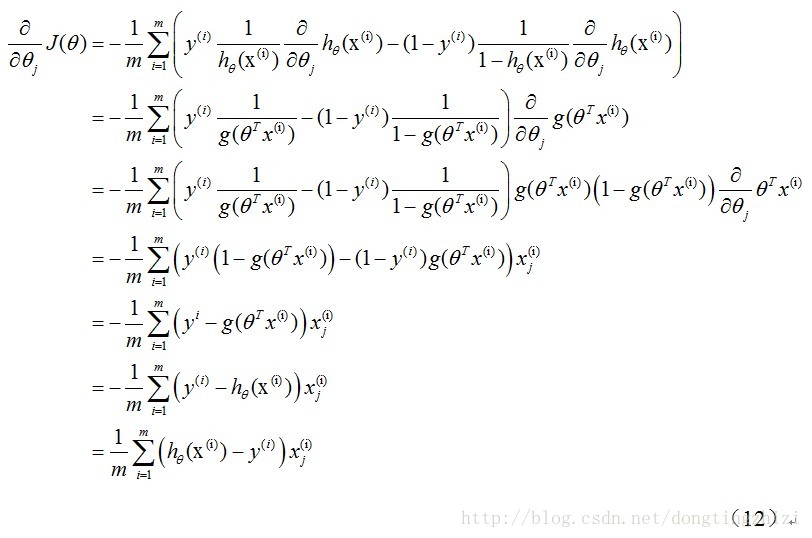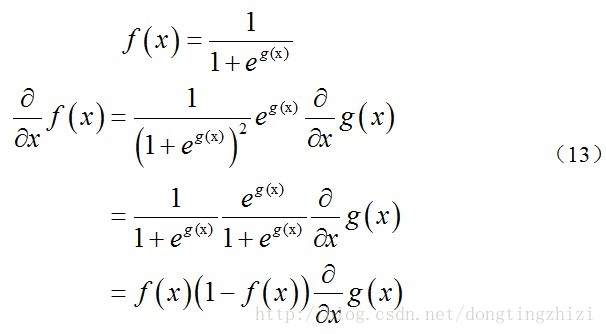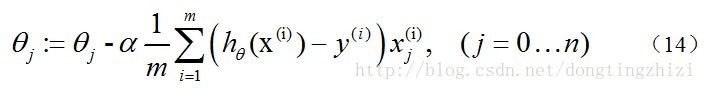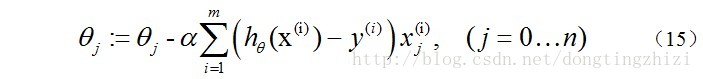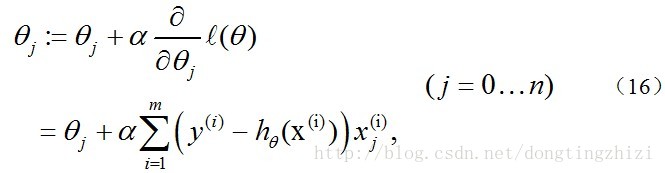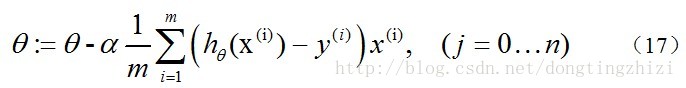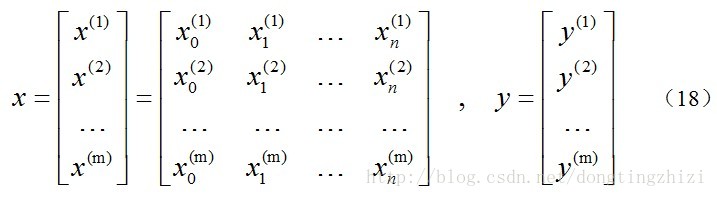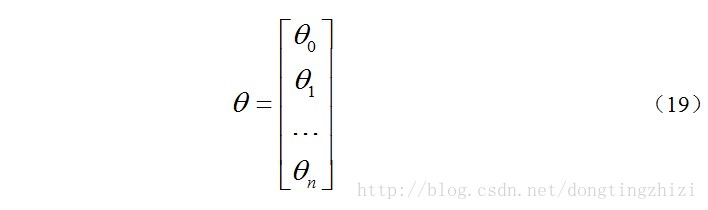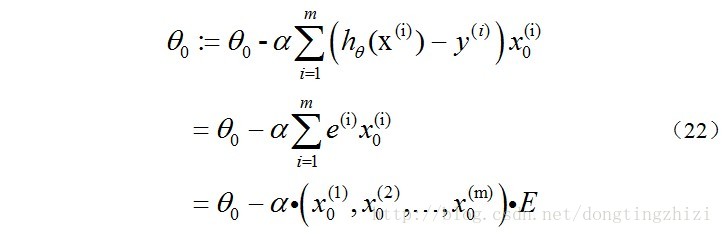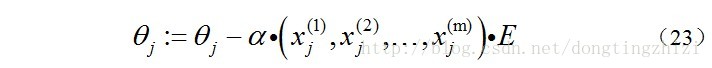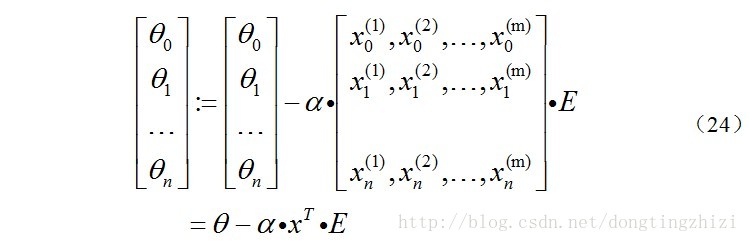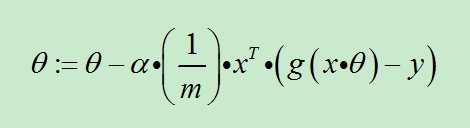Logistic迴歸總結

作者：洞庭之子

（2013年11月）

1.引言

看了Stanford的Andrew Ng老師的機器學習公開課中關於Logistic Regression的講解，然後又看了《機器學習實戰》中的LogisticRegression部分，寫下此篇學習筆記總結一下。

首先說一下我的感受，《機器學習實戰》一書在介紹原理的同時將全部的演算法用原始碼實現，非常具有操作性，可以加深對演算法的理解，但是美中不足的是在原理上介紹的比較粗略，很多細節沒有具體介紹。所以，對於沒有基礎的朋友（包括我）某些地方可能看的一頭霧水，需要查閱相關資料進行了解。所以說，該書還是比較適合有基礎的朋友。

本文主要介紹以下三個方面的內容：

（1）Logistic Regression的基本原理，分佈在第二章中；

（2）Logistic Regression的具體過程，包括：選取預測函式，求解Cost函式和J(θ)，梯度下降法求J(θ)的最小值，以及遞迴下降過程的向量化（vectorization），分佈在第三章中；

（3）對《機器學習實戰》中給出的實現程式碼進行了分析，對閱讀該書LogisticRegression部分遇到的疑惑進行了解釋。沒有基礎的朋友在閱讀該書的Logistic Regression部分時可能會覺得一頭霧水，書中給出的程式碼很簡單，但是怎麼也跟書中介紹的理論聯絡不起來。也會有很多的疑問，比如：一般都是用梯度下降法求損失函式的最小值，為何這裡用梯度上升法呢？書中說用梯度上升發，為何程式碼實現時沒見到求梯度的程式碼呢？這些問題在第三章和第四章中都會得到解答。

文中參考或引用內容的出處列在最後的“參考文獻”中。文中所闡述的內容僅僅是我個人的理解，如有錯誤或疏漏，歡迎大家批評指正。下面進入正題。

2. 基本原理

Logistic Regression和Linear Regression的原理是相似的，按照我自己的理解，可以簡單的描述為這樣的過程：

（1）找一個合適的預測函式（Andrew Ng的公開課中稱為hypothesis），一般表示為h函式，該函式就是我們需要找的分類函式，它用來預測輸入資料的判斷結果。這個過程時非常關鍵的，需要對資料有一定的瞭解或分析，知道或者猜測預測函式的“大概”形式，比如是線性函式還是非線性函式。

（2）構造一個Cost函式（損失函式），該函式表示預測的輸出（h

（3）顯然，J(θ)函式的值越小表示預測函式越準確（即h函式越準確），所以這一步需要做的是找到J(θ)函式的最小值。找函式的最小值有不同的方法，Logistic Regression實現時有的是梯度下降法（Gradient Descent）。

3. 具體過程

3.1  構造預測函式

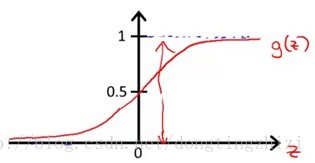
Logistic Regression雖然名字裡帶“迴歸”，但是它實際上是一種分類方法，用於兩分類問題（即輸出只有兩種）。根據第二章中的步驟，需要先找到一個預測函式（h），顯然，該函式的輸出必須是兩個值（分別代表兩個類別），所以利用了Logistic函式（或稱為Sigmoid函式），函式形式為：

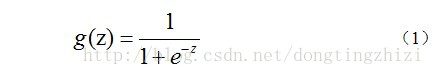
對應的函式影象是一個取值在0和1之間的S型曲線（圖1）。

圖1

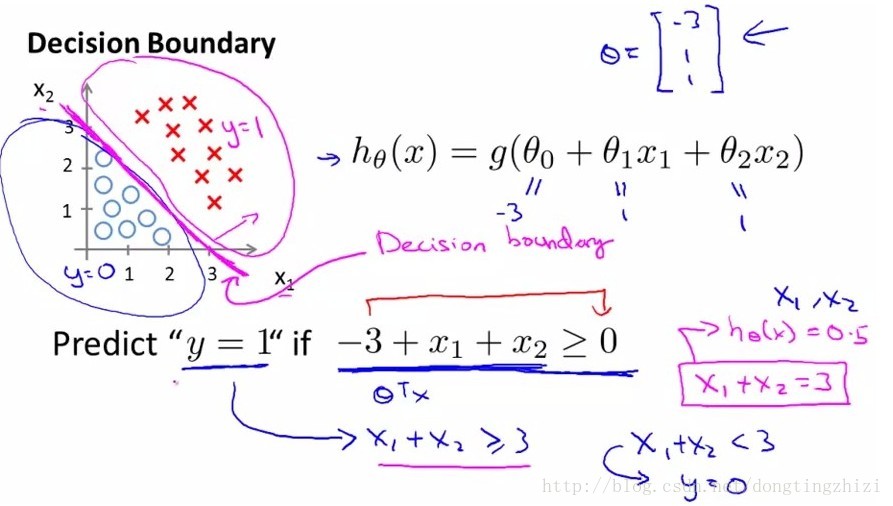
接下來需要確定資料劃分的邊界型別，對於圖2和圖3中的兩種資料分佈，顯然圖2需要一個線性的邊界，而圖3需要一個非線性的邊界。接下來我們只討論線性邊界的情況。

圖2

圖3

對於線性邊界的情況，邊界形式如下：

構造預測函式為：

hθ(x)函式的值有特殊的含義，它表示結果取1的概率，因此對於輸入x分類結果為類別1和類別0的概率分別為：

3.2  構造Cost函式

Andrew Ng在課程中直接給出了Cost函式及J(θ)函式如式（5）和（6），但是並沒有給出具體的解釋，只是說明了這個函式來衡量h函式預測的好壞是合理的。

實際上這裡的Cost函式和J(θ)函式是基於最大似然估計推導得到的。下面詳細說明推導的過程。（4）式綜合起來可以寫成：

取似然函式為：

對數似然函式為：

最大似然估計就是要求得使l(θ)取最大值時的θ，其實這裡可以使用梯度上升法求解，求得的θ就是要求的最佳引數。但是，在Andrew Ng的課程中將J(θ)取為（6）式，即：

因為乘了一個負的係數-1/m，所以J(θ)取最小值時的θ為要求的最佳引數。

3.3  梯度下降法求J(θ)的最小值

求J(θ)的最小值可以使用梯度下降法，根據梯度下降法可得θ的更新過程：

式中為α學習步長，下面來求偏導：

上式求解過程中用到如下的公式：

因此，（11）式的更新過程可以寫成：

因為式中α本來為一常量，所以1/m一般將省略，所以最終的θ更新過程為：

另外，補充一下，3.2節中提到求得l(θ)取最大值時的θ也是一樣的，用梯度上升法求（9）式的最大值，可得：

觀察上式發現跟（14）是一樣的，所以，採用梯度上升發和梯度下降法是完全一樣的，這也是《機器學習實戰》中採用梯度上升法的原因。

3.4  梯度下降過程向量化

關於θ更新過程的vectorization，Andrew Ng的課程中只是一帶而過，沒有具體的講解。

《機器學習實戰》連Cost函式及求梯度等都沒有說明，所以更不可能說明vectorization了。但是，其中給出的實現程式碼確是實現了vectorization的，圖4所示程式碼的32行中weights（也就是θ）的更新只用了一行程式碼，直接通過矩陣或者向量計算更新，沒有用for迴圈，說明確實實現了vectorization，具體程式碼下一章分析。

文獻[3]中也提到了vectorization，但是也是比較粗略，很簡單的給出vectorization的結果為：

且不論該更新公式正確與否，這裡的Σ(...)是一個求和的過程，顯然需要一個for語句迴圈m次，所以根本沒有完全的實現vectorization，不像《機器學習實戰》的程式碼中一條語句就可以完成θ的更新。

下面說明一下我理解《機器學習實戰》中程式碼實現的vectorization過程。

約定訓練資料的矩陣形式如下，x的每一行為一條訓練樣本，而每一列為不同的特稱取值：

約定待求的引數θ的矩陣形式為：

先求x.θ並記為A：

求hθ(x)-y並記為E：

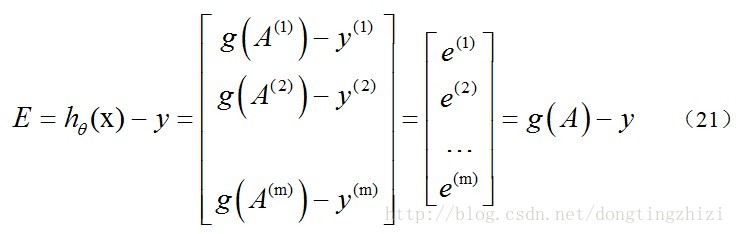
g(A)的引數A為一列向量，所以實現g函式時要支援列向量作為引數，並返回列向量。由上式可知hθ(x)-y可以由g(A)-y一次計算求得。

再來看一下（15）式的θ更新過程，當j=0時：

同樣的可以寫出θj，

綜合起來就是：

綜上所述，vectorization後θ更新的步驟如下：

（1）求A=x.θ；

（2）求E=g(A)-y；

（3）求θ:=θ-α.x'.E,x'表示矩陣x的轉置。

也可以綜合起來寫成：

前面已經提到過：1/m是可以省略的。

4. 程式碼分析

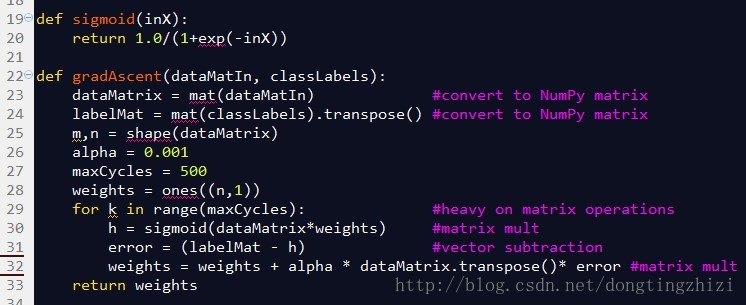
圖4中是《機器學習實戰》中給出的部分實現程式碼。

圖4

sigmoid函式就是前文中的g(z)函式，引數inX可以是向量，因為程式中使用了Python的numpy。

gradAscent函式是梯度上升的實現函式，引數dataMatin和classLabels為訓練資料，23和24行對訓練資料做了處理，轉換成numpy的矩陣型別，同時將橫向量的classlabels轉換成列向量labelMat，此時的dataMatrix和labelMat就是（18）式中的x和y。alpha為學習步長，maxCycles為迭代次數。weights為n維（等於x的列數）列向量，就是（19）式中的θ。

29行的for迴圈將更新θ的過程迭代maxCycles次，每迴圈一次更新一次。對比3.4節最後總結的向量化的θ更新步驟，30行相當於求了A=x.θ和g(A)，31行相當於求了E=g(A)-y，32行相當於求θ:=θ-α.x'.E。所以這三行程式碼實際上與向量化的θ更新步驟是完全一致的。

總結一下，從上面程式碼分析可以看出，雖然只有十多行的程式碼，但是裡面卻隱含了太多的細節，如果沒有相關基礎確實是非常難以理解的。相信完整的閱讀了本文，就應該沒有問題了！^_^。

【參考文獻】