【參考資料】 【1】《統計學習方法》 【2】《凸優化》 【3】小象學院 《凸優化》

凸集

直線和線段的表達

設$x_1 \ne x_2$是$R^n$空間上的兩個點，具有存在下列定義的點： $y = \theta x_1 + (1 - \theta)x_2$組成一條過兩點的直線，當$\theta$取值在0、1之間表示一個線段。

另外一種表述方式:$y = x_2 + (x_2 - x_1)\theta$即$x_2$作為一個基點，直線表示為基點加上兩點距離乘以一個引數形成偏移的點的集合。

仿射集合

仿射定義: 對於$x_1, x_2 \in C \quad \theta \in R$存在$\theta x_1 + \theta(1-x_2) \in C$ 理解：這個集合對於線性變換具備封閉性

凸集

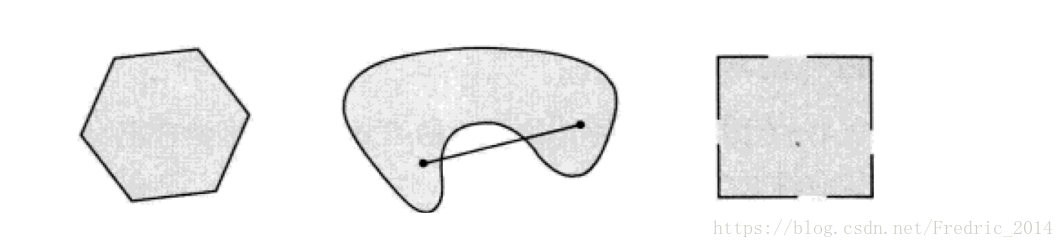
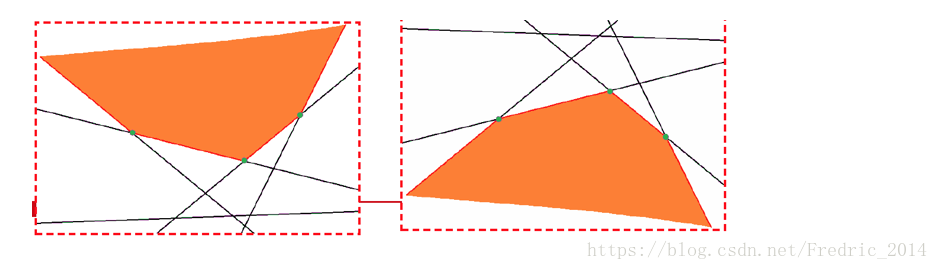
凸集定義：對於$x_1, x_2 \in C \quad \theta \in [0,1]$存在$\theta x_1 + \theta(1-x_2) \in C$ 從簡單幾何圖形上理解，即如下例

支撐超平面

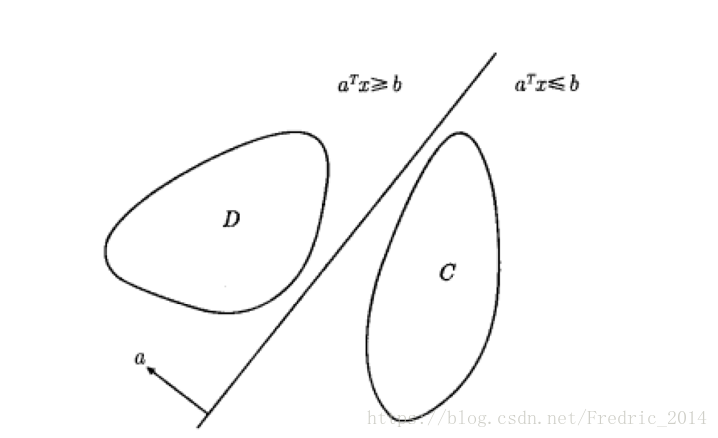
超平面分離定理

超平面$\{ x | a^Tx = b\}$分離了兩個不相交的凸集C和D，其中也稱$a^Tx \ge b \quad a^Tx \le b$為超平面劃分出來的兩個半空間。

備註：當待分割的兩個集合不是凸集，則未必存在一個超平面能夠分割兩個集合，那麼這個時候如果取一個超平面能夠是分割後損失最小（即儘可能的分割清楚），就是類似SVM這樣的演算法要完成的事情。

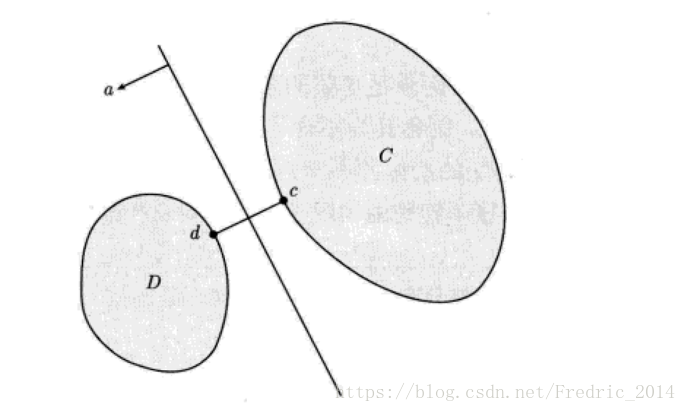
通過做垂直於兩個凸集最短距離的超平面來作一個分割超平面，如下：

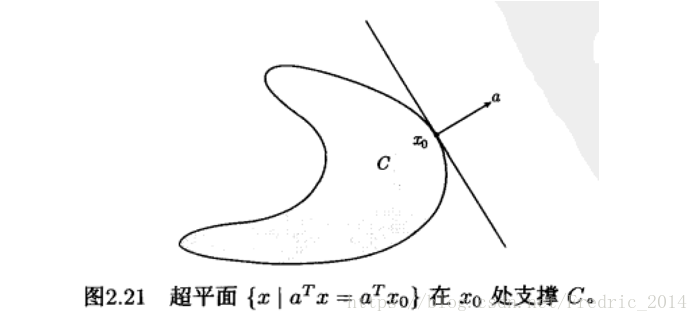
支撐超平面

定義：$a \ne 0$ 對於任何$x \in C$

凸函式

凸函式定義

定義函式f:$R^n \to R$是凸的，如果domf（定義域）是凸集，且對於任意$x \quad y \in domf \quad 0 \le \theta \le 1$有：

$f(\theta x + (1 - \theta y)) \le \theta f(x) + (1 - \theta)f(x)$

保凸運算

1. 非負加權求和

嚴格的凸（凹）函式的非負加權求和也是凸（凹）函式 $ f = w_1f_1 + w_2f_2 + … + w_nf_n$

2. 複合仿射對映

$g(x) = f(Ax + b)$

若函式f是凸（凹）函式，則g也是凸（凹）函式

3. 逐點最大或逐點上確界

若$f_1 \quad f_2$是凸函式，則$f = max(f_1, f_2)$仍然是凸函式

同時N條直線（凸函式）逐點求下确界是凹函式（必然有一個最大值，用在拉格朗日對偶中），如下圖：

拉格朗日對偶

凸優化問題定義:

假設$f(x) \quad c_i(x) \quad h_j(x)$是定義在$R^n$空間上的連續可微函式，考慮約束最優化問題:

求解：$min_{x \in R^n}f(x)$ 存在約束條件: $c_i(x) \le 0, i=1,2...k$ $h_j(x)=0, j = 1,2...l$

引入拉格朗日函式:

$L(x, \alpha, \beta)=f(x) + \sum_{i=1}^k\lambda_ic_i(x) + \sum_{j=1}^l\beta_jh_j(x)$ 其中$ \alpha_i \quad \beta_j$是拉格朗日乘子。

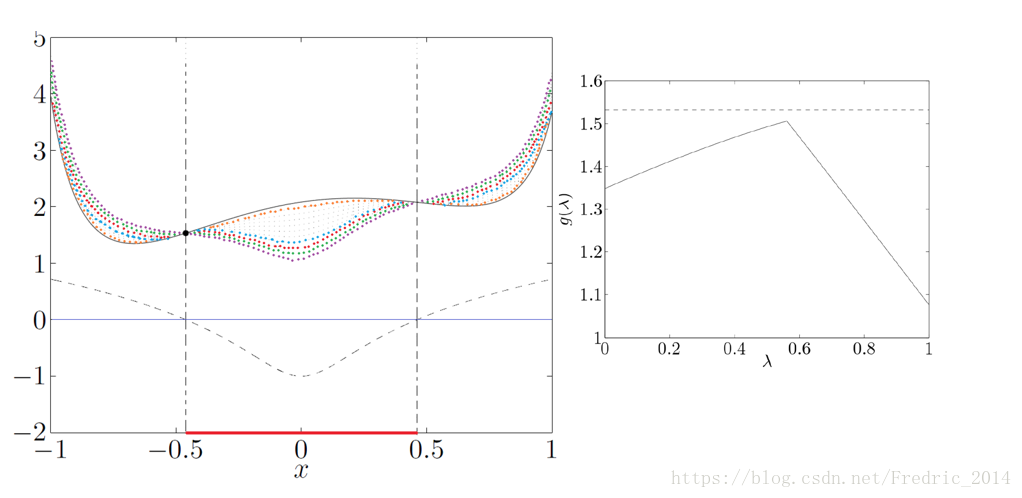
當我們固定x時，只考慮$\lambda$，則拉格朗日函式可以看作是$\lambda$作為直線的函式集，那麼這些函式集的下确界構成一個凹函式，必然有極大值。

上圖的備註：

1. 上圖針對最優化問題所構造的拉格朗日函式$L(x,lambda)=f(x)+\lambda h(x)$
2. 左圖x軸紅線部分代表x的取值範圍，即最優化問題的約束
3. 黑色實現代表原始函式f(x)
4. 不同顏色的虛線，代表不同$\lambda$下的$g(\lambda)=f(x)+\lambda h(x)$
5. 左圖對$min \quad g(\lambda)$左圖
6. 可以得到結論，當我們對左圖$min \quad g(\lambda)$求最大值，也就得到了原始問題f(x)的最小值（重要）

拉格朗日對偶性:

這部分用於理解為什麼拉格朗日對偶函式的最大值，能夠對應到原始函式的最小值。

重新來看拉格朗日函式的定義

$L(x, \alpha, \beta)=f(x) + \sum_{i=1}^k\lambda_ic_i(x) + \sum_{j=1}^l\beta_jh_j(x)$

由於$c_i(x)$是恆小於0的，因此整個$\sum_{i=1}^k\lambda_ic_i(x) + \sum_{j=1}^l\beta_jh_j(x)$的最大值是0。也就是說當$\sum_{i=1}^k\lambda_ic_i(x) + \sum_{j=1}^l\beta_jh_j(x)$