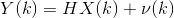卡爾曼(Kalman)濾波(一)--Kalman濾波的本質
1.Kalman濾波的簡介
接觸過訊號處理的朋友應該清楚,訊號在傳輸過程中必然受到噪聲干擾(外界的二和內部的),使得輸出訊號具有隨機性,為了最大限度降低這種干擾,就需要從混雜在一起的各種訊號中提取自己想要的訊號,這過程稱之為濾波,濾波的方法因訊號而異。
對於確定性訊號,由於其具有確定的頻譜,因此可以設定滿足相應頻率特性的filter,比如LPF,HPF,BPF等,抑制干擾訊號的通過,這一類的filter既可用模擬(Analog)的filter實現,也可以用數字(Digital)的實現,通常被稱為常規濾波。
對於隨機訊號,由於其具與確定的功率譜,因此可以根據有用訊號和干擾訊號的功率譜來設計對應的filter,比如維納濾波(Winer),它就是基於功率譜的分解從而設計得來的,基本機理同常規濾波相似,但由於其基於頻域,並且還要求解維納-霍普夫方程,計算量和儲存量都很大,所以很少被應用,因此很多年後一個叫Kalman的人提出了一種思想,通過那些與有用訊號相關的觀測量中估計出有用訊號,這一思路就是後來著名的Kalman濾波演算法,這個演算法真的用處大大啊。
Kalman引入了狀態空間的概念,並用狀態方程來描述輸入輸出,在估計過程中使用狀態方程、觀測方程,以及系統噪聲和觀測噪聲的激勵構成完整的濾波演算法。另外,與維納濾波不同的是,該濾波演算法是基於時域的,優美的避免了維納濾波在頻域上的限制,不僅可以估計平穩訊號,而且可以估計非平穩訊號以及多維,因而廣泛被應用。
2.估計問題
2.1估計問題的簡介
熟悉Kalman的朋友會了解,Kalman濾波本質上來說其實就是一種實時遞推演算法,以隨機訊號作為處理物件,輸入為系統的觀測量,輸出為系統的狀態和引數的估計值,而輸入和輸出之間又是通過兩種更新演算法(時間更新和觀測更新)聯絡在一起的,估計值是通過狀態方程和觀測方程估計而來,因此這樣一看,我們所說的Kalman濾波其實是有別於上面說的常規濾波的,說白了,Kalman濾波演算法就是一種最優估計問題。
我們把通過對觀測資料進行處理而得到所需引數的估計值的這一過程稱作估計問題,估計問題通常分兩類:1)引數估計:系統的結構引數部分或全部未知;2)狀態估計:在需要知道系統狀態時,由於某些具體限制導致系統部分或全部狀態未知。一般的,一個典型的估計問題由三部分組成:1)先驗知識;2)約束條件;3)估計準則函式;其中準則函式明顯是用來衡量一個估計的好壞的。
2.2估計方法與準則函式
在實際應用中,我們總希望得到的估計值越接近實際值越好,即最優估計,但是呢,實際情況下卻不那麼容易達到,為什麼呢,因為準則函式的選取各不相同啊,導致最優估計並不唯一,只有選擇的準則函式適合了,才可能得到想要的最優估計。通常,準則函式又叫做損失函式,這一損失函式是根據先驗知識確定的,然後使其最小化或最大化,損失函式不同,導致估計方法也不同,根據前人學者們的寶貴經驗,實踐中比較可行的準則函式有:直接誤差準則、誤差函式矩準則、直接概率準則,估計方法與估計準則密切聯絡,常用的估計方法有:最小二乘估計(LS)或最小平方誤差估計(MSE)、最小方差估計、極大似然估計、極大後驗估計、核估計。
2.3估計模型
通常考慮下面離散模型:
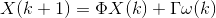
其中,X(k)是系統的n維狀態向量;Y(k)是系統的m維觀測向量;w(k)是系統的p維隨機干擾向量;v(k)是系統的r維觀測噪聲向量;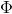
參考:https://zh.wikipedia.org/wiki/%E5%8D%A1%E5%B0%94%E6%9B%BC%E6%BB%A4%E6%B3%A2
相關推薦
cv2使用卡爾曼濾波(Kalman Filter)捕捉滑鼠運動
本文主要介紹在cv2中使用Kalman濾波捕捉滑鼠運動。 cv2.KalmanFilter(dynamParams=None,#狀態的維度 measureParams=None, #測量的維度 controlParams=None,#控制的維度 type=None)#矩陣的型別
卡爾曼濾波(Kalman Filter)原理與公式推導
公式推導 領域 公式 不一定 技術 精度 原理 應用 定性 一、背景---卡爾曼濾波的意義 隨著傳感技術、機器人、自動駕駛以及航空航天等技術的不斷發展,對控制系統的精度及穩定性的要求也越來越高。卡爾曼濾波作為一種狀態最優估計的方法,其應用也越來越普遍,如在無人機、機器人等領
卡爾曼濾波(Kalman Filter)原理理解和測試
Kalman Filter學原理學習 1. Kalman Filter 歷史 Kalman濾波器的歷史,最早要追溯到17世紀,Roger Cotes開始研究最小均方問題。但由於缺少實際案例的支撐(那個時候哪來那麼多雷達啊啥的這些訊號啊),Cotes
卡爾曼濾波(Kalman Filter)的通俗解釋
假設你有兩個感測器,測的是同一個訊號。可是它們每次的讀數都不太一樣,怎麼辦? 取平均。 再假設你知道其中貴的那個感測器應該準一些,便宜的那個應該差一些。那有比取平均更好的辦法嗎? 加權平均。 怎麼加權?假設兩個感測器的誤差都符合正態分佈,假設你知道這兩個正態分佈的方差,用這兩個方差值,(此處省略若干數學公式
卡爾曼(Kalman)濾波(一)--Kalman濾波的本質
1.Kalman濾波的簡介 接觸過訊號處理的朋友應該清楚,訊號在傳輸過程中必然受到噪聲干擾(外界的二和內部的),使得輸出訊號具有隨機性,為了最大限度降低這種干擾,就需要從混雜在一起的各種訊號中提取自己想要的訊號,這過程稱之為濾波,濾波的方法因訊號而異。
OpenCV之Kalman fileter(卡爾曼濾波)
原理的通俗解釋 用一個網上流傳溫度估計的例子(根據 k-1 時刻的溫度值,估算 k 時刻的是實際溫度值),為了通俗會意,我這裡儘量避免使用專業術語。 假設我們相信溫度是恆定的,所以得到 k 時刻的溫度預測值是跟 k-1 時刻一樣的,假設是23 度,同時該值的高斯噪聲的偏差是 5 度。然後,你
卡爾曼(Kalman)濾波(四)--深入淺出Kalman濾波演算法
Kalman濾波是一種遞迴過程,主要有兩個更新過程:時間更新和觀測更新,其中時間更新主要包括狀態預測和協方差預測,主要是對系統的預測,而觀測更新主要包括計算卡爾曼增益、狀態更新和協方差更新,因此整個遞迴過程主要包括五個方面的計算:1)狀態預測;2)協方差預測;
通俗理解卡爾曼濾波及其演算法實現(帶例項解析)
1.簡介(Brief Introduction) 在學習卡爾曼濾波器之前,首先看看為什麼叫“卡爾曼”。跟其他著名的理論(例如傅立葉變換,泰勒級數等等)一樣,卡爾曼也是一個人的名字,而跟他們不同的是,他是個現代人! 卡爾曼全名Rudolf Emil Kalman,匈牙利數學家,1930年出生於
卡爾曼濾波原理及應用(一)
出於科研需要,打算開始學習卡爾曼濾波(Kalmam Filter)。很早之前就聽說過卡爾曼濾波,但一直沒能深入學習,這次終於有機會了,哈哈。 1.卡爾曼濾波的發展過程 卡爾曼濾波的本質屬於"估計"範疇.先介紹下估計,所謂“估計”問題,就是對收到隨機干擾和隨機測量誤差作用的物理系統,按照某種效
卡爾曼濾波—原理介紹(轉載)
原文連結為:https://blog.csdn.net/heyijia0327/article/details/17487467 這是我看到的寫的比較好的卡爾曼濾波的介紹。 卡爾曼濾波(Kalman filter)是一種高效率的遞迴濾波器(自迴歸濾波器),它能夠從一系列的不完全及包含噪聲的測量中
卡爾曼濾波(一)
舉個例子,上一時刻房間溫度最優值為26度,由於溫度變化緩慢,則可以根據經驗估計本次溫度也為26度,即四式右邊第一項,而此時溫度計讀數為28度,那麼本時刻溫度應該是多少?不知道溫度計精度的情況下,可以對兩個資料求平均,為27度,即T=26+0.5*(28-26)=27。這裡0.5就是本例子中的修正係數,那麼假如
無人駕駛四 擴充套件卡爾曼濾波在目標車輛運動狀態識別中的運用(python程式)
# coding=utf-8 import numpy as np import numdifftools as nd import math dataset = [] # read the measurement data, use 0.0 to stand LI
無人駕駛汽車系統入門(一)——卡爾曼濾波與目標追蹤
前言:隨著深度學習近幾年來的突破性進展,無人駕駛汽車也在這些年開始不斷向商用化推進。很顯然,無人駕駛汽車已經不是遙不可及的“未來技術”了,未來10年
卡爾曼濾波初探(一)
卡爾曼濾波初探 基於時域的線性模型預測 這裡先給出幾個概念(初看的時候很多部落格都沒有這方面說明,若你看到下面懵逼的時候,不妨上來再看看?) 預測:就是根據已有的①經驗、②公式、③以及上一個時間()下檢測物件的狀態的最優估計等資訊,從而得到一個對下一個
無人駕駛汽車系統入門(二)——高階運動模型和擴充套件卡爾曼濾波
前言:上一篇文章的最後我們提到卡爾曼濾波存在著一個非常大的侷限性——它僅能對線性的處理模型和測量模型進行精確的估計,在非線性的場景中並不能達到最優的估計效果。所以之前為了保證我們的處理模型是線性的,我們上一節中使用了恆定速度模型,然後將估計目標的加減速用處理噪聲來表示,這一模
[轉]通俗理解卡爾曼濾波及其演算法實現(例項解析)
1.簡介(Brief Introduction)在學習卡爾曼濾波器之前,首先看看為什麼叫“卡爾曼”。跟其他著名的理論(例如傅立葉變換,泰勒級數等等)一樣,卡爾曼也是一個人的名字,而跟他們不同的是,他是個現代人!卡爾曼全名Rudolf Emil Kalman,匈牙利數學家,19
通俗理解卡爾曼濾波及其演算法實現(例項解析)
1.簡介(Brief Introduction)在學習卡爾曼濾波器之前,首先看看為什麼叫“卡爾曼”。跟其他著名的理論(例如傅立葉變換,泰勒級數等等)一樣,卡爾曼也是一個人的名字,而跟他們不同的是,他是個現代人!卡爾曼全名Rudolf Emil Kalman,匈牙利數學家,19
室內定位系列(五)——目標跟蹤(卡爾曼濾波)
進行目標跟蹤時,先驗知識告訴我們定位軌跡是平滑的,目標當前時刻的狀態與上一時刻的狀態有關,濾波方法可以將這些先驗知識考慮進來得到更準確的定位軌跡。本文簡單介紹卡爾曼濾波及其使用。 原理 這裡僅從目標定位跟蹤的角度做一個簡化版的介紹。 定位跟蹤時,可以通過某種定位技術(比如位置指紋法)得到一個位置估計(
初學者的卡爾曼濾波——擴充套件卡爾曼濾波(一)
簡介 已經歷經了半個世紀的卡爾曼濾波至今仍然是研究的熱點,相關的文章不斷被髮表。其中許多文章是關於卡爾曼濾波器的新應用,但也不乏改善和擴充套件濾波器演算法的研究。而對演算法的研究多著重於將卡爾曼濾波應用於非線性系統。 為什麼學界要這麼熱衷於將卡爾曼濾波器用於非線性系統呢?因為卡爾曼濾波器從一開
慣性導航——擴充套件卡爾曼濾波(一)
對於無人機的慣性導航系統,系統的狀態方程是非線性的,根據擴充套件卡爾曼濾波方程: Predict x^k|k−1Pk|k−1=f(x^k−1|k−1,uk−1)=Fk−1Pk−1|k−1FT