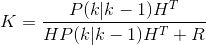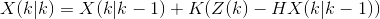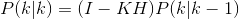Kalman濾波是一種遞迴過程，主要有兩個更新過程：時間更新和觀測更新，其中時間更新主要包括狀態預測和協方差預測，主要是對系統的預測，而觀測更新主要包括計算卡爾曼增益、狀態更新和協方差更新，因此整個遞迴過程主要包括五個方面的計算：1）狀態預測；2）協方差預測；3）卡爾曼增益；4）狀態更新；5）協方差更新；

       用數學公式表示，如下：

狀態預測：

        （1）

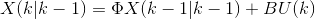
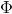
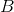
其中，X(k|k)是k時刻的系統狀態，U(k)是k時刻對系統的控制量（如果沒有控制量，可以為零），是狀態轉移矩陣，是系統引數；

主要含義：X(k-1|k-1)是上一狀態的最優結果，X(k|k-1)是利用上一狀態預測得到的結果，這一步主要更新系統結果。

協方差預測：

               （2）

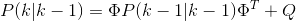
其中，P(k-1|k-1)是上一狀態X(k-1|k-1)對應的協方差，P(k|k-1)是X(k|k-1)對應的協方差，Q是系統過程噪聲（假設為高斯白噪聲）的協方差矩陣；

主要含義：對系統結果對應的協方差進行更新；

計算卡爾曼增益：

其中，K為卡爾曼增益，H為觀測矩陣，R為測量噪聲（同樣假設為高斯白噪聲）對應的協方差矩陣；

主要含義：用於狀態更新和協方差更新中，因為前兩個預測我們得到了當前狀態的預測結果，然後再得到當前狀態的觀測值，通過預測值和觀測值，以及增益，就可以得到當前狀態的最優狀態估計，也就是狀態更新。

狀態更新：

其中，Z(k)是k時刻的觀測值；

主要含義：利用當前狀態的觀測值和預測值，及增益，計算k時刻下的最優狀態估計值X(k|k)，對應著公式（1）中的X(k-1|k-1);

協方差更新：

其中，I為單位矩陣；

主要含義：前面已經更新了狀態，為了保證遞推下去，還要跟新狀態對應的協方差矩陣，對應著公式（2）中的P(k-1|k-1)；

        最後，注意既然是一個遞迴過程，就需要給出引數的初始值，遞迴過程是否很好的收斂取決於初始值的選取，所以要根據實際情況合適選擇。