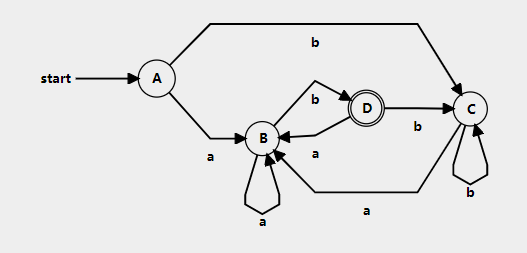
由NFA轉DFA以及DFA的化簡
阿新 • • 發佈:2019-01-12
NFA(Non-deterministic Finite Automata)
不確定有限自動機
構造NFA分成兩步:畫出每一個小單元的NFA;將每一個小單元的NFA組合。
小單元的NFA
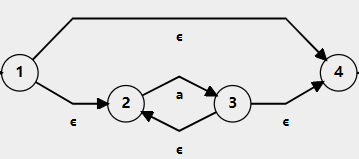
- 單個輸入符號
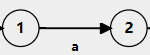
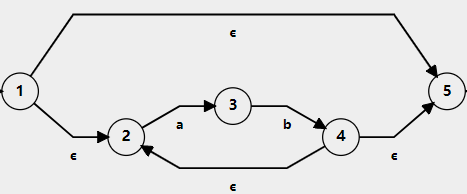
- 連線運算
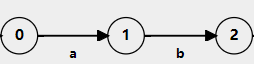
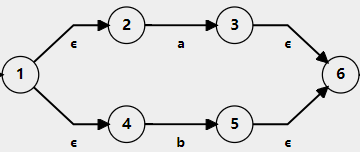
- 選擇運算
新增兩個狀態(選擇運算開始狀態和結束狀態),在開始狀態引兩個路徑通過分別到兩個單輸入符號的NFA,同時兩個NFA都通過到結束狀態。
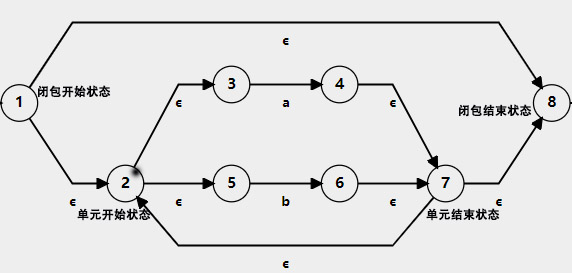
- 閉包運算
新增兩個狀態(閉包運算開始狀態和結束狀態),四條線:閉包運算開始狀態到單元開始狀態;單元結束狀態到閉包運算結束狀態;閉包運算開始狀態到閉包運算結束狀態;單元結束狀態到單元開始狀態。
組合
在組合時,每一個小單元的NFA的開始狀態不變,結束狀態和下一個單元的開始狀態合併。
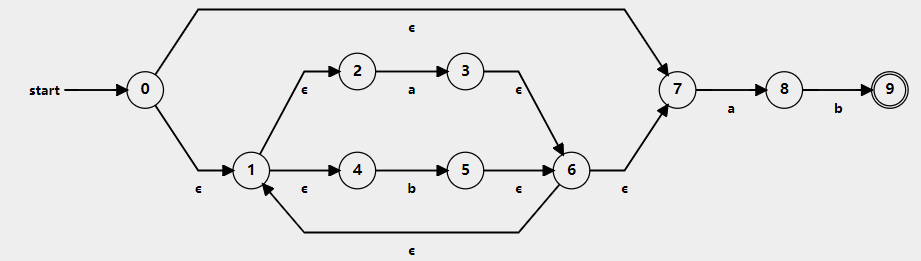
NFA轉DFA(Deterministic Finite Automata)
兩個概念
-:狀態集{1,2,…,n}的閉包。
上式的含義為求1,2,…,n狀態僅通過零個或多個可以到達的所有狀態組成的集合。
:狀態轉換集。
A中的所有狀態通過a可以到達的所有狀態組成的集合。
以為例
- 標記A集合
A集合為開始狀態(即0狀態)的閉包。
如img-7中,0狀態通過可以到達1狀態,7狀態;1狀態通過又可以到達2狀態和4狀態;再加上本身:故A={0, 1, 2, 4, 7}。 - 找出所有的輸入字母
如中,所有的輸入字母為{a, b} - 根據輸入字母尋找A集合的閉包
如img-7中,A集合中遇到a能發生狀態轉變的只有2和7,轉換到狀態3和8,所以={3,8};
然後求-,即-,可以得到結果為{3, 8, 6, 1, 2, 4, 7}=B。
={5},然後求-={5, 6, 1, 2, 4, 7}=C。 - 根據輸入字母尋找所有新產生的集合的閉包
-={1,2,3,4,6,7,8}=B
-={1,2,4,5,6,7,9}=D
-={1,2,3,4,6,7,8}=B
-={1,2,4,5,6,7}=C
-={1,2,3,4,6,7,8}=B
-={1,2,4,5,6,7}=C
包含NFA結束狀態的集合為DFA結束狀態,在例子中D狀態為結束狀態;A狀態為開始狀態。 - 根據以上的計算結果畫出DFA
DFA的化簡
- 加入死狀態
如果一個DFA的轉換函式不是全函式,那麼必須加入一個死狀態,死狀態只有輸入而沒有輸出。例如一個狀態S對a沒有轉換,即move(S,a)=,則-=。 - 把狀態集分為接受狀態集和非接受狀態集
接受狀態集指包含NFA結束狀態的集合;非接受狀態集指不包含NFA結束狀態的狀態集。
例如,在例子中,可以把狀態機劃分為{A,B,C}和{D}。 - 合併不可區分狀態
對上一個步驟中的每一個集合的進行劃分。如果集合中只有一個元素,那就不必再劃分,如{D};如果集合中有多個元素,則尋找哪一個元素經過所有輸入字母的轉換後可以產生非本集合的元素,則將其分離成一個新的集合,如果兩個狀態通過所有的輸入字母都轉換到該集合的元素,那麼它們不必再分。 - 對於上一個步驟中產生的新劃分,重複上一步驟,直至不可再分。
- 如果結果中有死狀態,則去除死狀態,把所有到死狀態的轉換都改為無定義。
栗子
其實可以把劃分的過程看成是一個集合內部排異的過程。
栗子