HDU-1506 Largest Rectangle in a Histogram(單調棧,DP)
Largest Rectangle in a Histogram
Sample Input
7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0
Sample Output
8
4000
題意:
求直方圖中最大的矩形面積
思路:
有兩種解法,個人感覺DP稍簡單一點,單調棧不容易理解。
(一)DP
通過兩次DP,找到每個的左側和右側比本身高的連續的位置,最後去找最大面積。第一遍,先從左到右,然後找每個數的左側,記錄下比本身高的連續的邊界位置,為L。第一遍找到了全部的L。第二遍開始找每個位置的R,從右到左開始,找每個位置的右側比本身高的連續的邊界位置為R。這時每個位置的L,R都求出了。開始判斷最大值。
第一遍找L。
for(int i = 2; i <= n; i++) {
int t = i;
while(t > 1 && a[t-1] >= a[i]) {
t = l[t-1];
}
l[i] = t;
}
第二遍找R.
for(int i = n-1; i >= 1; i--) {
int t = i;
while(t < n && a[t+1] >= a[i]) {
t = r[t+1];
}
r[i] = t;
}
程式碼:
#include<bits/stdc++.h> (二) 單調棧
單調棧的思想是:用一個棧來儲存下標,遇到比棧中下標對應的值大的高度時,這時把這個下標進棧,保證棧中下標的高度為遞增的(可以相等)。遇到比棧中下標對應值小的高度時,出棧並就計算面積(也就是棧頂元素的高度*(i-出棧後的棧頂-1),非空棧時),如果i == n時,且為空棧時這時面積為(height[棧頂] * i),和res比較,取最大值。
為了保證有結束狀態,要在最後中壓入一個0,height[n] = 0;
看例子比較清晰:
height=[2,1,5,6,2,3]
- 剛開始棧為空,壓入下標0;當i=1時,不滿足height[1] >= height[0],下標出棧,棧為空,計算面積res = height[0](1-0) = 2;
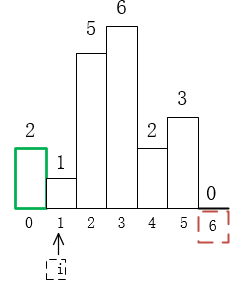
2)高度1,5,6為依次遞增的,所以對應下標依次壓棧;此時棧元素有(1,2,3)。當i = 4時,不滿足height[4] >= height[3],所以此時棧頂元素3出棧,計算此時面積res = height[3](4-3)=6。
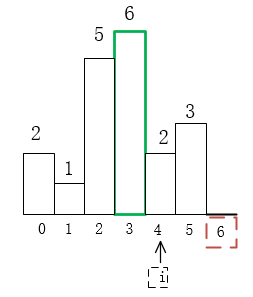
3)當前棧為(1,2),棧頂為2,i=4,不滿足height[4] >= height[2],所以棧頂2出棧,計算此時面積res=height[2]*(4-2)=10
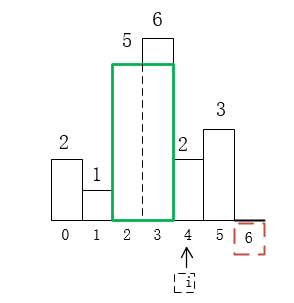
4)當前棧為(1),棧頂為1,i=4,滿足height[4] >= height[1],所以i=4進棧,i++;棧為(1,4), i=5時,滿足height[5] >= height[4],所以5進棧,棧為(1,4,5),i++;i=6,此時height[6]=0,不滿足height[6] >= height[5],5出棧,計算面積res=(6-5)*height[5]=3;
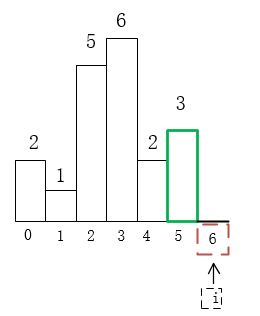
5)當前棧為(1,4),棧頂為4,i=6,不滿足height[6] >= height[4],所以4出棧,計算面積res=(6-4)*height[4]=4;
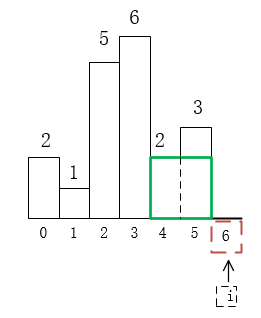
6)當前棧為(1),棧頂為1,i=6,不滿足height[6] >= height[1],所以1出棧,此時為空棧,這次計算面積比較特殊res=height[1]n=16=6;

參考部落格:https://www.cnblogs.com/love-yh/p/7182920.html
程式碼:
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1000005;
long long height[maxn];
int main()
{
int n;
while(cin >> n && n) {
for(int i = 0; i < n; i++){
cin>>height[i];
}
height[n] = 0;
stack<int> s;
long long maxx = 0; //這裡一定要maxx = 0 否則錯。。。。
long long sum = 0;
for(int i = 0; i <= n; ++i) {
if(s.empty() || (height[s.top()] <= height[i])) {
s.push(i);
}
else {
long long p = s.top();
s.pop();
if(s.empty())
sum = height[p]*i;
else
sum = height[p]*(i-s.top()-1);
if(sum >= maxx)
maxx = sum;
--i;
}
}
cout << maxx << endl;
}
return 0;
}
相關推薦
HDU-1506 Largest Rectangle in a Histogram(單調棧,DP)
Largest Rectangle in a Histogram Sample Input 7 2 1 4 5 1 3 3 4 1000 1000 1000 1000 0 Sample Output 8 4000 題意: 求直方圖中最大的矩形面積 思路:
HDU - 1506 Largest Rectangle in a Histogram (單調棧/笛卡爾樹)
return col 一道 scan 卡爾 左右 build new \n 題意:求一個直方圖中最大矩形的面積。 很經典的一道問題了吧,可以用單調棧分別求出每個柱子左右兩邊第一個比它低的柱子(也就相當於求出了和它相連的最後一個比它高的柱子),確定每個柱子的左右邊界,每個柱
POJ 2559 &&HDU 1506 Largest Rectangle in a Histogram && 51nod 1102 面積最大的矩形 單調棧的應用
題目大意:POJ 2559 &&HDU 1506 && 51NOD 1102這三個題其實都是一個題,有N個矩形,寬度都為1,給出N個矩形的高度,求由這N個矩形組成
hdu-1506-Largest Rectangle in a Histogram(dp)
題目:http://acm.hdu.edu.cn/showproblem.php?pid=1506 題意:給出一個n個寬為1的長方形,之後給出第i個長方形的高a[i]。求出由n個長方形組成的圖形所能構成的面積最大的長方形。 這道題曾經用單調棧做過,想了解的
POJ-2559 Largest Rectangle in a Histogram(單調棧)
comm pict mon include max specified out names align Largest Rectangle in a Histogram Time Limit: 1000MS Memory Limit: 65536K Tota
POJ 2559 - Largest Rectangle in a Histogram - [單調棧]
style long push += cst tac ++ tar 開始 題目鏈接:http://poj.org/problem?id=2559 題意: 給出 $n(1 \le n \le 10^5)$ 個寬為 $1$,高為 $h_i(0 \le h_i \le 10^
POJ2559 Largest Rectangle in a Histogram(單調棧)
題意: 給出一組矩形的高,求最多能拼成矩形的最大面積,看圖就很清楚了。 要點: 還是單調棧,現在有點感覺了,單調棧大概就是能求出當前值左右的比它大或小的數的範圍。這題用高度作為單調棧,分別往左右找比當
HUD 1506 Largest Rectangle in a Histogram(單調棧的應用)(題目詳解)
A histogram is a polygon composed of a sequence of rectangles aligned at a common base line. The rectangles have equal widths but may have different height
HUD 1506 Largest Rectangle in a Histogram
problem ssi member img 個數 accept fin character ref Largest Rectangle in a Histogram Time Limit: 2000/1000 MS (Java/Others) Memory Lim
POJ2559 Largest Rectangle in a Histogram 單調隊列
sta eight 所有 for 我們 return rec += std 題目大意 有一個直方圖,其所有矩形的底均是1(以後簡稱小矩形)。給出這些矩形的高度,求這些矩形的並集中存在的面積最大的矩形(簡稱大矩形)的面積。 題解 大矩形的高必然一邊等於一個小矩形的高,
HDU1506 / POJ2339 Largest Rectangle in a Histogram 單調遞減棧
1.什麼是單調棧 具有單調性和棧的性質 單調遞減棧就是從棧底到棧頂是單調遞減的 單調遞增棧就是從棧底到棧頂是單調遞增的 2.單調棧解決的問題 以自己為最小值,找到最長的區間;單調遞增棧 以自己為最大值,找到最長的區間;單調遞減棧 給定一個區間找到這個區間的最大值或
Largest Rectangle in a Hitogram-單調棧の入門好題
單調棧的好題 題目連結 題目是求最大矩形面積 1.BF思路 可以想到最後大矩形的上邊界一定是某個小矩形的頂 那麼我們就列舉每一個小矩形, 將其頂作為限制條件儘可能地向兩邊擴充套件 複雜度\(O(n^2)\) 2.單調棧做法 如圖,黑色為最終要求的矩形 我們可以維護一個單調遞增棧
POJ2559--Largest Rectangle in a Histogram(棧)
題目大意:有n個寬為1,高為h1,h2,h3...hn的長方形從左到右依次排列,形成一個柱狀圖,求最大矩形面積 分析:運用棧來求解。 首先,我們可以得到這樣一個事實,假設最大的矩形的兩個端點為L[i
POJ 2559 Largest Rectangle in a Histogram(單調棧)
common pst locale str flow bold text function target 【題目鏈接】:click here~~ 【題目大意】: A histogram is a polygon composed of a sequence of
題解報告:poj 2559 Largest Rectangle in a Histogram(單調棧)
++i char test case c代碼 ams pac 分享圖片 cas ram Description A histogram is a polygon composed of a sequence of rectangles aligned at a common
E - Largest Rectangle in a Histogram POJ - 2559 -單調棧第二彈
E - Largest Rectangle in a Histogram POJ - 2559 維護一個非遞增單調棧,對於每個矩形,我們求出它向左向右分別能延伸的長度,然後乘以它的高度。 這就是以當前矩形為最低高度可以得到的最大
2559 Largest Rectangle in a Histogram【單調棧】
Time limit 1000 ms Memory limit 65536 kB A histogram is a polygon composed of a sequence of rectangles aligned at a common base lin
【poj 2559 Largest Rectangle in a Histogram】【單調棧】
【連結】 【題意】 在一條水平線上有若干緊挨的矩形,求包含於這些矩形的並集內部的最大的矩形的面積(矩形個數<=1e5) 【分析】我們先考慮,若矩形的高度從左往右單調遞增,那麼答案顯而易見嘗試以每個矩形的高度為最終矩形的高度,並把寬度延伸到右邊界,得到一個矩形,
POJ 2559-Largest Rectangle in a Histogram 解題報告 【笛卡爾樹與單調棧】
POJ 2559-Largest Rectangle in a Histogram 解題報告 【笛卡爾樹與單調棧】 Description A histogram is a polygon composed of a sequence of rectang
【單調棧】hdu1506 Largest Rectangle in a Histogram ----簡單瞭解單調棧
這個題是可以用動態規劃,或者是單調棧、其實實質是差不多的; 1. 什麼是單調棧 單調棧就是保持了單調性和棧的性質; 單調遞增的棧就是從棧尾到棧頂是單調遞增的; 2. 單調棧能夠解決的問題 1) 以
