c++實現簡單選擇排序和堆排序
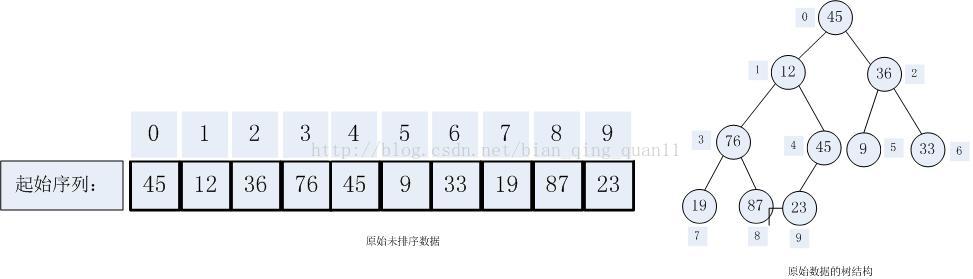
接下來我們對簡單選擇排序和堆排序做詳細額介紹,排序過程中使用的資料仍和前兩節排序過程中使用的資料相同:int a[10] = {45,12,36,76,45,9,33,19,87,23};
1、簡單選擇排序
1.1 簡單選擇排序的基本思想
簡單選擇排序的基本思想就體現在“選擇”這兩個字上,每一趟排序都是從沒有排序的資料中選出最小的元素與第一個資料進行交換。給定一個有n個數據的陣列,演算法的執行步驟如下:
(1)從左到右遍歷整個資料,從陣列中選出最小的元素;
(2)如果選出的最小元素不在第一個位置,將整個最小元素與第一個位置資料進行交換;
(3)對剩餘的n-1個數執行(1),(2)的操作;
1.2 實現程式碼
1.3 排序結果#include<iostream> using namespace std; void searchSort(int *a, int n) { for (int i = 0; i < n - 1; ++i) { int indexSmallestEle = i; for (int j = i; j < n; ++j)//尋找後面的最小的資料 { if (a[j] < a[indexSmallestEle]) { indexSmallestEle = j; } } if (indexSmallestEle != i) { int temp = a[i]; a[i] = a[indexSmallestEle]; a[indexSmallestEle] = temp; } } } int main() { int a[10] = { 45, 12, 36, 76, 45, 9, 33, 19, 87, 23 }; searchSort(a, 10); return 0; }
1.4 演算法分析
由於簡單選擇排序每一次都是從待排序資料中選擇出一個最小的元素與第一個位置發生交換,每次確定一個元素的最終位置。有n個元素的話,經過n-1趟排序就能達到最終排序效果。
第一趟排序要比較n個數據,篩選出最小的;第二趟排序要比較n-1個數據,篩選最小的;,....,第n-1次要比較2個數據。這樣簡單選擇排序的時間為n + n-1 + n-2 + ... + 2,不會出現最好的最壞情況,因此時間複雜度為O(n^2)。
1.5 穩定性
不穩定。
例如{ 2, 2, 1}, 第一次選的時候變成 { 1, 2, 2 }, 兩個2的次序就變了。
2、堆排序
2.1 堆排序的基本思想
首先我們要知道堆的含義。這裡做一個簡單的回顧,我們所說的對一般是指二叉堆(當然還有其他的堆,如斐波那契堆),本質是一顆完全二叉樹,要求樹中每個非葉節點的值要大於等於(或者小於等於)他的孩子節點的值,這樣的堆叫作大頂堆(小頂堆)。堆排序就是給定一組數,我們將這組數按從左到右的順序構造一顆完全二叉樹,然後調整樹中元素的位置使其滿足大頂堆(小頂堆)的性質,就完成了對排序。
本文中我們以大頂堆為例來對陣列int a[10] = {45,12,36,76,45,9,33,19,87,23} 進行排序。將該資料建立完全二叉樹後,下標為i的節點的左孩子下標是2i + 1,右孩子下標為 2i + 2。而下標為i的節點的父節點為(int)((i-1)/2)。陣列a對應的初始完全二叉樹如下圖(其中二叉樹中每個節點的旁邊數字是該節點在陣列中的下標):
2.2 實現程式碼
#include<iostream>
using namespace std;
void fixHeap(int *a, int p, int n)//對陣列中下標為p的資料進行調整
{
if (p <= (n - 1) / 2)//下標為p點不是一個葉子節點
{
int largestIndex = p;
if (2 * p + 1 <= n - 1)
{
if (a[2 * p + 1] > a[p])
{
largestIndex = 2 * p + 1;
}
}
if (2 * p + 2 <= n - 1)
{
if (a[2 * p + 2] > a[largestIndex])
{
largestIndex = 2 * p + 2;
}
}
if (largestIndex != p)
{
int temp = a[p];
a[p] = a[largestIndex];
a[largestIndex] = temp;
fixHeap(a, largestIndex, n);
}
}
else
{
return;
}
}
void heapSort(int *a, int n)//從倒數第一個非葉節點開始,從下到上進行調整
{
for (int i = (n - 1) / 2; i >= 0; --i)
{
fixHeap(a, i, n);
}
}
void print(int *a, int n)
{
for (int i = 0; i < n; ++i)
{
cout << a[i] << " ";
}
cout << endl;
}
int main()
{
int a[10] = { 45, 12, 36, 76, 45, 9, 33, 19, 87, 23 };
cout << "排序前:";
print(a, 10);
heapSort(a, 10);
cout << "排序後:";
print(a, 10);
return 0;
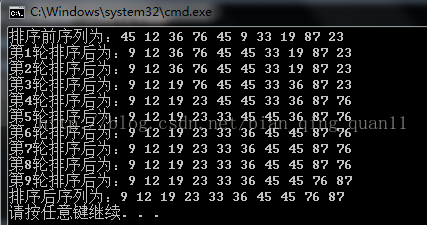
}2.3 排序結果
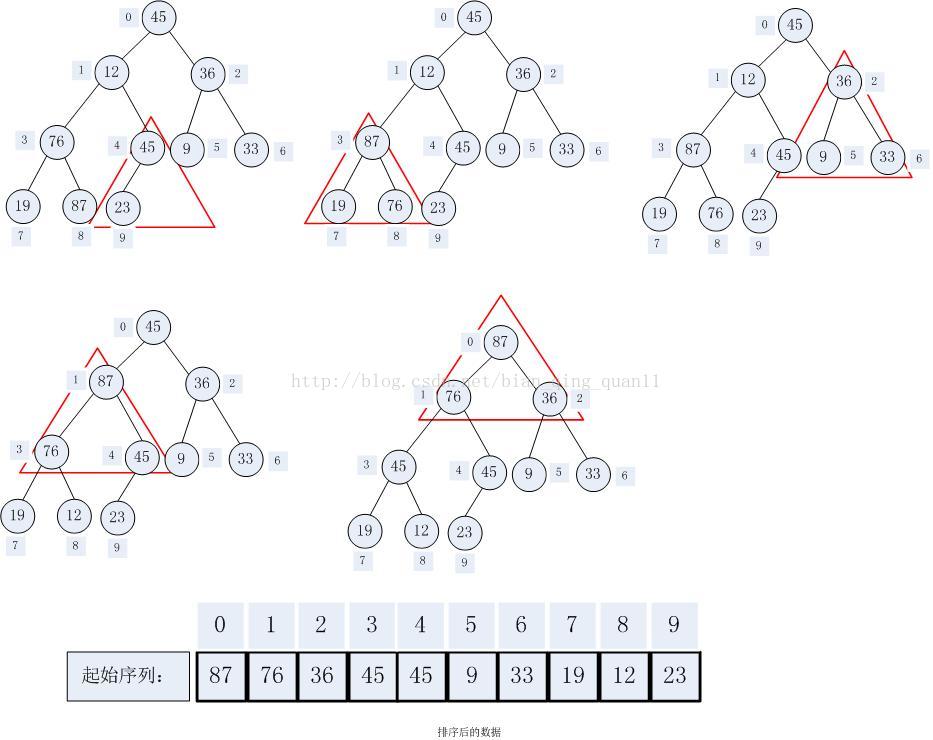
排序的最終結果為:
排序過程:整個堆排序是一個從下往上的調整過程,對每一個調整又是從當前位置開始往下調整的過程。
2.4 演算法分析
由演算法產生的結果可知,堆排序並不能將陣列中的資料按照完全的降序,而只是滿足了大頂堆的性質(每個節點值都大於孩子節點的值)。由於建初始堆所需的比較次數較多,所以堆排序不適宜於記錄數較少的檔案,平均時間複雜度為O(n*logn).
2.5 穩定性
不穩定。
2.6 堆排序用途
輸入M個數,從中找出前K個最小的數並保持有序。
這裡使用堆排序是個不錯的選擇,使用輸入的前K個數建立一個大頂堆。對於後面的數,每輸入一個數據就與堆頂元素進行比較,如果大於堆頂元素,繼續輸入;如果小於堆頂元素,則將該輸入資料設為堆頂資料,然後通過調整構成新的大頂堆。這樣遍歷一遍M個數據就可以找到K個最小數。
相關推薦
c++實現簡單選擇排序和堆排序
接下來我們對簡單選擇排序和堆排序做詳細額介紹,排序過程中使用的資料仍和前兩節排序過程中使用的資料相同:int a[10] = {45,12,36,76,45,9,33,19,87,23}; 1、簡單選
排序演算法(四)、選擇排序 —— 簡單選擇排序 和 堆排序
1、簡單選擇排序簡單選擇排序思想是:從頭到尾(從後往前也行)遍歷序列,先固定第一個位置的資料,將該位置後面的資料,依次和這個位置的資料進行比較,如果比固定位置的資料大,就交換。這樣,進行一趟排序以後,第一個位置就是最小的數了。然後重複進行,第 2 次遍歷並且比較後,第二個位置
排序演算法(1):簡單選擇排序和堆排序
1.簡單選擇排序 (1)本質:每一趟從給定待排序序列A[ 1......n ] ,選擇出第i小元素,並和A[i]交換。 程式碼: /************************************************* 演算法:簡單選擇排序(升序) 時間
算法2 排序算法:直接選擇排序和堆排序
重新 父親 i++ 快速排序 selection left http edi spl 上一篇總結了交換排序的冒泡排序和快速排序。這一篇要總結的是選擇排序,選擇排序分為直接選擇排序和堆排序,主要從以下幾點進行總結。 1、直接選擇排序及算法實現 2、堆排序及算法實現
演算法02 七大排序之:直接選擇排序和堆排序
上一篇總結了交換排序的氣泡排序和快速排序。這一篇要總結的是選擇排序,選擇排序分為直接選擇排序和堆排序,主要從以下幾點進行總結。 1、直接選擇排序及演算法實現 2、堆排序及演算法實現 1、直接選擇排序及演算法實現 直接選擇排序(Straight Select S
資料結構和算法系列6 七大排序之直接選擇排序和堆排序
上一篇我們總結了交換排序的氣泡排序和快速排序。那麼這一篇我們要總結的是選擇排序,選擇排序分為直接選擇排序和堆排序,我們主要分以下幾點進行總結。 1,直接選擇排序及演算法實現 2,堆排序及演算法實現 1,直接選擇排序及演算法實現 直接選擇排序(Straight Select Sort)是一種簡單的排序方法,它
歸並排序和堆排序
pso 結構 key 空間 歸並算法 順序存儲 構造 [ ] 向上 知識點總結報告 知識點: 歸並排序 (原理)歸並排序是多次將兩個或兩個以上的有序表合並成一個新的有序表。最簡單的歸並是直接將兩個有序的子表合並成一個有序的表,即二路歸並。 二路歸並排序基本思路是將R[0..
用c#實現簡單的登入和註冊功能
這兩天c#大作業要求做一個簡單的通訊錄系統,我就先做了登入和註冊的功能,在網上看了一些程式碼,自己再做,終於做出來了。做的不是很美觀,但是可以簡單實現。 首先用sqlserver建表。我建了一個名為user_info的表,新增username和passdwo
排序演算法之希爾排序和堆排序
希爾排序簡述: 希爾排序可以看作是直接插入排序的一種優化,即把一個數插入一個有序表,不過希爾排序多了一個預設的增量,把一個序列分成若干個增量大小的增量序列,然後在子序列直接進行直接插入排序,每次都使較
快速排序和堆排序代碼
調用 兩種 ++ null base uic flag arr ase 最近復習到快速排序和歸並排序,根據其排序思路,自己動手實現了一下,這兩種排序都用到了遞歸調用,在以往的項目中沒有用到過遞歸,所以這次趁此機會練習下遞歸的使用。 快速排序 /** * 快速排序 * @
C語言中常用排序演算法(氣泡排序、選擇排序、插入排序、希爾排序、快速排序、堆排序)實現比較
以下程式在win10 X64位作業系統,使用VS2017執行驗證可行 排序是非常重要且很常用的一種操作,有氣泡排序、選擇排序、插入排序、希爾排序、快速排序、堆排序等多種方法。 例項1 冒泡法排序 1.前言: 陣列中有N個整數,用冒泡法將它們從小到大(或從大到小)排序。冒泡法
(資料結構排序的實驗四)快速,冒泡,簡單選擇,直接插入排序的c語言實現!!
<span style="font-size:18px;"><span style="font-size:18px;"><span style="font-size:18px;"><span style="font-size:18p
C語言簡單選擇排序演算法的實現
簡單選擇排序從元素中跳出最小關鍵字,將其放在已排序列的最後,未排序的序列最前,直到全部排序完成為止,其空間複雜度為O(1),時間複雜度為O(n2)。下面是實現程式碼: 首先仍然是預定義和型別定義: #define OK 1 #define ERROR 0 typedef
用Java實現的選擇排序和冒泡排序
auth main sta -i str public java index 選擇 選擇排序 package cn.hxd.sort; /** * 選擇排序 * @author Administrator * */ public class SelectionSo
C#實現簡單的冒泡排序
read pro i++ cto bsp con nbsp ces nag 1、C#代碼下:using System;namespace ConsoleApplication1{ class Program { static void Main()
《C語言》氣泡排序、快速排序、選擇排序、堆排序、桶排序、插入排序。
氣泡排序、快速排序、選擇排序、堆排序、桶排序、插入排序。 Main.c MySort.h MySort.c Main.c #include <time.h> #include "MySort.h" #define N 10
排序 (2) -----簡單選擇排序和氣泡排序
簡單選擇排序和氣泡排序 兩種方法都是每一趟找出最大(小)的他放在一個位置,下一趟不用去管這個位置,只是兩種方法採用的找的形式不一樣 1. 簡單選擇排序:固定位置與前(後)面的比較 例子:5 1 6 2 假如按從小到大排序 5:粗體標記表示 固定的位置 5:這種標記表示已經排好
Java實現快速排序、歸併排序、堆排序和希爾排序
快速排序 演算法思想 1.將陣列的第一個元素取為target,定義兩個指標i 和 j; 2.指標i ,從左向右找到第一個比target大的元素,指標j從右向左找到第一個比target小的元素,
C#選擇排序和氣泡排序
在上一篇文章中《演算法排序》中簡單介紹了選擇排序和氣泡排序,這次讓咱們緊接著上次的節奏繼續來學習這兩種排序。都說是萬事開頭難,其實有了充分的準備一點都不難了,在本文中,小編將要介紹演算法排序的圖形過程
常用內部排序演算法之四:簡單選擇排序、直接插入排序和氣泡排序
前言 之所以把這三類演算法放在一塊,是因為除此之外的演算法都是在這三類演算法的基礎上進行優化的。簡單選擇排序的思想是每一趟n−i+1(i=1,2,...,n−1)個記錄中選擇最小的記錄作為有序序列的第i個記錄。直接插入排序的思想是將一個記錄插入到已經排好序的有