知乎--LSTM(挺全的)
最近接到指導老師給的“看一下LSTM”的任務。
雖然之前已經瞭解過LSTM以及RNN的基本原理和適用範圍,但是還沒有寫過程式碼,因此通過這個機會,將RNN以及LSTM及其變體,更詳細的瞭解一下,並儘量將其實現。
Below comes from Wikipedia:
遞迴神經網路(RNN)是兩種人工神經網路的總稱。一種是時間遞迴神經網路(recurrent neural network),另一種是結構遞迴神經網路(recursive neural network)。時間遞迴神經網路的神經元間連線構成有向圖,而結構遞迴神經網路利用相似的神經網路結構遞迴構造更為複雜的深度網路。
不做特別說明,本文中我使用 RNN 指代 Recurrent Neural Network,或迴圈神經網路。
RNN 可以描述動態時間行為,因為和前饋神經網路(feedforward neural network)接受較特定結構的輸入不同,RNN將狀態在自身網路中迴圈傳遞,因此可以接受更廣泛的時間序列結構輸入。手寫識別是最早成功利用RNN的研究結果。
Tomas Mikolov 和 Martin Karafiat 在 2010 年提出了一個 rnn based language model。這個語言模型主要被應用在兩個方面:
- 對任意一個 sentence,我們可以根據其在現實世界中出現的可能性來給其打分。這就給我們了一種用來衡量語法和語義準確性的準則。基於 RNN 的語言模型已經被廣泛應用在機器翻譯中,前幾天 Google 釋出的 GNMT,就是基於 LSTM 的改進,而 LSTM 則是基於 RNN。
- 一個語言模型(language model)使我們可以用來生成新文字。最近在微博上看到了很多利用 RNN 來寫詩等的有趣應用,比如學習汪峰作詞,學習李商隱寫詩……
在傳統的神經網路中,輸入和輸出一般是相互獨立的。RNNs 的核心思想就是怎樣利用輸入的 sequential information。比如,在詞序的預測中,我們要預測下一個單詞,那就需要根據它前面的單詞來推測當前的單詞可能是什麼。
RNNs 的 recurrent 表示 它對序列中的每個元素都執行同樣的 task,每個 element 計算的輸出依賴於之前的計算結果。更形象一點地說,RNNs 有了 ’memory‘,它可以捕捉到目前為止已經得到的資訊。理論上,RNNs 是可以用於任一長度的序列的,但是實際上,它們只對前幾步有比較好的記憶效果。
一個 RNN 的結果如下圖所示,把它展開,就是右邊的樣子,他們的內部結構是完全一樣的。箭頭表示時間序列/輸入序列。圖片來源於 Nature。
舉例來說,如果我們輸入了一個長度為 5 個單詞的句子,那這個 RNN 展開之後就是一個 5 層的神經網路,每層處理一個 word。
x 表示每一層的輸入,s 表示 hidden state,這就是前面說到的 ’memory‘,它通過 x 和 上一層的 s 計算得到,計算的函式是一個非線性函式,比如 tanh 或者 ReLU。第一層的 hidden state 通常被初始化為 0。 o 表示輸出。例如如果我要預測一句話的下一個詞是什麼,那這個輸出就是基於自定義的 vocabulary 的概率分佈。我們可以使用 softmax 函式來計算得到輸出。
Someting to NOTE:
- captures information about what happened in all the previous time steps. The output at step is calculated solely based on the memory at time .
- a traditional deep neural network, which uses different parameters at each layer, a RNN shares the same parameters (U,W,V above) across all steps.This reflects the fact that we are performing the same task at each step, just with different inputs.
- There’re outputs at each time step, but depending on the task this may not be necessary. Similarly, we may not need inputs at each time step.The main feature of an RNN is its hidden state, which captures some information about a sequence.
目前 RNNs 被廣泛應用於 NLP 領域,而現在絕大多數的 RNNs Model 都是 LSTMs。在瞭解 LSTM 之前,先看一下 RNNs 在 NLP 領域應用的一些例子:
3. 如何訓練 RNNs?同樣是使用 BP 演算法,不過有點不同:Backpropagation Through Time (BPTT)。前面提到,由於 RNNs 中的引數是網路中的所有 time steps 共享的,所以我們計算當前步的梯度時,也需要利用前一步的資訊。例如,我們計算 t=4 的梯度時,我們需要反向傳播到前一步,然後將它們的梯度相加。在更深入的瞭解之前,需要明確的是, BPTT 在學習 long term dependencies 的時候是有困難的。這個問題被稱作 ’Vanishing/Exploding gradient problem‘。這個問題一般是指我們常說的 vanilla RNNs。
4. A brief overview of RNNs Extensionsvanilla是什麼意思呢?
“Vanilla” is a common euphemism(委婉語) for “regular” or “without any fancy stuff.”
類似於 naive
-
Bidirectional RNNs
They are based on the idea that the output at time may not only depend on the previous elements in the sequence, but also future elements.
They are just two RNNs stacked on top of each other. The output is then computed based on the hidden state of both RNNs.
-
Deep (Bidirectional) RNNs
They are similar to Bidirectional RNNs, only that we now have multiple layers per time step. In practice this gives us a higher learning capacity (but we also need a lot of training data).
-
LSTM networks
They use a different function to compute the hidden state. The memory in LSTMs are called cellsand you can think of them as black boxes that take as input the previous state and current input . Internally these cells decide what to keep in (and what to erase from) memory. They then combine the previous state, the current memory, and the input. It turns out that these types of units are very efficient at capturing long-term dependencies.
在此使用 Python 實現了一個全功能的 RNN,並用 Threano 進行 GPU 加速。完整的程式碼在我的 Github。
-
Language Modeling
我們的目標是用 RNN 搭建一個 Language Model。話句話說,我們有一個 m 個單詞的句子,語言模型可以讓我們預測被觀測 sentence 在給定的 dataset 中的概率。
基於貝葉斯理論,我們有:
在單詞層面,一句話的概率就是每個單詞在給定之前單詞時出現概率的乘積。舉個例子來說,“He went to buy some chocolate.” 的概率就是在給定 “He went to buy some” 時,“chocolate”出現的概率乘以給定 “He went to buy”時 “some” 出現的概率乘以 …… 以此類推。
但這為什麼會管用呢 ?為什麼我們要給一個句子加上概率分佈?
- 首先,這種模型可以被用作一個打分機制(scoring mechanism)。例如,一個 MT 系統一般對一個輸入會產生多個可選值。這是你就可以使用一個語言模型來選出概率最大的句子。直覺上來說,最可能的句子也更可能是語法正確的。在語音識別系統中也有類似的打分機制。
- 解決這種語言模型問題也會有一個很酷的副作用。因為我們能根據給定的前置詞序列預測一個單詞的概率,所以我們可以用它來生成新文字。這就是一個生成式的模型。大神Andrej Karparthy 有一篇文章 解釋了語言模型的這種能力。——— Mark———(還沒看)
在上面的等式中,每個 word 都是需要它之前的所有詞的,但是在實際中,很多模型在表示這種長距離依賴的時候有些問題。導致這些問題的原因有太耗費計算資源,或者記憶體不足等。所以,RNNs 一般只會 look 當前詞之前的幾個詞。當然實際操作會更復雜一點。稍後就會講到。
-
訓練資料集 及 預處理
為了訓練我們的 language model,我們當然需要一些資料用來學習。幸運的是,訓練語言模型並不需要 labels,只需要 raw data 就可以。此處使用的資料集是 15000 個稍長的 紅迪網的評論,在此。用稍後我們搭建的模型生成的一句跟真正的評論員很像。在那之前,我們需要先對資料做一些預處理,使其符合我們的需要的格式。
-
Tokenize text
我們需要將評論分成單個的句子,然後分成單個的 word。這裡我們使用的 NLTK 的 word_tokenize 和 sent_tokenize 方法。
-
去掉詞頻很低的詞
大多數詞只出現了一兩次,將這些詞語去掉可以讓我們的模型訓練的更加快速。由於對這些詞我們並沒有很多上下文的例子,所以我們也不能用它們來學習如何正確的使用這些詞頻很低的詞。這根人學習的過程是很詳細的。如果想要知道如何正確的使用某個詞,我們需要在不同的上下文環境中體會它們使用上的差別。 在程式碼中,將 vocabulary 限制到了 **vocabulary_size** 個最常見的單詞。並將所有不在我們的 vocabulary 中的單詞 設定為 **UNKOWN_TOKEN**。將其跟其他單詞同樣看待,在訓練結束後如果有 UNKOWN_TOKEN,要麼將其隨機換成不在 vocabulary 中的詞,要麼繼續訓練只生成不含 UNKOWN_TOKEN 的句子。 -
為每句話新增 SENTENCE_START 和 SENTENCE_END
這樣做的意義在於,如果給的是 SENTENCE_START,它的下一個單詞可能是什麼。也就是,如何生成每句話第一個真正的 word。 -
建立 訓練資料矩陣
輸入到 RNN 中的是向量,不是字串。因此向其他文字處理的模型一樣,我們先建立 word 和 index/id 之間的對映關係:index_to_word 和 word_to_index。 For example, the word “friendly” may be at index 2001. A training example  may look like `[0, 179, 341, 416]`, where 0 corresponds to `SENTENCE_START`. The corresponding label 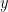 would be `[179, 341, 416, 1]`. Remember that our goal is to predict the next word, so y is just the x vector shifted by one position with the last element being the `SENTENCE_END` token. In other words, the correct prediction for word `179` above would be `341`, the actual next word.vocabulary_size = 8000 unknown_token = "UNKNOWN_TOKEN" sentence_start_token = "SENTENCE_START" sentence_end_token = "SENTENCE_END" # Read the data and append SENTENCE_START and SENTENCE_END tokens print "Reading CSV file..." with open('data/reddit-comments-2015-08.csv', 'rb') as f: reader = csv.reader(f, skipinitialspace=True) reader.next() # Split full comments into sentences sentences = itertools.chain(*[nltk.sent_tokenize(x[0].decode('utf-8').lower()) for x in reader]) # Append SENTENCE_START and SENTENCE_END sentences = ["%s %s %s" % (sentence_start_token, x, sentence_end_token) for x in sentences] print "Parsed %d sentences." % (len(sentences)) # Tokenize the sentences into words tokenized_sentences = [nltk.word_tokenize(sent) for sent in sentences] # Count the word frequencies word_freq = nltk.FreqDist(itertools.chain(*tokenized_sentences)) print "Found %d unique words tokens." % len(word_freq.items()) # Get the most common words and build index_to_word and word_to_index vectors vocab = word_freq.most_common(vocabulary_size-1) index_to_word = [x[0] for x in vocab] index_to_word.append(unknown_token) word_to_index = dict([(w,i) for i,w in enumerate(index_to_word)]) print "Using vocabulary size %d." % vocabulary_size print "The least frequent word in our vocabulary is '%s' and appeared %d times." % (vocab[-1][0], vocab[-1][1]) # Replace all words not in our vocabulary with the unknown token for i, sent in enumerate(tokenized_sentences): tokenized_sentences[i] = [w if w in word_to_index else unknown_token for w in sent] print "\nExample sentence: '%s'" % sentences[0] print "\nExample sentence after Pre-processing: '%s'" % tokenized_sentences[0] # Create the training data X_train = np.asarray([[word_to_index[w] for w in sent[:-1]] for sent in tokenized_sentences]) y_train = np.asarray([[word_to_index[w] for w in sent[1:]] for sent in tokenized_sentences])經過處理後的 training example 像下面這樣:x: SENTENCE_START what are n't you understanding about this ? ! [0, 51, 27, 16, 10, 856, 53, 25, 34, 69] y: what are n't you understanding about this ? ! SENTENCE_END [51, 27, 16, 10, 856, 53, 25, 34, 69, 1] -
構造 RNN
前面已經瞭解了 RNN 的結構,這裡我們開始具體介紹這裡的模式是怎樣的。 輸入 x 是一個 sequence of words,x 的每個元素都是一個單詞。但是這裡我們還有一件事要做。由於據陳懲罰的機理限制,我們不能直接使用單詞的 index 作為輸入,而是使用 vocabulary_size 大小的 one-hot vector。也就是說,每個 word 都變成了一個 vector,這樣輸入 x 也就變成了 matrix,這時每一行表示一個word。我們在神經網路中執行這一轉換,而不是在之前的預處理中。同樣的,輸出 o 也有類似的格式,o 是一個矩陣,它的每一行是一個 vocabulary_size 長的 vector,其中每個元素代表其所對應的位置的所對應的單詞表中的單詞在輸入的這句話中,出現在下一個待預測位置的概率。 我們先回顧一下 RNN 中的等式關係:  在推倒過程中寫下矩陣和向量的維度是一個好習慣,我們假設選出了一個 8000 個詞的 vocabulary。 Hidden layer 的 size H = 100。這裡的 hidden layer size 可以看做是我們的 RNN 模型的 “memory”。增大這個值標表示我們可以學習更加複雜的模式。這也會導致額外的計算量。現在我們有如下變數:  這裡的 U, V, W 都是我們的神經網路需要學習的引數。因此,我們一共需要 2HC + H^2 = 2\*100\*8000 + 100\*100 = 1,610,000。溫度也告訴我們了我們的模型的瓶頸在哪裡。由於 x_t 是 獨熱編碼的向量,將它與 U 相乘本質上等同於選擇 U 的一列,所以我們不需要做全部的乘法。還有,我們的網路中,最大的矩陣乘法是 V.dot(s_t). 這就是我們儘可能讓我們的 vocabulary size 儘可能小的原因。 有了這些基礎的概念之後,我們開始實現我們的神經網路: -
初始化
class RNNNumpy: def __init__(self, word_dim, hidden_dim=100, bptt_truncate=4): # Assign instance variables self.word_dim = word_dim self.hidden_dim = hidden_dim self.bptt_truncate = bptt_truncate # Randomly initialize the network parameters self.U = np.random.uniform(-np.sqrt(1./word_dim), np.sqrt(1./word_dim), (hidden_dim, word_dim)) self.V = np.random.uniform(-np.sqrt(1./hidden_dim), np.sqrt(1./hidden_dim), (word_dim, hidden_dim)) self.W = np.random.uniform(-np.sqrt(1./hidden_dim), np.sqrt(1./hidden_dim), (hidden_dim, hidden_dim))這裡我們不能直接將 U,V,W 直接初始化為 0, 因為這會導致在所有的 layers 中的 semmetric calculations 的問題。我們必須隨機初始化它。因為很多研究表明,合適的初始化對訓練結果是有影響的。並且最好的初始化方法取決於我們選擇什麼樣的啟用函式,當前模型我們使用的是 tanh。[這篇論文](http://jmlr.org/proceedings/papers/v9/glorot10a/glorot10a.pdf)說一種推薦的辦法是將權重隨機初始化為在 +-1/sqrt(n) 之間的數。 -
前向傳播( predict word probabilities)
def forward_propagation(self, x): # The total number of time steps T = len(X) # During forward propagation, we save all hidden states in s because need them later # We add one additional element for the initial hidden, which we set to 0 s = np.zeros((T+1, self,hidden_dim)) s[-1] = np.zeros(self.hidden_dim) # The outputs at each time step. Again, we save them for later o = np.zeros((T, self.word_dim)) # For each time step ... for t in np.arange(T): # Note that we are indxing U by x[t]. This is the same as multiplying U with a one-hot vector. s[t] = np.tanh(self.U[:, x[t]] + self.W.dot(s[t-1])) o[t] = softmax(self.V.dot(s[t])) return [o,s] RNNNumpy.forward_propagation = forward_propagation這裡返回的 o 和 s 會在接下來被用作計算梯度,這樣可以避免重複計算。輸出 o 的每一個元素都代表單詞表中每個詞出現的概率。但在有些時候,我們僅需要概率最高的那個 word,為此我們可以做如下 **precdict**:def predict(self, x): # Perform forward propagation and return index of the highest score o, s = self.forward_propagation(x) return np.argmax(o, axis=1) RNNNumpy.predict = predict現在來看一下效果:np.random.seed(10) model = RNNNumpy(vocabulary_size) o, s = model.forward_propagation(X_train[10]) print o.shape() print o(45, 8000) [[ 0.00012408 0.0001244 0.00012603 ..., 0.00012515 0.00012488 0.00012508] [ 0.00012536 0.00012582 0.00012436 ..., 0.00012482 0.00012456 0.00012451] [ 0.00012387 0.0001252 0.00012474 ..., 0.00012559 0.00012588 0.00012551] ..., [ 0.00012414 0.00012455 0.0001252 ..., 0.00012487 0.00012494 0.0001263 ] [ 0.0001252 0.00012393 0.00012509 ..., 0.00012407 0.00012578 0.00012502] [ 0.00012472 0.0001253 0.00012487 ..., 0.00012463 0.00012536 0.00012665]]```
45 表示有對於給定的句子的 45 個word,我們的模型產出了 8000 個預測結果,分別代表下一個詞的概率。需要注意的是,因為我們是隨機初始化的 U, V, W,因此這裡產出的”預測“實際上也是隨機的結果。下面給出了概率最高的詞的索引:
python predictions = model.predict(X_train[10]) print predictions.shape print predictions
(45,) [1284 5221 7653 7430 1013 3562 7366 4860 2212 6601 7299 4556 2481 238 2539 21 6548 261 1780 2005 1810 5376 4146 477 7051 4832 4991 897 3485 21 7291 2007 6006 760 4864 2182 6569 2800 2752 6821 4437 7021 7875 6912 3575]-
計算損失
在訓練網路之前,我們首先需要定義一個衡量誤差的 metric,這就是以前常說的損失函式 loss function L。我們的目標是找到使得損失函式最小化的 U, V, W。損失函式的一種常見的選擇就是交叉熵損失。如果我們有 N 個訓練樣本(words)和 C 個類別(vocabulary_size),那麼給定了真實的label值,我們的預測 o 的損失函式是:
def calculate_total_loss(self, x, y): L = 0 # For each sentence ... for i in np.arange(len(y)): o, s = self.forward_propagation(x[i]) # We only care about our prediction of the 'correct' words correct_word_predictions = o[np.arange(len(y[i])), y[i]] # Add to the loss based on how off we are L += -1 * np.sum(np.log(correct_word_predictions)) return L def calculate_loss(self, x, y): # Divide the total loss by the number of training examples N = np.sum((len(y_i) for y_i in y)) return self.calculate_total_loss(x,y)/N RNNNumpy.calculate_total_loss = calculate_total_loss RNNNumpy.calculate_loss = calculate_loss在隨機情況下,我們的實現計算出的損失可以當做 baseline。隨機的情況也可以用於保證我們的實現是正確的。vocabulary 中有 C 個 words,所以理論上每個 word 被預測到的概率應該是 1/C,這時候我們得到的損失函式是 logC:
# Limit to 1000 examples to save time print "Expected Loss for random predictions: %f" % np.log(vocabulary_size) print "Actual loss: %f" % model.calculate_loss(X_train[:1000], y_train[:1000])Expected Loss for random predictions: 8.987197 Actual loss: 8.987440我們計算出的結果跟理論值很接近,這說明我們的實現是正確的。
-
使用 BPTT 和 SGD 訓練 RNN
再次明確一下我們的目標:
找到使得損失函式最小的 U, V, W
最常用的方式是 隨機梯度下降 Stochastic Gradient Descend。SGD的思路是很簡單的,在整個訓練樣本中迭代,每次迭代我們朝某個使得無插減小的方向 nudge 我們的引數。這些方向通過分別對 L 求 U, V, W的偏導來確定。 SGD 也需要 learning rate,它定義了每一步我們要邁多大。 SGD 也是神經網路最受歡迎的一種優化的方式,也適用於其他很多的機器學習演算法。關於如何優化 SGD 也已經有了很多的研究,比如使用 batching,parallelism 和 adaptive learning rates。儘管基本想法很簡單,將 SGD 實現地很有效率卻是一個比較複雜的事情。
關於 SGD 的更多內容,這裡有個教程.
這裡實現的是一個簡單版本的 SGD,即使沒有任何關於優化的基礎知識,也是可以看懂的。
現在問題來了,我們應該如何計算梯度呢?在傳統的神經網路中,我們使用反向傳播演算法。在 RNN 中,我們使用的是它的一個變體: Backpropagation Through Time(BPTT)。由於引數是在所有的層之間共享的,因此當前層的梯度值的計算除了要基於當前的這一步,還有依賴於之前的 time steps。這其實就是應用微積分的鏈式法則。目前我們只是寬泛地談了一下 BPTT,後面會做詳細介紹。
關於 back propagation ,這裡有兩個部落格可以參考:1, 2
目前暫時將 BPTT 看作一個黑盒,它以訓練資料(x,y)為輸入,返回損失函式在 U, V, W 上的導數值。
def bptt(self, x, y): pass RNNNumpy.bptt = bptt -
Gradient Checking
這裡提供的一條 tip 是,在你實現反向傳播演算法的時候,最好也實現一個 gradient checking,它用來驗證你的程式碼是否正確。 gradient checking 的想法是某個引數的倒數等於那一點的斜率,我們可以將引數變化一下,然後除以變化率來近似地估計:
然後我們可以比較使用 BP 計算的梯度和使用上面的公式計算的梯度。如果沒有很大的差別的話,說明我們的實現是正確的。
上面的估計需要計算每個引數的 total loss,因此 gradient checking 也是很耗時的操作,在這裡,我們只要在一個小規模的例子上模擬一下就可以了。
def gradient_check(self, x, y, h=0.001, error_threshold=0.01): # Calculate the gradients using backpropagation. We want to checker if these are correct. bptt_gradients = self.bptt(x, y) # List of all parameters we want to check. model_parameters = ['U', 'V', 'W'] # Gradient check for each parameter for pidx, pname in enumerate(model_parameters): # Get the actual parameter value from the mode, e.g. model.W parameter = operator.attrgetter(pname)(self) print "Performing gradient check for parameter %s with size %d." % (pname, np.prod(parameter.shape)) # Iterate over each element of the parameter matrix, e.g. (0,0), (0,1), ... it = np.nditer(parameter, flags=['multi_index'], op_flags=['readwrite']) while not it.finished: ix = it.multi_index # Save the original value so we can reset it later original_value = parameter[ix] # Estimate the gradient using (f(x+h) - f(x-h))/(2*h) parameter[ix] = original_value + h gradplus = self.calculate_total_loss([x],[y]) parameter[ix] = original_value - h gradminus = self.calculate_total_loss([x],[y]) estimated_gradient = (gradplus - gradminus)/(2*h) # Reset parameter to original value parameter[ix] = original_value # The gradient for this parameter calculated using backpropagation backprop_gradient = bptt_gradients[pidx][ix] # calculate The relative error: (|x - y|/(|x| + |y|)) relative_error = np.abs(backprop_gradient - estimated_gradient)/(np.abs(backprop_gradient) + np.abs(estimated_gradient)) # If the error is to large fail the gradient check if relative_error > error_threshold: print "Gradient Check ERROR: parameter=%s ix=%s" % (pname, ix) print "+h Loss: %f" % gradplus print "-h Loss: %f" % gradminus print "Estimated_gradient: %f" % estimated_gradient print "Backpropagation gradient: %f" % backprop_gradient print "Relative Error: %f" % relative_error return it.iternext() print "Gradient check for parameter %s passed." % (pname) RNNNumpy.gradient_check = gradient_check # To avoid performing millions of expensive calculations we use a smaller vocabulary size for checking. grad_check_vocab_size = 100 np.random.seed(10) model = RNNNumpy(grad_check_vocab_size, 10, bptt_truncate=1000) model.gradient_check([0,1,2,3], [1,2,3,4]) -
SGD 實現
現在我們已經可以為引數計算梯度了:
- sgd_step 用來計算梯度值和進行批量更新
- 一個在訓練集上迭代的外部迴圈,並且不斷調整 learning rate
# Performs one step of SGD def numpy_sdg_step(self, x, y, learning_rate): # Calculate the gradients: dLdU, dLdV, dLdW = self.bptt(x,y) # Change parameters according to gradients and learning rate self.U -= learning_rate * dLdU self.V -= learning_rate * dLdV self.W -= learning_rate * dLdW RNNNumpy.sgd_step = numpy_sdg_step# Outer SGD loop # - model: The RNN model instance # - X_train: The training dataset # - y_train: The training data labels # - learning_rate: Initial learning rate for SGD # - nepoch: Number of times to iterate through the complete dataset # - evaluate_loss_after: Evaluate the loss after this many epochs def train_with_sgd(model, X_train, y_train, learning_rate=0.005, nepoch=100, evaluate_loss_after=5): losses = [] num_examples_seen = 0 for epoch in range(nepoch): # Optionally evaluate the loss if (epoch % evaluate_loss_after == 0): loss = model.calculate_loss(X_train, y_train) losses.append(num_examples_seen, loss)) time = datetime.now().strftime('%Y-%n-%d %H:%M:%S') print '%s: Loss after num_examples_seen=%d epoch=%d' %(time, num_examples_seen, epoch, loss) # Adjust the learning rate if loss increases if(len(losses) >: 1 and losses[-1][1] > losses[-2][1]): learning_rate = learning_rate * 0.5 print 'Setting learning rate to %f' % learning_rate sys.stdout.flush() # For each training example ... for i in range(len(y_train)): # One SGD step model.sgd_step(X_train[i], y_train[i], learning_rate) num_examples_seen += 1到這裡,已經基本完成了。先試一下:
np.random.seed(10) model = RNNNumpy(vocabulary_size) %timeit model.sgd_step(X_train[10], y_train[10], 0.005)你會發現速度真的很慢,因此我們需要加速我們的程式碼:
例如,使用 hierarchical softmax 或者加一個 projection layer 來避免大矩陣的乘法操作(這裡和這裡)
這裡並沒有採用上面提到的優化方式,因為我們還有一個選擇,在 GPU 上跑我們的 model。在那之前,去哦們現在一個小資料集上測試一下 loss 是不是下降的:
np.random.seed(10) # Train on a small subset of the data to see what happens model = RNNNumpy(vocabulary_size) losses = train_with_sgd(model, X_train[:100], y_train[:100], nepoch=10, evaluate_loss_after=1)2015-09-30 10:08:19: Loss after num_examples_seen=0 epoch=0: 8.987425 2015-09-30 10:08:35: Loss after num_examples_seen=100 epoch=1: 8.976270 2015-09-30 10:08:50: Loss after num_examples_seen=200 epoch=2: 8.960212 2015-09-30 10:09:06: Loss after num_examples_seen=300 epoch=3: 8.930430 2015-09-30 10:09:22: Loss after num_examples_seen=400 epoch=4: 8.862264 2015-09-30 10:09:38: Loss after num_examples_seen=500 epoch=5: 6.913570 2015-09-30 10:09:53: Loss after num_examples_seen=600 epoch=6: 6.302493 2015-09-30 10:10:07: Loss after num_examples_seen=700 epoch=7: 6.014995 2015-09-30 10:10:24: Loss after num_examples_seen=800 epoch=8: 5.833877 2015-09-30 10:10:39: Loss after num_examples_seen=900 epoch=9: 5.710718我麼可以看到, loss 的確是在一直下降的。
-
使用 Theano 在 GPU 上訓練我們的網路
這裡有一個 Theano 的[教程](tutorial。
重新寫了一個RNNTheano,將 numpy 的計算使用 Theano 中的計算進行了替代。
np.random.seed(10) model = RNNTheano(vocabulary_size) %timeit model.sgd_step(X_train[10], y_train[10], 0.005) -
生成文字
現在已經得到了模型,我們可以用來生成文字了:
def generate_sentence(model): # We start the sentence with the start token new_sentence = [word_to_index[sentence_start_token]] # Repeat until we get an end token while not new_sentence[-1] == word_to_index[sentence_end_token]: next_word_probs = model.forward_propagation(new_sentence) sampled_word = word_to_index[unknown_token] # We don't want to sample unknown words while sampled_word == word_to_index[unknown_token]: samples = np.random.multinomial(1, next_word_probs[-1]) sampled_word = np.argmax(samples) new_sentence.append(sampled_word) sentence_str = [index_to_word[x] for x in new_sentence[1:-1]] return sentence_str num_sentences = 10 senten_min_length = 7 for i in range(num_sentences): sent = [] # We want long sentences, not sentences with one or two words while len(sent) < senten_min_length: sent = generate_sentence(model) print " ".join(sent)下面是測試效果:
Anyway, to the city scene you’re an idiot teenager. What ? ! ! ! ! ignore! Screw fitness, you’re saying: https Thanks for the advice to keep my thoughts around girls. Yep, please disappear with the terrible generation.
-
現在的模型存在的問題是
vanilla RNN 幾乎不能成成有意義的文字,因為它不能學習隔了很多步的依賴關係。
接下來我們先深入瞭解一下 BPTT 和 vanishing gradient,然後開始介紹 LSTM。
在這一部分,主要了解一下 BPTT 以及它跟傳統的反向傳播演算法有什麼區別。然後嘗試理解 vanishing gradient 的問題,這個問題也催生出了後來的 LSTMs 和 GRUs,後兩者也是當今 NLP 領域最有效的模型之一。
起初,vanishing gradient 問題是在 1991 年被 Sepp Hochreiter 首次發現的,並且在最近由於深層架構的使用而越來越受關注。
這一部分需要偏導以及基本的反向傳播理論的基礎,如果你並不熟悉的話,可以看這裡,這裡和這裡。
-
BPTT
上式為我們如何計算總的交叉熵損失。
我們將每句話 sentence 看做一個 training example,因此整體的損失就是每一步的損失的和
再次明確,我們的目標是計算出損失函式對 U, V, W 的梯度,然後使用梯度下降演算法來學習更好的引數。類似於我們將誤差相加,我們也將每個訓練樣本在每一步的梯度相加:
為了計算這些梯度值,我們使用求到的鏈式法則。這就是所謂的反向傳播演算法,它使誤差從後向前傳播。比如,我們以 E3 為例:
由於,所以我們需要繼續向前求導:
從上面這個式子我們可以看出,由於 W 是在每一步共享的,我們在 t=3 的時候需要一直反向傳播到 t=0 time step:
這其實跟我們在深度前向反饋神經網路中用的標準的反向傳播演算法是相通的,不同的地方在於對於 W 我們將每一步求和。在傳統的 NN 中我們並沒有在層間共享權值,因此我們也就不需要求和這一步。
def bptt(self, x, y): def bptt(self, x, y): T = len(y) # Perform forward propagation o, s = self.forward_propagation(x) # We accumulate the gradients in these variables dLdU = np.zeros(self.U.shape) dLdV = np.zeros(self.V.shape) dLdW = np.zeros(self.W.shape) delta_o = o delta_o[np.arange(len(y)), y] -= 1. # For each output backwards ... for t in np.arange(T)[::-1]: dLdV += np.outer(delta_o[t], s[t].T) delta_t = self.V.T.dot(delta_o[t])*(1-(s[t]**2)) # Back Propagation Through Time (for at most self.bptt_truncate steps) for bptt_step in np.arange(max(0,t-self.bptt_truncate), t+1)[::-1]: # print "Backpropagation step t=%d bptt step=%d" %(t, bptt_step) dLdW += np.outer(delta_t, s[bptt_step-1]) dLdU[:,x[bptt_step]] += delta_t # Update delta for next step delta_t = self.W.T.dot(delta_t) * (1 - s[bptt_step-1] ** 2) return [dLdU, dLdV, dLdW]看到這裡你應該也能體會到為什麼標準的 RNNs 很難訓練了,sequence 可能會相當長,因此你需要法相傳播很多層,在實際中,很多人會選擇將反向傳播 truncate 為 a few steps。
-
the Vanishing Gradient Problem
讓我們再看一下這個公式:
其中,是一個鏈式法則,例如,
值得注意的是,因為我們是在對一個 vector function 關於一個 vector 求導,結果其實就是一個矩陣,這個矩陣叫做 雅克比矩陣(Jacobian Matrix),其中每個元素都是逐點的求導:
上面的 Jacobian Matrix 的第二正規化的上界是 1,這是很符合直覺的,因為我們使用的 tanh(雙曲正切)啟用函式將所有的值對映到 0-1 之間,它的導數也被限定在 1 內。下圖是 tanh 和它的導數:
我們可以看到, tanh 的導數在兩端均為 0。他們都接近一條直線。當這種情況發生時,我們說對應的神經元已經 saturate 了。它們的梯度值為 0,並且在 drive 之前層的其他梯度值也朝 0 發展。因此,矩陣中有 small values 的多個矩陣乘法會使得梯度值以指數級的速度 shrinking。最終,在幾步之後,梯度就會徹底消失掉。這時,來自很遠的地方的梯度貢獻變成了 0,這些步也就沒有了貢獻。因此,你最終還是無法學習長距離依賴。Vanishing Gradient 並不只在 RNNs 中存在,它們在 deep Feedforward Neural Networks 中也存在,只是 RNNs 一般傾向於生成更深層次的神經網路,也就使得這個問題在 RNNs 中尤其明顯。
類比一下,如果矩陣中的值變得很大那麼神經網路的引數會開始 ”exploging“, 而不是 ”vanishing“。因此,我們將這類問題稱作 ”exploding/vanishing gradient problem“。
實際中人們更長接觸到的是 vanishing problem,這有兩個原因:
- exploding gradient 一般是很明顯的,因為到某一步時,這些引數值會變成 NaN,你的程式也會 crash 掉。
- 在到達一個閾值時截斷 clip 梯度可以比較好的解決 exploding 的問題,但是 vanishing 就沒這麼容易解決了,因為它表現得不如 exploding 明顯。
幸運的是,現在已經有一些可行的操作來應對 vanishing gradient 的問題。
例如,對 W 進行更加合適的初始化操作會 alleviate 這個問題。
人們更傾向於採用 ReLU 來替代 tanh 或者 sigmoid 來作為啟用函式使用。ReLU 的導數是一個常數,要麼為 0,要麼為 1。所以它可以比較好地規避 vanishing 的問題。
更加進階的方法就是使用 LSTMs 或者 GRU 了
LSTMs 最早在 1997 年被提出,它可能是目前為止 NLP 領域應用最廣泛的模型。
GRUs 第一次提出是在 2014 年,它是一個簡化版本的 LSTMs。
以上兩種 RNN 結構都是用來顯式地被設計為解決 vanishing gradient 問題,現在讓我們正式開始:
在完整的瞭解 RNNs 的細節之前,我已經學習過了 LSTMs,詳情見我的這篇 深入理解LSTM。
概括來說,LSTMs 針對 RNNs 的 long-term dependencies 問題,引入了 門機制 gating 來解決這個問題。先來回顧一下上面我這篇 post 中提到的 LSTMs 的主要的計算公式:
其中,o 表示逐點操作。
i, f, o 分別是 輸入、遺忘和輸出門。從上面我們一刻看到他們的公式是相同的,只不過對應的引數矩陣不同。關於input, forget 和 output 分別代表什麼意義,看上面這篇 post。需要注意的一點是,所有這些 gates 有相同的維度 d,d 就是 hidden state size。比如,前面的 RNNs 實現中的 hidden_size = 100。
g 是基於當前輸入和前一步隱狀態的 hidden state。這跟前面的 vanilla RNNs 是一樣求的。只是將 U,W 的名字改了一下。但是,我們沒有像在 RNN 中那樣將 g 當做 new hidden state,而是用前面的 input gate 挑選出其中一些來。
c_t 是當前 unit 的 ’memory‘。從上面的公式可以看出,它定義了我們怎樣將之前的記憶和和新的輸入結合在一起。給定了 c_t,我們就可以計算出 hidden_state s_t,使用上面的公式。
不知你是否已經感覺到, plain/vanilla RNNs 可以看做是 LSTMs 的一個特殊變體,你把 input gate 固定位 1,forget gate 固定位 0, output gate 固定位 1,你就幾乎得到了一個標準的 RNN。唯一不同的地方是多了個 tanh。
綜上,門機制使得 LSTMs 可以顯式地解決長距離依賴的問題。通過學習門的引數,網路就知道了如何處理它的 memory。
現在已經有了很多 LSTMs 的變體,比如一種叫做 peephole 的變體:
-
GRUs
GRU(Gated Recurrent Unit) 有兩個 gate, 一個 reset gate r, 一個 update gate z。顧名思義,reset gate 決定如何組合新的輸入和之前的記憶,update gate 決定多少之前的記憶被保留。如果將 reset gate 置為全 1,將 update gate 置為全 0,就得到了 vanilla RNNs。
GRU 和 LSTM 的區別主要在於:
- GRU 只有兩個 gates。
- GRU 沒有 internal memory(c_t),沒有 output gate
- GRU 的 input 和 forget 耦合在一起,形成 update gate。reset gate 直接被作用在 previous hidden state 上。因此,reset gate 實際上在 LSTM 中被分在了 r 和 z 中。
- GRU 在計算輸出時,不再使用另外的非線性函式處理。
-
例項: LSTM Networks for Sentiment Analysis
這個例項來自於 Theano 的官方文件,使用 IMDB dataset 來做情感分析。
具體來說,給定一篇影評,預測出評價是積極的還是消極的,這是一個二分類問題。
LSTM model introduces a new structure called a memory cell (see below). A memory cell is composed of four main elements:
- an input gate
- a neuron with a self-recurrent connection (a connection to itself)
- a forget gate
- an output gate
The self-recurrent connection has a weight of 1.0 and ensures that, barring any outside interference, the state of a memory cell can remain constant from one timestep to another.
The gates serve to modulate the interactions between the memory cell itself and its environment.
- The input gate can allow incoming signal to alter the state of the memory cell or block it.
- On the other hand, the output gate can allow the state of the memory cell to have an effect on other neurons or prevent it.
- Finally, the forget gate can modulate the memory cell’s self-recurrent connection, allowing the cell to
