最近又複習了下最大流問題，每次看這部分的內容都會有新的收穫。可以說最大流問題的資料網上一搜一大把，根本沒有必要自己寫；但是大部分資料上的專業術語太多了，初學很難理解，至少我當年學這部分的時候前幾次就沒有看懂。所以我準備備份一點個人的理解。

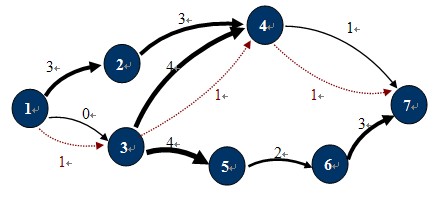圖-1

  如圖-1所示，在這個運輸網路中，源點S和匯點T分別是1,7，各邊的容量為C(u,v)。圖中紅色虛線所示就是一個可行流。標準圖示法如圖-2所示：

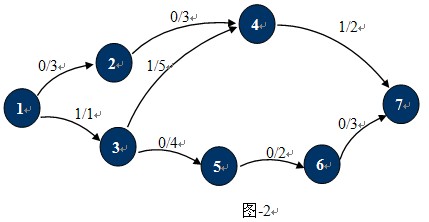
其中p(u,v) / c(u,v)分別表示該邊的實際流量與最大容量。

 

關於最大流

  熟悉了什麼是網路流，最大流也就很好理解了。就是對於任意的u∈V-{s},使得p(s,u)的和達到最大。上面的運輸網路中，最大流如圖-3所示：MaxFlow=p(1,2)+p(1,3)=2+1=3。

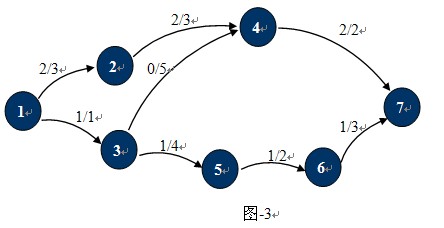
  在介紹最大流問題之前，先介紹幾個概念：殘餘網路，增廣路徑，反向弧，最大流定理以及求最大流的Ford-Fulkerson方法。

殘餘網路 增廣路徑 反向弧

  觀察下圖-4，這種狀態下它的殘餘網路如圖-5所示：

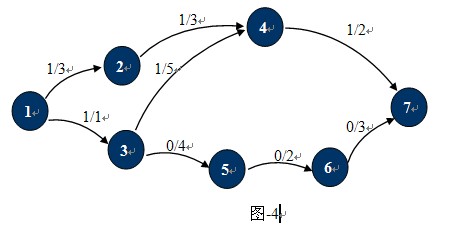
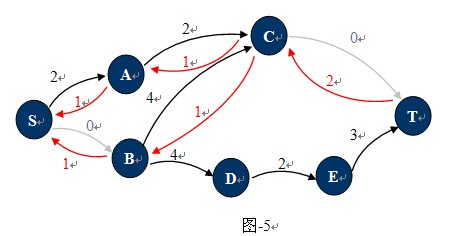
  也許現在你已經知道什麼是殘餘網路了，對於已經找到一條從S 到T的路徑的網路中，只要在這條路徑上，把C(u,v)的值更新為C(u,v)-P(u,v)，並且新增反向弧C(v,u)。對應的增廣路徑Path為殘留網路上從S到T的一條簡單路徑。圖-4中1，2，4，7就是一條增廣路徑，當然還有1，3，4，7。

  此外在未做任何操作之前，原始的有向圖也是一個殘餘網路，它僅僅是未做任何更新而已。

 

最大流定理

  如果殘留網路上找不到增廣路徑，則當前流為最大流；反之，如果當前流不為最大流，則一定有增廣路徑。

 

Ford-Fulkerson方法

  介紹完上面的概念之後，便可以用Ford-Fulkerson方法求最大流了。為什麼叫Ford-Fulkerson方法而不是演算法，原因在於可以用多種方式實現這一方法，方式並不唯一。下面介紹一種基於廣度優先搜尋(BFS)來計算增廣路徑P的演算法：Edmonds-Karp演算法。

  演算法流程如下：

  設佇列Q：儲存當前未訪問的節點，隊首節點出隊後，成為已檢查的標點；

  Path陣列：儲存當前已訪問過的節點的增廣路徑；

  Flow陣列：儲存一次BFS遍歷之後流的可改進量；

  Repeat:

    Path清空；

    源點S進入Path和Q，Path[S]<-0，Flow[S]<-+∞；

    While Q非空 and 匯點T未訪問 do

        Begin

            隊首頂點u出對；

            For每一條從u出發的弧(u,v) do

                If v未訪問 and 弧(u,v) 的流量可改進；

                Then Flow[v]<-min(Flow[u],c[u][v]) and v入隊 and Path[v]<-u；

    End while

    If(匯點T已訪問)

    Then 從匯點T沿著Path構造殘餘網路；

  Until 匯點T未被訪問

 

應用例項

  這是一道最大流的入門題，題目如下：

Description

  Every time it rains on Farmer John's fields, a pond forms over Bessie's favorite clover patch. This means that the clover is covered by water for awhile and takes quite a long time to regrow. Thus, Farmer John has built a set of drainage ditches so that Bessie's clover patch is never covered in water. Instead, the water is drained to a nearby stream. Being an ace engineer, Farmer John has also installed regulators at the beginning of each ditch, so he can control at what rate water flows into that ditch. 
Farmer John knows not only how many gallons of water each ditch can transport per minute but also the exact layout of the ditches, which feed out of the pond and into each other and stream in a potentially complex network. 
Given all this information, determine the maximum rate at which water can be transported out of the pond and into the stream. For any given ditch, water flows in only one direction, but there might be a way that water can flow in a circle.

Input

  The input includes several cases. For each case, the first line contains two space-separated integers, N (0 <= N <= 200) and M (2 <= M <= 200). N is the number of ditches that Farmer John has dug. M is the number of intersections points for those ditches. Intersection 1 is the pond. Intersection point M is the stream. Each of the following N lines contains three integers, Si, Ei, and Ci. Si and Ei (1 <= Si, Ei <= M) designate the intersections between which this ditch flows. Water will flow through this ditch from Si to Ei. Ci (0 <= Ci <= 10,000,000) is the maximum rate at which water will flow through the ditch.

Output

  For each case, output a single integer, the maximum rate at which water may emptied from the pond.

Sample Input

5 4

1 2 40

1 4 20

2 4 20

2 3 30

3 4 10

Sample Output

50

 1 #include <iostream>
 2 #include <queue>
 3 using namespace std;
 4 
 5 const int N = 210;
 6 const int INF = 0x7FFFFFFF;
 7 int n,m,map[N][N],path[N],flow[N],start,end;
 8 queue<int> q;
 9 
10 int bfs(){
11     int i,t;
12     while(!q.empty()) q.pop();
13     memset(path,-1,sizeof(path));
14     path[start]=0,flow[start]=INF;
15     q.push(start);
16     while(!q.empty()){
17         t=q.front();
18         q.pop();
19         if(t==end) break;
20         for(i=1;i<=m;i++){
21             if(i!=start && path[i]==-1 && map[t][i]){
22                 flow[i]=flow[t]<map[t][i]?flow[t]:map[t][i];
23                 q.push(i);
24                 path[i]=t;
25             }
26         }
27     }
28     if(path[end]==-1) return -1;
29     return flow[m];                   //一次遍歷之後的流量增量30 }
31 int Edmonds_Karp(){
32     int max_flow=0,step,now,pre;
33     while((step=bfs())!=-1){          //找不到增路徑時退出34         max_flow+=step;
35         now=end;
36         while(now!=start){
37             pre=path[now];
38             map[pre][now]-=step;      //更新正向邊的實際容量39             map[now][pre]+=step;      //新增反向邊40             now=pre;
41         }
42     }
43     return max_flow;
44 }
45 int main(){
46     int i,u,v,cost;
47     while(scanf("%d %d",&n,&m)!=EOF){
48         memset(map,0,sizeof(map));
49         for(i=0;i<n;i++){
50             scanf("%d %d %d",&u,&v,&cost);
51             map[u][v]+=cost;           //not just only one input52         }
53         start=1,end=m;
54         printf("%d\n",Edmonds_Karp());
55     }
56     return 0;
57 }
58