1.1 描述

高精度演算法，屬於處理大數字的數學計算方法。在一般的科學計算中，會經常算到小數點後幾百位或者更多，當然也可能是幾千億幾百億的大數字。一般這類數字我們統稱為高精度數，高精度演算法是用計算機對於超大資料的一種模擬加，減，乘，除，乘方，階乘，開方等運算。對於非常龐大的數字無法在計算機中正常儲存，於是，將這個數字拆開，拆成一位一位的，或者是四位四位的儲存到一個數組中， 用一個數組去表示一個數字，這樣這個數字就被稱為是高精度數。高精度演算法就是能處理高精度數各種運算的演算法，但又因其特殊性，故從普通數的演算法中分離，自成一家。

對於這類問題，不要指望int double這些東西了，基本資料型別不可能存的下。我們可以把這兩個數當成字串輸入到陣列中，然後模擬手動的豎式運算（不會的話，回去上小學）得出結果。

說白了，高精度計算就是解決long long也解決不了的問題。

1.2 分析與處理資料

1.2.1 當要處理的資料很長時，我們可以採用字串的方式輸入，這樣可以輸入很長的數，利用字串函式和操作運算，將每一位數取出，存入一個數組裡。

//1.2.1 資料的接收和儲存方法 
void input()
{
	string s;
	cin>>s;//讀入字串
	a[0]=s.length();//取s字串的長度，並存入a[0]中
	for(i=1;i<=a[0];i++)
	{
		a[i]=s[a[0]-i]-'0';//將字串s轉化為數字存入a陣列中，並倒敘儲存 
		//為什麼要倒敘？為了給進位留足空間
		//高精度的儲存是把每一位單獨儲存，且是倒序儲存，陣列a[1]是這個數的個位，a[2]是這個數的十位，以此類推
	}
}
 

1.2.2 接收時使用字串，所以它的位數等於字串的長度。

1.2.3 當兩個運算元長度不一樣時，需要進行補零。

//1.2.3 補零問題
void NumFill()
{
	string s1,s2;
	int len1,len2,i;
	cin>>s1>>s2;//讀入字串
	len1=s1.length();//求字串1長度 
	len2=s2.length();//求字串2長度
	if(len1<len2)//如果字串1長度小於字串2長度 
	{//對字串1補零 
		for(i=1;i<=len2-len1;i++)//len2-len1就是需要補零的長度 
		{
			s1='0'+s1;
		}
	}
	else//否則字串1長度大於字串2長度 
	{//對字串2補零 
		for(i=1;i<=len1-len2;i++)//len1-len2就是需要補零的長度 
		{
			s2='0'+s2;
		}
	}
} 
 

1.2.4 進位與借位

//1.2.4 進位處理
void plus()//加法進位 
{
	c[i]=a[i]+b[i];//虛擬碼，c[i]來儲存高精度數，a[i]和b[i]是被分離的2個加數。
	if(c[i]>=10)//如果a[i]+b[i]大於0了，很顯然，要進位。不知道的給我重讀1年級數學
	{
		c[i]=c[i]%10;//把得到的結果分離出來
		++c[i+1];//那麼後一位進一 
	} 
}
void minus()//減法借位 
{
	if(a[i]<b[i])//先判斷被減數是否小於減數 
	{
		--a[i+1];//後一位借位，所以減1 
		a[i]+=10;//那麼當前加10 
	}
	c[i]=a[i]-b[i];//這個時候算差 
}
void multiplication()//乘法進位 
{
	c[i+j-1] = a[i]*b[i]+x+c[i+j-1];//x表示的是進位數
	//我們再宣告一個數組c來儲存答案。大家通過一個簡單的乘法運算進行模擬就可以看出。 
	//結果 = 當前乘積a[i]*b[i] + 進位數x + 原數 
	x=c[i+j-1]/10;//需要的進位數 
	c[i+j-1]%=10;//取下一位數
	//這裡應該有for迴圈的 
}

1.3 高精度計算演算法和思想

1.3.1 高精度加法

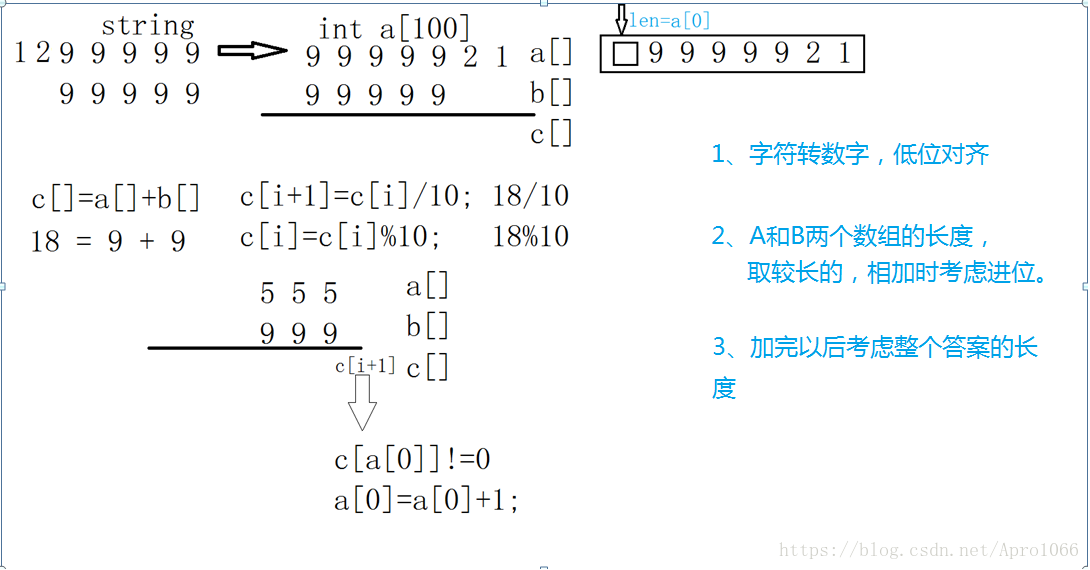
在讀小學時，我們做加法都採用豎式方法，利用豎式，我們可以寫出兩個整數相加的高精度演算法。

那麼，要想求出高精度資料，就需要一定的步驟演算法。

1.字元轉數字，且低位對齊；

2.a、b兩個陣列的長度，取較長的。相加時，考慮進位；

3.考慮得數的長度和0位；

4.逆序輸出。

Ps:其實低位對齊和逆序，只是方便計算和順應演算法思想罷了，不必要去思考為什麼要這樣做。

//1.3.1 高精度加法 
#include <cstdio>
#include <iostream>
#include <cstring>
#define r(i,a,b) for(i=a;i<=b;i++)//為了省事而已 
using namespace std;
int main()
{
	char a1[101]={},b1[101]={}; 
	int a[101]={},b[101]={},c[101]={},lena,lenb,lenc,i,x;
	gets(a1);
	gets(b1);
	lena=strlen(a1);//取長度 
	lenb=strlen(b1);//取長度 
	r(i,0,lena-1)//從0到陣列長度-1正好把資料讀完 
	{
		a[lena-i]=a1[i]-48;//字元轉數字 
	}
	r(i,0,lenb-1)//從0到陣列長度-1正好把資料讀完 
	{
		b[lenb-i]=b1[i]-48;//字元轉數字 
	}
	lenc=1;//用來處理陣列長度 
	x=0;//用來計算進位 
	while(lenc<=lena || lenc<=lenb)//開始計算，演算法核心 
	{
		c[lenc]=a[lenc]+b[lenc]+x;//得到的結果，應該是a[]+b[]，當然還要加上進位 
		x=c[lenc]/10;//其實不用寫if，如果此答案低於10得到的進位還是0，超過10就是1 
		c[lenc]%=10;//此答案取後一位，如果只有1位數，還是本身 
		lenc++;//繼續判斷下一位 
	}
	if(x==0)//如果最後一位可以進位 
		lenc--;
	for(i=lenc;i>=1;i--)//逆序輸出 
		cout<<c[i];
	cout<<endl;
	return 0;
}

1.3.2 高精度減法

類似加法，可以用豎式求減法。在做減法運算時，需要注意的是：被減數必須比減數大，同時需要處理錯位以及前導0。

步驟和演算法設計

1.字元轉數字，且低位對齊；

2.取a,b2個數組長度更長的那個，注意可能會有負號；

3.計算時可能會有進位；

4.高位是否存在；

5.逆序輸出。

//1.3.2 高精度減法 
#include <cstdio>
#include <cstring>
#include <iostream>
#define r(i,a,b) for(i=a;i<=b;i++)
using namespace std;
int a[257],b[257],c[257],lena,lenb,lenc,i;
char n[257],n1[257],n2[257];
int main()
{
	cin>>n1>>n2;
	if(strlen(n1)<strlen(n2) || (strlen(n1)==strlen(n2) && strcmp(n1,n2)<0))//如果被減數小於減數，值為負，兩者交換
	{
		strcpy(n,n1);
		strcpy(n1,n2);
		strcpy(n2,n);//字元交換 
		cout<<'-';//先輸出負號 
	}
	lena=strlen(n1);
	lenb=strlen(n2);
	r(i,0,lena-1)//被減數存入陣列a
	{
		a[lena-i]=int(n1[i]-'0');//字元轉數字 
	}
	r(i,0,lenb-1)//減數存入陣列a
	{
		b[lenb-i]=int(n2[i]-'0');//字元轉數字 
	}
	i=1;//控制當前陣列下標
	while(i<=lena || i<=lenb)//開始計算，核心演算法 
	{
		if(a[i]<b[i])//如果被減數比減數小，要借位 
		{
			a[i]=a[i]+10;
			a[i+1]--;
		}
		c[i]=a[i]-b[i];//因為判斷是否借位了，直接減即可 
		i++;
	}
	lenc=i;
	while((c[lenc]==0)&&(lenc>1))//判斷高位是否為0，最高位0不輸出 
		lenc--;
	for(i=lenc;i>=1;i--)//逆序輸出 
		cout<<c[i];
	cout<<endl;
	return 0;
}

1.3.3 高精度乘法

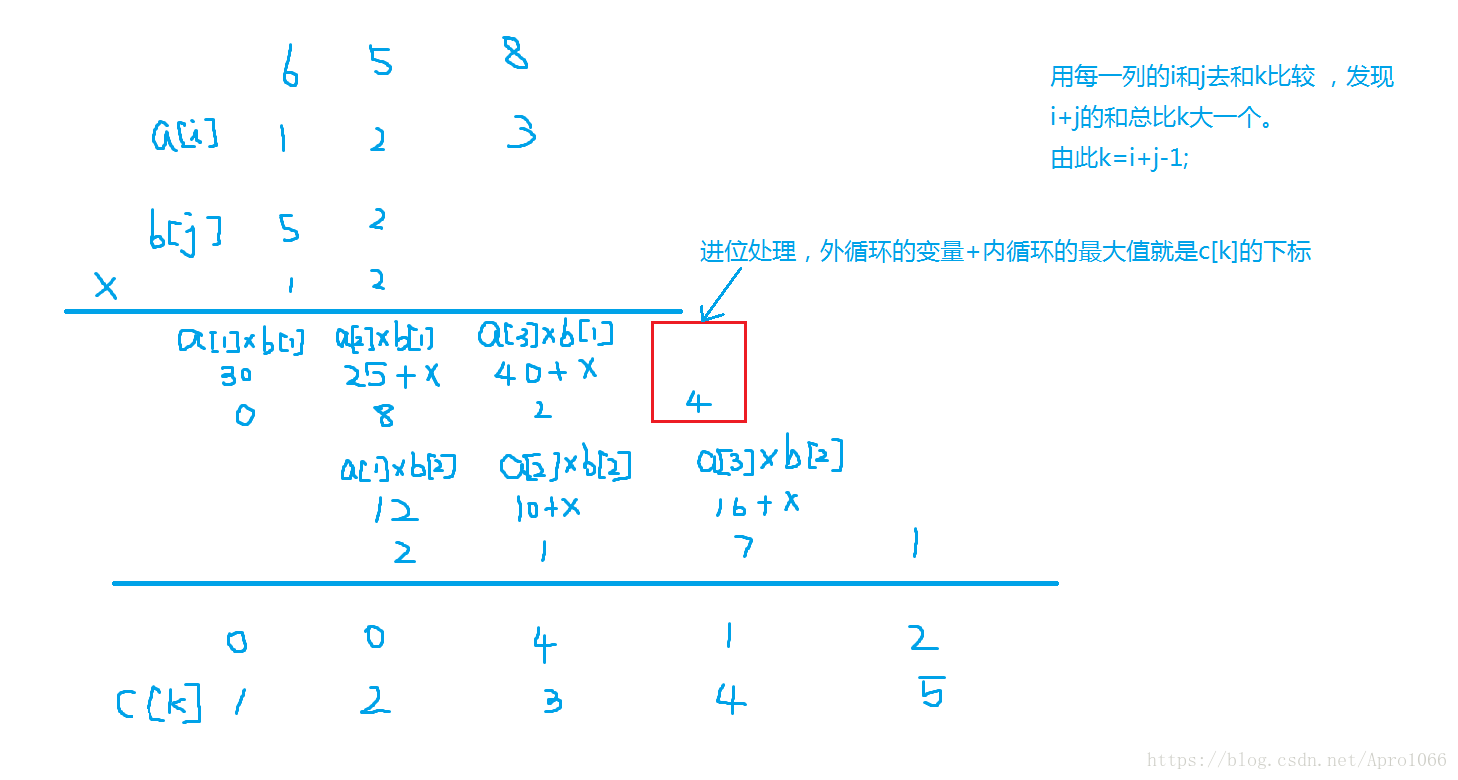
類似加法，用豎式求乘法。在做乘法運算時，同樣有進位，同時對每一位進行乘法運算時，必須進行錯位相加。

//1.3.3 高精度乘法 
#include <cstdio>
#include <cstring>
#include <iostream>
#define r(i,a,b) for(i=a;i<=b;i++)
using namespace std;
int a[257],b[257],c[257],lena,lenb,lenc,i,j,x;
char a1[257],b1[257];
int main()
{
	cin>>a1>>b1;
	lena=strlen(a1);
	lenb=strlen(b1);
	r(i,0,lena-1)
	{
		a[lena-i]=int(a1[i]-'0');
	}
	r(i,0,lenb-1)
	{
		b[lenb-i]=int(b1[i]-'0');
	}
	r(i,1,lena)
	{
		x=0;//存放進位
		r(j,1,lenb)//對乘數的每一位都處理 
		{
			c[i+j-1]=a[i]*b[j]+x+c[i+j-1];//結果 = 當前乘積a[i]*b[i] + 進位數x + 原數 
			x=c[i+j-1]/10;
			c[i+j-1]%=10;
		}
		c[i+lenb]=x;//是否需要進位 
	}
	lenc=lena+lenb;//根據乘法的原理計算計算最大長度
	//99*99，最大長度是4
	//11*10，最大長度是3 
	while(c[lenc]==0 && lenc>1)//刪除前導0 
	{
		lenc--;
	}
	for(i=lenc;i>=1;i--)
	cout<<c[i];
	cout<<endl;
	return 0;
}

1.3.4 高精度除法，高精除以低精

做除法時，每一次的商的值都在0~9，每次求得的餘數連線以後的若干位得到新的被除數，繼續做除法。因此在做高精度除法時，要涉及到乘法運算和減法運算以及移位處理。

為程式簡潔，可以避免高精度乘法，用0~9次迴圈減法取代得到商的值，對於高精度數除以低精度數，我們採用按位相除法。

//1.3.4 高精度除法，高精除以低精 
#include <cstdio>
#include <cstring>
#include <iostream>
#define r(i,a,b) for(i=a;i<=b;i++)
using namespace std;
int b,a[257],c[257],lena,lenc,i,j,x=0;//x是餘數 
char a1[257],c1[257];
int main()
{
	cin>>a1>>b;//注意，此時高精除以低精 
	lena=strlen(a1); 
	r(i,0,lena-1)
	{
		a[i+1]=a1[i]-'0';
	}
	r(i,1,lena)//模擬除法豎式，按位相除 
	{
		c[i]=(x*10+a[i])/b;
		x=(x*10+a[i])%b;
	}
	lenc=1;
	while(c[lenc]==0&&lenc<lena)//刪除前導0 
	lenc++;
	for(i=lenc;i<=lena;i++)
	cout<<c[i];
	cout<<endl;
	return 0;
}

本來還有個1.3.5的，高精數除以高精數，A.pro智力有限還沒想好..

2.1 C++ 大整數類模版--<2018.08.19更新>