堆排序詳解——java版

         近期一直再看別人的原始碼，無意中發現了他裡面使用了堆排序演算法，由於以前對於堆的排序問題都只是聽過，而沒有真正的理解過它和實踐過它。於是也借本次機會了解了一下堆排序的演算法。其實堆的排序是通過二叉樹的形式對元素進行排序，它的規律是：k_i>=k_2i並且k_i>=k_2i+1或者是k_i<=k_2i並且k_i<=k_2i+1，意思就是它的父節點一定大於（小於）它的兩個孩子們他們節點，也可以叫大堆排序（小堆排序）下面給出它們的儲存結構圖：

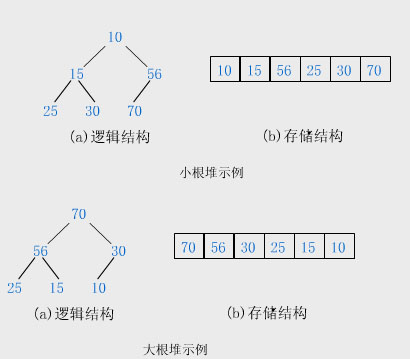
       上面的圖是我從百度百科裡面截過來的。堆排序是通過陣列的形式儲存二叉樹的資訊，那麼它就需要計算一個節點的父節點位置，和一個節點的左孩子和右孩子節點的位置，其公式分別為：父=(（i+1）/2)-1 左=(2*（i+1）)-1 右=2*（i+1）。可以通過以上幾個公式計算節點的父節點和孩子節點儲存在陣列是的位置。所以當向堆中新增元素的時候，將堆的大小新增1，用於儲存新新增進來的元素，新增元素的初始儲存位置是堆尾（注意此時還未將元素新增到堆中，只是表示在當前堆大小加一的位置將要存放新新增進來的元素）。先找到插入元素存放的位置，也就是將插入的元素和當前堆中最後元素的父節點進行比較，如果比該父節點好，則將父節點移動到移動到插入元素初始儲存的位置，而新新增元素此時的儲存位置是剛才父節點的儲存位置，將繼續和父節點的父節點進行比較，重複上面的操作，就是調換新新增的儲存位置和當前比較的父節點的位置，直到遇到一個父節點比它好或者是到了堆的頂部則停止尋找。這樣會導致一個為題，就是假設新新增的元素不是插在堆的尾部，那麼將會導致在插入新元素之後的元素就失去了堆排序的特性，就是父節點比孩子節點大（小），所以此時將還要使用一個heapify（i），方法來進行對插入新元素位置以後的元素進行重新進行堆排序。詳細的思路可見程式碼。以下貼上處我用java實現的堆排序程式碼：

public class HeapSort {

	private IntArray vertexts;//該陣列是儲存元素資訊
	private FloatArray weight;//儲存元素的權重，注意元素的位置和其對應的權重位置要一一對應
	private IntIntHashMap vertMap;//這個記錄元素儲存的位置
	private boolean Comparemode;//標記比較方式
	private float maxWeight;//最大的值

	/*public static void main(String[] args) {
		HeapSort sort = new HeapSort(true, Float.MAX_VALUE);
		for (int i = 0; i < 100; i++) {
			sort.addElement(i, (float) Math.random());
		}
		for (int i = 0; i < 100; i++) {
			System.out.print("cost :" + sort.getBestCost() + "-->");
			System.out.println(" Node: " + sort.removeBestElemment());
		}
	}*/
/**
 * 
 * @param Comparemode 該引數設定該推排序是取大的還是小的，當為true時，這取大，否則取小
 * @param maxWeight 設定該堆最差的權重，一般設定為無窮大
 */
	public HeapSort(boolean Comparemode, float maxWeight) {
		this.vertexts = new IntArray();
		this.weight = new FloatArray();
		this.vertMap = new IntIntHashMap();
		this.Comparemode = Comparemode;
		this.maxWeight = maxWeight;
	}

	public boolean compared(float w1, float w2) {
		if (this.Comparemode) {
			if (w1 > w2) {
				return true;
			} else {
				return false;
			}
		} else {
			if (w1 < w2) {
				return true;
			} else {
				return false;
			}

		}
	}

	/**
	 * 方法是想堆中新增元素，並將該元素儲存在相應的位置
	 * 
	 * @param v
	 *            元素編號
	 * @param w
	 *            元素值
	 */
	public void addElement(int v, float w) {
		int i = this.vertMap.size();
		int k;
		this.vertexts.add(-1);
		this.weight.add(this.maxWeight);
		while (i > 0 && this.compared(w, this.weight.get(this.parent(i)))) {
			k = this.vertexts.get(this.parent(i));
			this.vertexts.set(i, k);
			this.weight.set(i, this.weight.get(this.parent(i)));
			this.vertMap.add(k, i);
			i = this.parent(i);
		}
		this.vertexts.set(i, v);
		this.weight.set(i, w);
		this.vertMap.add(v, i);

	}

	public float getBestCost() {
		return this.weight.get(0);
	}

	public int getBestVertex() {
		return this.vertexts.get(0);
	}
//移出最好的元素並將該最好的發回給使用者
	public int removeBestElemment() {
		if (this.vertexts.size() <= 0) {
			return -1;
		}
		int v = this.vertexts.get(0);
		this.vertMap.remove(v);
		this.vertexts.set(0, this.vertexts.get(this.vertexts.size() - 1));
		this.weight.set(0, this.weight.get(this.weight.size() - 1));
		// 此是因為this.vertexts.get(0)的位置還不確定，所以先付-1表示位置不確定
		this.vertMap.add(this.vertexts.get(0), -1);
		this.vertexts.remove(this.vertexts.size() - 1);
		this.weight.remove(this.weight.size() - 1);
		heapify(0);
		return v;
	}
//移除指定的元素
	public boolean removeElement(int v) {
		if (this.vertexts.size() != 0) {
			int i = this.vertMap.get(v);
			if (i == -1)
				return false;
			this.vertexts.set(i, this.vertexts.get(this.vertexts.size() - 1));
			this.weight.set(i, this.weight.get(this.weight.size() - 1));
			this.vertMap.add(this.vertexts.get(i), i);
			this.vertexts.remove(this.vertexts.size() - 1);
			this.weight.remove(this.weight.size() - 1);
			this.vertMap.remove(v);
			if (i <= this.vertexts.size() - 1) {
				heapify(i);
				Propogate(i);
			}
			return true;
		}
		return false;

	}
//更新你指定的元素資訊，當你更新的元素不存在時，則執行新增操作
	public int updateElement(int v, int w) {
		int i = this.vertMap.get(v);
		int k;
		if (i < 0) {
			this.addElement(v, w);
		} else {
			float w1 = this.weight.get(v);
			if (this.compared(w1, w)) {
				return 0;
			}
			while (i > 0 && this.compared(w1, this.weight.get(this.parent(i)))) {
				k = this.vertexts.get(this.parent(i));
				this.vertexts.set(i, k);
				this.weight.set(i, this.weight.get(k));
				this.vertMap.add(k, i);
				i = this.parent(i);
			}
			this.vertexts.set(i, v);
			this.weight.set(i, w);
			this.vertMap.add(v, i);
		}
		return 1;
	}
//調整某位置以後的元素，例如上面刪除了指定元素好，將要對元素在堆中的位置進行重新的調整，此時就要呼叫該函式
	private void heapify(int i) {
		int best = 0;
		int count = this.weight.size() - 1;
		int left = left(i);
		int right = right(i);
		if (left <= count
				&& this.compared(this.weight.get(left), this.weight.get(i))) {
			best = left;
		} else {
			best = i;
		}
		if (right <= count
				&& this.compared(this.weight.get(right), this.weight.get(best))) {
			best = right;
		}
		if (best != i) {
			swap(i, best);
			heapify(best);
		}

	}
//上面調整了後面的元素後，那麼該位置上面的父節點也要做相應的調整，此時需呼叫該函式
	private boolean Propogate(int v) {
		int v_parent = parent(v);
		while (v_parent > 0
				&& this.compared(this.weight.get(v_parent), this.weight.get(v))) {
			swap(v, v_parent);
			v = v_parent;
			v_parent = parent(v_parent);
		}
		return false;
	}
//調換操作，將某一位置的元素和某一位置的元素互換
	private void swap(int i, int j) {
		float wi = this.weight.get(i);
		int vi = this.vertexts.get(i);
		this.weight.set(i, this.weight.get(j));
		this.vertexts.set(i, this.vertexts.get(j));

		this.weight.set(j, wi);
		this.vertexts.set(j, vi);
		this.vertMap.add(this.vertexts.get(i), i);
		this.vertMap.add(this.vertexts.get(j), j);

	}
//得到某個位置節點的父節點位置
	private int parent(int i) {
		return ((i + 1) / 2) - 1;
	}
//得到某個節點左孩子位置
	private int left(int i) {
		return (2 * (i + 1)) - 1;
	}
//獲得右孩子位置
	private int right(int i) {
		return 2 * (i + 1);
	}
}
 

          該演算法實現上我使用了一個包，該包的功能和我們常使用的utils包的功能一樣，至不過，他們裡面的Map物件沒有put和set方法，它們均只有add,在add的時候會判斷集合中是否存在相同的key，如果存在這相當於set方法，如果不存在則相當與put方法，相應的jar包我會上傳到我在我的資源裡面，有興趣的可以下載下來，不需積分。在實現上額外的添加了一些方法如

public boolean removeElement(int v) 

public boolean compared(float w1, float w2) 
public int updateElement(int v, int w) 
 

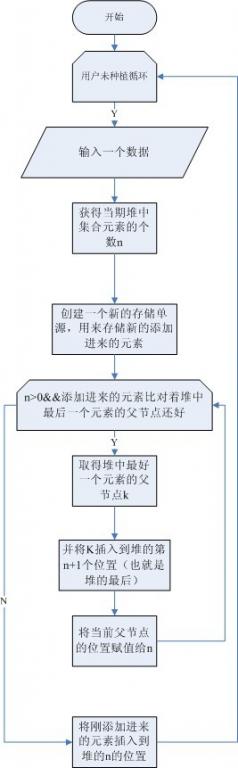
下面貼上處演算法的流程圖（只有新增元素的流程圖，具體的思想參照我上面的程式碼）：

        到此本文結束！謝謝瀏覽！歡迎評論，指出不足！