堆排序

一、概述

首先我們來看看什麼叫做堆排序？

若在輸出堆頂的最小值之後，使得剩餘的n-1個元素的序列重新又構成一個堆，則得到n個元素中的次小值，如此反覆，便能得到一個有序序列，稱這個過程為堆排序。

再來看看總結一下基本思想：

1. 將無序序列建成一個堆
2. 輸出堆頂的最小（大）值
3. 使剩餘的n-1個元素又調整成一個堆，則可得到n個元素的次小值
4. 重複執行，得到一個有序序列

通過上面的規律發現兩個問題，而堆排序需要解決這兩個問題：1.如何建堆？ 2.如何調整？

二、如何建堆

1.什麼是堆？

n個元素的序列{k1,k2,…,kn}，當且僅當滿足下列關係時，成為堆：

如果將序列看成一個完全二叉樹，非終端結點的值均小於或大於左右子結點的值。
利用樹的結構特徵來描述堆，所以樹只是作為堆的描述工具，堆實際是存放線上形空間中的。

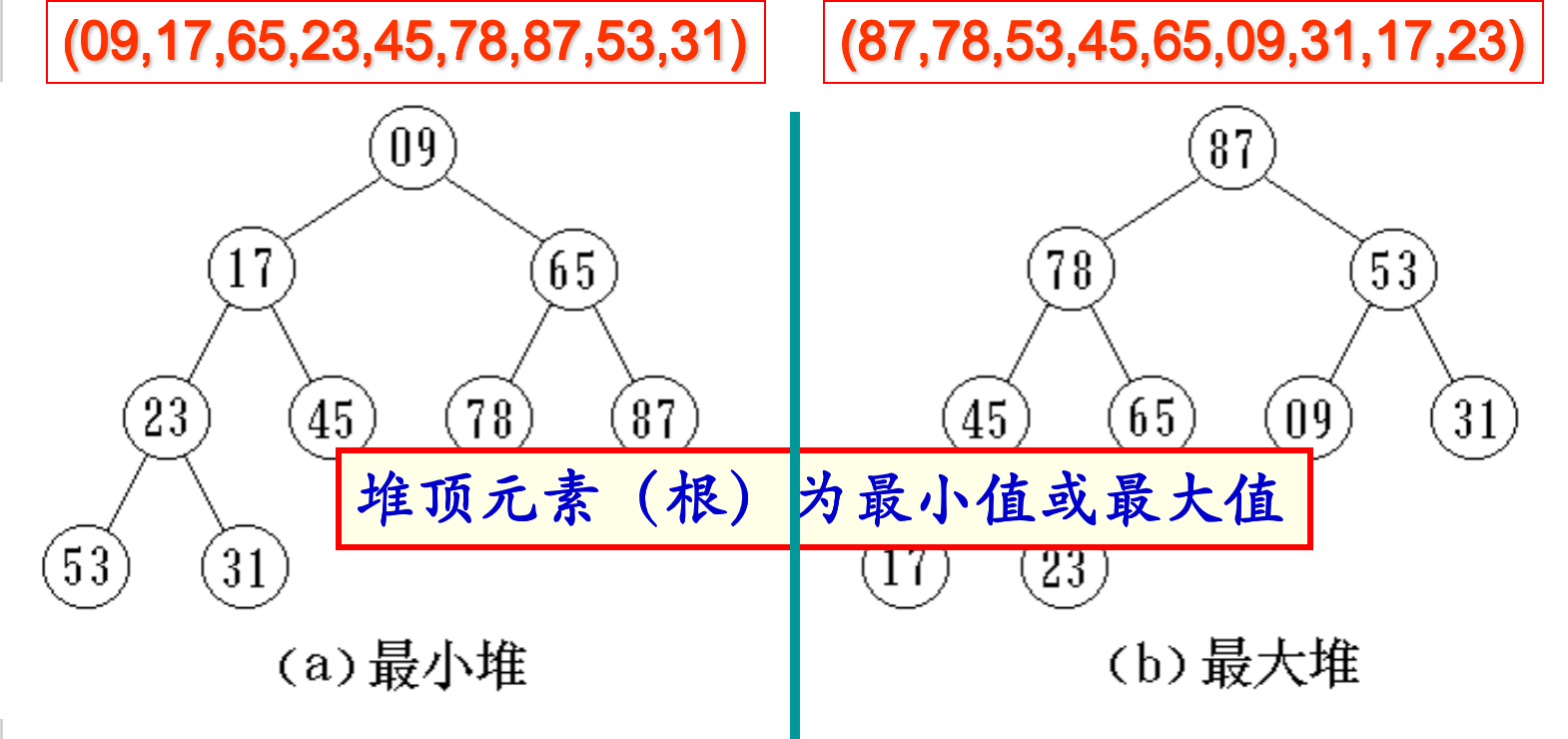
解釋： 從上面可以知道，當父節點大於左右孩子節點 或者父節點小於節點的時候，可以稱為堆，前者稱為大頂堆，後者稱為小頂堆。

2.建堆

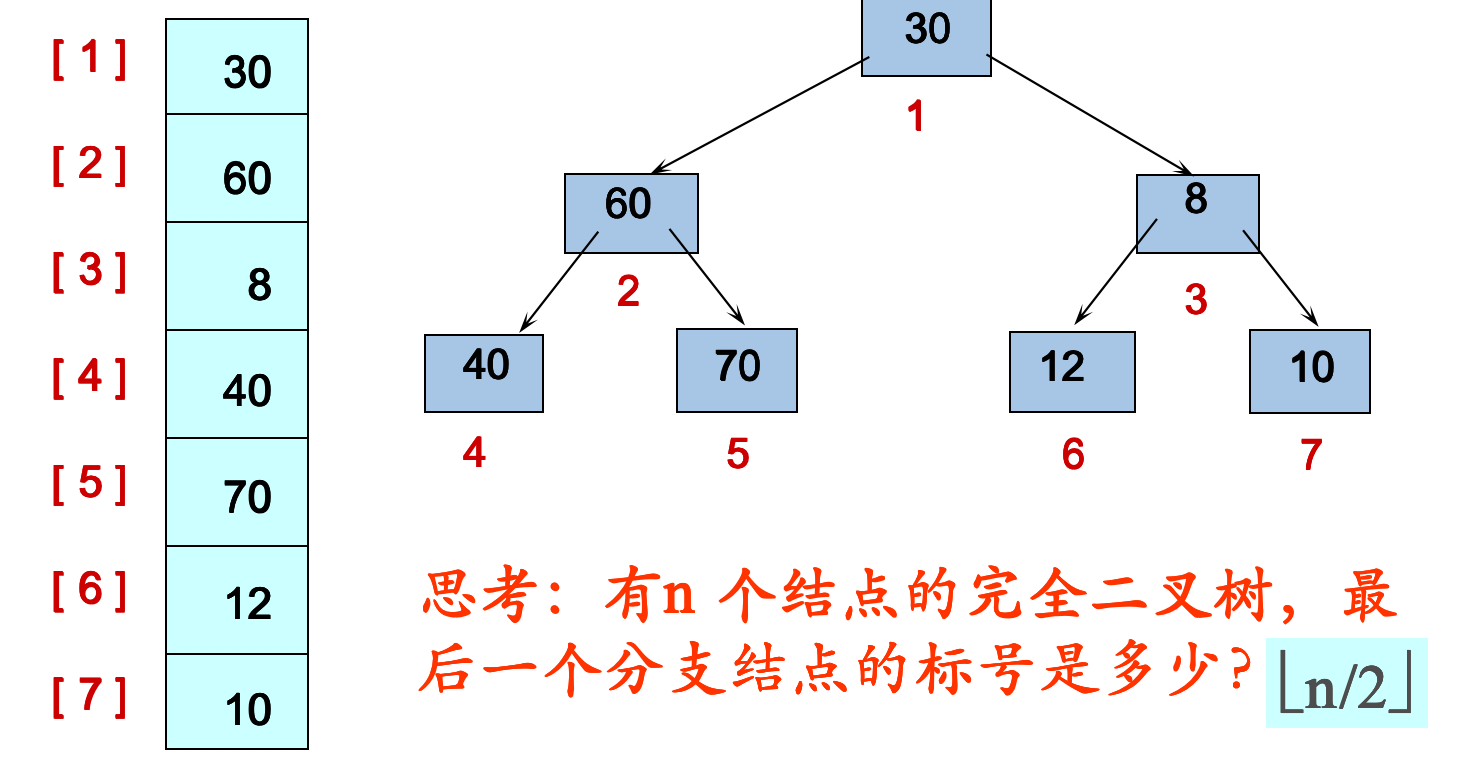
從第n/2 向下取整 個元素起，至第一個元素止，進行反覆篩選，如果我們要建立大頂堆，先比較左右孩子的大小，將比較大的孩子和父節點進行比較。

因為陣列的元素一共是7個元素，我們應該從第3個元素，首先我們應該比較第3個元素的左右孩子的大小，然後再進行調整。

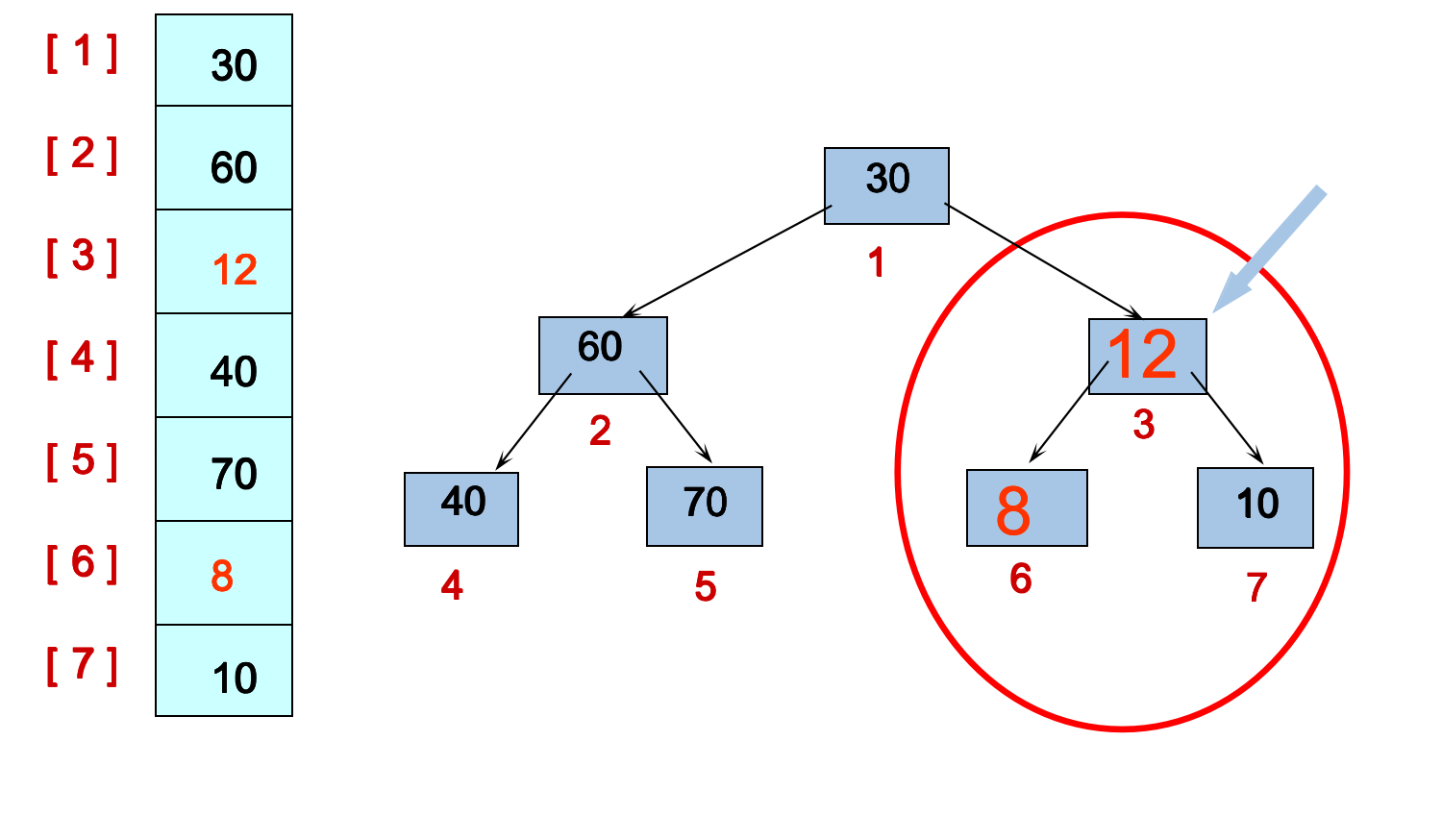
程式碼如下：

// 建立大頂堆
public void buildHeap(int[] arr){
 for (int i = arr.length / 2 - 1; i >= 0; i--) {
            //從第一個非葉子結點從下至上，從右至左調整結構
            adjustHeap(arr, i, arr.length);
        }
}
 /**
     * 調整大頂堆（僅是調整過程，建立在大頂堆已構建的基礎上）
     *
     * @param arr
     * @param i
     * @param length
     */
    public static void adjustHeap(int[] arr, int i, int length) {
        int temp = arr[i];//先取出當前元素i
        for (int k = i * 2 + 1; k < length; k = k * 2 + 1) {//從i結點的左子結點開始，也就是2i+1處開始
            if (k + 1 < length && arr[k] < arr[k + 1]) {//如果左子結點小於右子結點，k指向右子結點
                k++;
            }
            if (arr[k] > temp) {//如果子節點大於父節點，將子節點值賦給父節點（不用進行交換）
                arr[i] = arr[k];
                i = k;
            } else {
                break;
            }
        }
        arr[i] = temp;//將temp值放到最終的位置
    }

    /**
     * 交換元素
     *
     * @param arr
     * @param a
     * @param b
     */
    public static void swap(int[] arr, int a, int b) {
        int temp = arr[a];
        arr[a] = arr[b];
        arr[b] = temp;
    }
    
 

三、如何調整

當我們將陣列進行建立大頂堆或者小頂堆的時候，我們就會發現堆頂元素必然是該排序陣列的最大或者是最小的那個資料。如何在輸出堆頂元素後調整，使之成為新堆？

1. 輸出堆頂元素後，以堆中最後一個元素替代之
2. 將根結點與左、右子樹根結點比較，並與小者交換
3. 重複直至葉子結點，得到新的堆

解釋：
這時候我們將堆頂元素和最後一個元素進行交換，那麼我們調整前n-1個元素成堆，反覆操作即可

四、演算法分析

時間效率：$ O(nlog2n) $
空間效率：$ O（1）$
穩 定 性：不穩定
適用於n 較大的情況

五、完整程式碼

public class HeapSort {
    public static void main(String[] args) {
        int[] arr = {9, 8, 7, 6, 5, 4, 3, 2, 1};
        sort(arr);
        System.out.println(Arrays.toString(arr));
    }

    public static void sort(int[] arr) {
        //1.構建大頂堆
        for (int i = arr.length / 2 - 1; i >= 0; i--) {
            //從第一個非葉子結點從下至上，從右至左調整結構
            adjustHeap(arr, i, arr.length);
        }


        //2.調整堆結構+交換堆頂元素與末尾元素
        for (int j = arr.length - 1; j > 0; j--) {
            swap(arr, 0, j);//將堆頂元素與末尾元素進行交換
            adjustHeap(arr, 0, j);//重新對堆進行調整
        }

    }

    /**
     * 調整大頂堆（僅是調整過程，建立在大頂堆已構建的基礎上）
     *
     * @param arr
     * @param i
     * @param length
     */
    public static void adjustHeap(int[] arr, int i, int length) {
        int temp = arr[i];//先取出當前元素i
        for (int k = i * 2 + 1; k < length; k = k * 2 + 1) {//從i結點的左子結點開始，也就是2i+1處開始
            if (k + 1 < length && arr[k] < arr[k + 1]) {//如果左子結點小於右子結點，k指向右子結點
                k++;
            }
            if (arr[k] > temp) {//如果子節點大於父節點，將子節點值賦給父節點（不用進行交換）
                arr[i] = arr[k];
                i = k;
            } else {
                break;
            }
        }
        arr[i] = temp;//將temp值放到最終的位置
    }

    /**
     * 交換元素
     *
     * @param arr
     * @param a
     * @param b
     */
    public static void swap(int[] arr, int a, int b) {
        int temp = arr[a];
        arr[a] = arr[b];
        arr[b] = temp;
    }
}

歡迎關注個人公眾號：Coder辰砂