1，堆是什麼？

堆的邏輯結構是一顆完全二叉樹，但物理結構是順序表(一維陣列)。同時，此處的堆不要與JAVA記憶體分配中的堆記憶體混淆。這裡討論的是資料結構中的堆。

2，陣列實現堆的優勢及特點

由於堆從邏輯上看是一顆完全二叉樹，因此可以按照層序遍歷的順序將元素放入一維陣列中。注意為了方便，陣列的元素存放從索引 1 處開始（不是0）。採用陣列來存放就很容易地找到某個結點 i 的雙親結點(i/2)，孩子結點(左孩子：2i，右孩子：2i+1)

3，基於陣列的堆的實現需要哪些結構？

private T[] heap;//用來儲存堆元素的陣列
private int lastIndex;//最後一個元素的索引
 

private static final int DEFAULT_INITIAL_CAPACITY = 25;

首先需要一個一維陣列heap來儲存堆中的元素；其次，需要lastIndex標記堆中最後一個元素的索引，這樣也知道了堆中存放了多少個元素；最後，需要一個final靜態變數定義預設構造堆的大小。

4，JAVA中基於一維陣列的堆的實現具體程式碼分析

①建立堆，假設有N個元素，需要將這N個元素構建大頂堆，有兩種方法來建立堆。一種是通過add()方法，另一種是通過reheap()方法。現在分別討論如下：

對於add方法：當要向堆中新增新元素時，呼叫該方法完成新增元素的操作。那麼對這N個元素逐一呼叫add方法，就可以將這N個元素構造成大頂堆，此時的時間複雜度為O(nlogn)。add方法的程式碼如下：

public void add(T newEntry) {
        lastIndex++;
        if(lastIndex >= heap.length)
            doubleArray();//若堆空間不足，則堆大小加倍
        int newIndex = lastIndex;//從最後一個元素開始逐漸向上與父結點比較
        int parentIndex = newIndex / 2;
        heap[0] = newEntry;//哨兵
        while(newEntry.compareTo(heap[parentIndex]) > 0){
            heap[newIndex] 
 
= heap[parentIndex];
            newIndex = parentIndex;
            parentIndex = newIndex / 2;
        }
        heap[newIndex] = newEntry;
    }

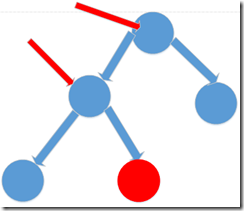
假設樹中有n個元素，則完全二叉樹高為logn，呼叫add方法的時間複雜度為O(logn)。向堆中插入新元素的具體操作如下：首先將元素陣列的最後一個位置，然後從該位置起向上調整，直至到根結點為止。

如圖，當插入新的紅色結點時，首先將它放在堆的末尾，然後進行再次堆調整(紅色箭頭所指)。

對於使用reheap方法來建立堆：N個元素邏輯上組成一顆完全二叉樹，從它的最後一個非葉子結點開始，逐漸向前調整，直至調整到根結點。對於每個被調整的結點，將以該結點為根的子樹調整成一個(子)堆。假設有8個元素的陣列，將將會從第4個元素起，開始進行堆調整(呼叫reheap方法)，直至調整到第 1 個元素為止。該方法建堆的時間複雜度為O(n)

reheap方法的程式碼如下：

/*
     * @Task:將樹根為rootIndex的半堆調整為新的堆，半堆：樹的左右子樹都是堆
     * @param rootIndex 以rootIndex為根的子樹
     */
    private void reheap(int rootIndex){
        boolean done = false;//標記堆調整是否完成
        T orphan = heap[rootIndex];
        int largeChildIndex = 2 * rootIndex;//預設左孩子的值較大
        //堆調整基於以largeChildIndex為根的子樹進行
        while(!done && (largeChildIndex <= lastIndex)){
            //largeChildIndex 標記rootIndex的左右孩子中較大的孩子
            int leftChildIndex = largeChildIndex;//預設左孩子的值較大
            int rightChildIndex = leftChildIndex + 1;
            //右孩子也存在,比較左右孩子
            if(rightChildIndex <= lastIndex && (heap[largeChildIndex].compareTo(heap[rightChildIndex] )< 0))
                largeChildIndex = rightChildIndex;
        //    System.out.println(heap[largeChildIndex]);//這裡有問題。。使用建構函式建立時reheap。。。。。
            if(orphan.compareTo(heap[largeChildIndex]) < 0){
                heap[rootIndex] = heap[largeChildIndex];
                rootIndex = largeChildIndex;
                largeChildIndex = 2 * rootIndex ;//總是預設左孩子的值較大
            }
            else//以rootIndex為根的子樹已經構成堆了
                done = true;
        }
        heap[rootIndex] = orphan;
    }

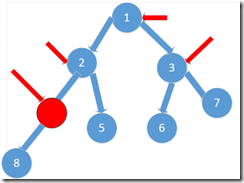
第4個元素就是最後一個非葉子結點。（紅色箭頭表示需要進行堆調整的結點）

兩種建堆方法的比較：

add方法合適於動態建堆，也就是說，來一個元素，呼叫add方法一次，再來一個元素，再呼叫add方法……直至構造了一個N個元素的堆。而對於reheap方法，它是先給定了N個元素，這N個元素表示成一顆完全二叉樹的形式，然後從樹的最後一個非葉子結點開始，依次往前調整，進而構造堆。

add方法的調整與reheap方法的調整是不相同的。add方法的整個調整過程如下：該元素被新增到了陣列最後一個位置lastIndex，然後，lastIndex與 (lastIndex / 2) 比較……即它總是與它的雙親結點比較。這一個元素調整完後，再來下一個元素，同樣先將它放到陣列最後，再與它的雙親比較……調整的方向是自下而上的。

reheap方法的調整過程如下：如上圖，第4號結點與它的孩子（第8號結點）比較，進行調整，使之滿足堆的定義。再接著是第3號結點與它的兩個孩子比較，進行調整。再接著是第2號結點與它的孩子比較（第4，5號結點），若有必要還得與第8號結點比較，……調整的方向是自上而下的。（上面已經提到，即 以從第4號結點開始，對該結點為根的子樹進行調整，將該子樹調整成一個堆）。

5，堆排序演算法的實現

對於一個排序演算法而言，首先得有一組可比較的資料拿來給你排序。故假設排序演算法需要一個裝有待排序資料的一維陣列 arr。這裡就有兩種方法來實現排序：

❶：根據待排序的資料(一維陣列 arr)建立一個堆，由於這裡可以採用第二種建堆方法（reheap方法），故建堆的時間複雜度為O(n)；空間複雜度也為O(n)，因為建立的堆本質上是個一維陣列，它就是由 n 個待排序資料組成的。

ArrayMaxHeap<Integer> heap = new ArrayMaxHeap<Integer>(arr);

然後，從 heap 中刪除元素時，將刪除的元素按順序放回到陣列arr中，直至將heap中的元素刪除完畢後全部放回到陣列arr中後，陣列arr就變成了有序的了。（堆的性質保證了每次從堆中刪除元素時總是刪除堆中最大的元素（即最大堆的堆頂元素））。由於每次從堆中刪除元素的時間複雜度為O(logn) ，故整個堆排序的時間複雜度為O(nlogn)、空間複雜度為O(n)。

❷： 第二種堆排序的實現方法如下：

還是根據給定的一維陣列arr 通過反覆呼叫reheap方法來建立堆。但是，是在arr上建立堆，而不是新開闢一個數組來建立堆。這樣，使得整個排序過程的空間複雜度為O(1)

由於是直接在 陣列arr 上建立堆，故堆建立的索引是從0開始，而不是從1開始了。

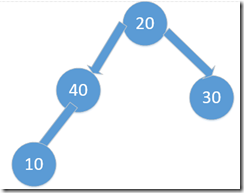
在arr陣列上建堆後，arr陣列中元素的順序就是符合堆定義的順序了（完全二叉樹中父結點的值比孩子結點的值要大）且第一個元素為最大元素；因為第一個元素為堆頂元素。因此，可以把 陣列arr 中的第一個元素與最後一個元素交換，這樣 arr 的前 n-1 個元素就構成了一個半堆（樹根的左右子樹都是堆稱為半堆），這樣就可以進行reheap操作將前n-1個元素重新調整成堆。

下圖就是一個半堆，根結點20的左右子樹都是堆，但整個完全二叉樹不是堆。

接著，又將第一個元素與倒數第二個元素交換，剩下的前n-2個元素構成了一個半堆，又進行reheap操作將之調整為堆……反覆執行上述步驟即可將arr排序。

由於該方法是直接在arr上建堆並排序的。故空間複雜度為O(1)，而每次執行reheap方法的時間複雜度為O(logn)，共有n個元素，需要執行n次reheap，故整個堆排序的時間複雜度為O(nlogn)，空間複雜度為O(1)。

關於時間複雜度的分析 有個小問題：第一次reheap方法需要調整的半堆有n-1個元素，第二次reheap方法調整的半堆有n-2個元素……，也就是說，每次reheap所需要執行的調整次數是越來越少的。但總的時間複雜度還是O(nlogn)了。