分治法-大整數乘法
問題分析:
在計算機上處理一些大資料相乘時,由於計算機硬體的限制,不能直接進行相乘得到想要的結果。可以將一個大的整數乘法分而治之,將大問題變成小問題,變成簡單的小數乘法再進行合併,從而解決上述問題。

當分解到只有一位數時,乘法就很簡單了。
演算法設計:
分解:
首先將2個大整數a(n位)、b(m位)分解為兩部分:ah和al、bh和bl
ah表示大整數a的高位,al表示大整數a的低位,,ah、al為n/2位。
bh表示大整數b的高位,bl表示大整數b的低位,,bh、bl為m/2位。
2個大整數a(n位)、b(m位)相乘轉換成了4個乘法運算ah*bh、ah*bl、al*bh、al*bl,而乘數的位數
求解子問題:
繼續分解兩個乘法運算,直到分解有一個乘數位1位數時停止分解,進行乘法運算並記錄結果。
合併:
將計算出的結果相加並回溯,求出最終結果。
#include<stdlib.h> #include<cstring> #include <iostream> using namespace std; #define M 100 char sa[1000]; char sb[1000]; typedef struct _Node { int s[M]; int l; int c; } Node, *pNode; void cp(pNode src, pNode des, int st, int l) { int i, j; for (i = st, j = 0; i < st + 1; i++, j++) { des->s[j] = src->s[i]; } des->l = l; des->c = st + src->c; } void add(pNode pa, pNode pb, pNode ans) { int i, cc, k, palen, pblen, len; int ta, tb; pNode temp; if ((pa->c < pb->c)) { temp = pa; pa = pb; pb = temp; } ans->c = pb->c; cc = 0; palen = pa->l + pa->c; pblen = pb->l + pb->c; if (palen > pblen) len = palen; else len = pblen; k = pa->c - pb->c; for (i = 0; i < len - ans->c; i++) { if (i < k) ta = 0; else ta = pa->s[i - k]; if (i < pb->l) tb = pb->s[i]; else tb = 0; if (i >= pa->l + k) ta = 0; ans->s[i] = (ta + tb + cc) % 10; cc = (ta + tb + cc) / 10; } if (cc) ans->s[i++] = cc; ans->l = i; } void mul(pNode pa, pNode pb, pNode ans) { int i, cc, w; int ma = pa->l >> 1, mb = pb->l >> 1; Node ah, al, bh, bl; Node t1, t2, t3, t4, z; pNode temp; if (!ma || !mb) { if (!ma) { temp = pa; pa = pb; pb = temp; } ans->c = pa->c + pb->c; w = pb->s[0]; cc = 0; for (i = 0; i < pa->l; i++) { ans->s[i] = (w * pa->s[i] + cc) % 10; cc = (w * pa->s[i] + cc) / 10; } if (cc) ans->s[i++] = cc; ans->l = i; return; } cp(pa, &ah, ma, pa->l - ma); cp(pa, &al, 0, ma); cp(pb, &bh, mb, pb->l - mb); cp(pb, &bl, 0, mb); mul(&ah, &bh, &t1); mul(&ah, &bl, &t2); mul(&al, &bh, &t3); mul(&al, &bl, &t4); add(&t3, &t4, ans); add(&t2, ans, &z); add(&t1, &z, ans); } int main() { Node ans, a, b; cout << "輸入大整數 a:" << endl; cin >> sa; cout << "輸入大整數 b:" << endl; cin >> sb; a.l = strlen(sa); b.l = strlen(sb); int z = 0, i; for (i = a.l - 1; i >= 0; i--) a.s[z++] = sa[i] - '0'; a.c = 0; z = 0; for (i = b.l - 1; i >= 0; i--) b.s[z++] = sb[i] - '0'; b.c = 0; mul(&a, &b, &ans); cout << "最終結果為:"; for (i = ans.l - 1; i >= 0; i--) cout << ans.s[i]; cout << endl; return 0; }
程式碼解釋:
1、將兩個輸入的大數,倒序儲存在陣列s[]中,l表示長度,c表示冪,c初始為0。
2、cp函式:將一個n位的數,分成兩個n/2的數並存儲,記錄它的長度和次冪。
3、mul函式,不斷地分解,直到有一個乘數為1位數時停止分解,進行乘法並記錄結果。
4、add函式,將分解得到的數,進行相加合併。
程式碼流程:
初始化:將a、b倒序儲存在陣列a.s[],b.s[]中。
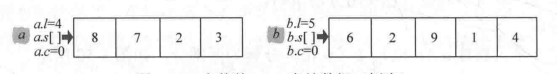
分解:cp函式:將一個n位的數,分成兩個n/2的數並存儲,記錄它的長度和次冪。ah表示高位,al表示低位,l用來表示數的長度,c表示次冪。
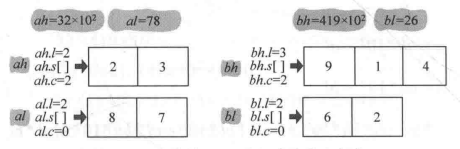
轉換為4次乘法運算:ah*bh,ah*bl,al*bh,al*bl:

求解子問題:
ah*bh,ah*bl,al*bh,al*bl

繼續求解子問題:
上述4個乘法運算都有一個乘數為1位數,可以直接進行乘法運算。以ahh*bhh為例:
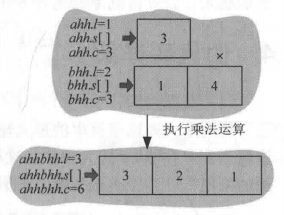 3首先和1相乘得到3儲存在下面陣列的第0位,然後3和4相乘得到12,先儲存12%10=2,然後儲存進位12/10=1,那樣結果就為倒序的321,結果的次冪是兩個乘數次冪之和。
3首先和1相乘得到3儲存在下面陣列的第0位,然後3和4相乘得到12,先儲存12%10=2,然後儲存進位12/10=1,那樣結果就為倒序的321,結果的次冪是兩個乘數次冪之和。
4個乘法運算結果如下圖:
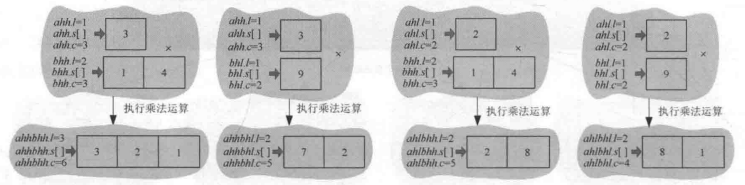
合併:
合併子問題結果,返回給ah*bh,將上面4個乘法運算的結果加起來返回給ah*bh。

由此得到ah*bh=13408x10^4。
用同樣的方法求得ah*bl=832x10^2,al*bh=32682x10^2,al*bl=2028。將這4個子問題結果加起來,合併得到原問題a*b=137433428。
演算法複雜度分析:
假設兩個n位大整數相乘的時間複雜度為T(n),則:
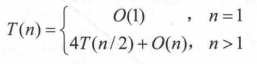
當n>1時,可以遞推求解如下:

遞推最終的規模為1,令n=2^x,則x=logn,那麼有:
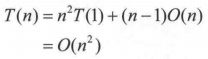
大整數乘法的時間複雜度為O(n^2)。
空間複雜度:
程式中變數佔用了一些輔助空間,都是常數階,但合併時結點陣列佔用的輔助空間為O(n),遞迴呼叫所使用的棧空間時O(logn)。所以,空間複雜度為O(n)。
