（注：本文譯自一篇部落格，作者行文較隨意，我儘量按原意翻譯，但作者所介紹的知識還是非常好的，包括例子的選擇、理論的介紹都很到位，由淺入深，源文地址）

　　近些年來，人工智慧領域又活躍起來，除了傳統了學術圈外，Google、Microsoft、facebook等工業界優秀企業也紛紛成立相關研究團隊，並取得了很多令人矚目的成果。這要歸功於社交網路使用者產生的大量資料，這些資料大都是原始資料，需要被進一步分析處理；還要歸功於廉價而又強大的計算資源的出現，比如GPGPU的快速發展。

　　除去這些因素，AI尤其是機器學習領域出現的一股新潮流很大程度上推動了這次復興——深度學習。本文中我將介紹深度學習背後的關鍵概念及演算法，從最簡單的元素開始並以此為基礎進行下一步構建。

　　（本文作者也是Java deep learning library的作者，可以從此處獲得，本文中的例子就是使用這個庫實現的。如果你喜歡，可以在Github上給個星~。用法介紹也可以從此處獲得）

機器學習基礎

　　如果你不太熟悉相關知識，通常的機器學習過程如下：

　　　　1、機器學習演算法需要輸入少量標記好的樣本，比如10張小狗的照片，其中1張標記為1（意為狗）其它的標記為0（意為不是狗）——本文主要使用監督式、二叉分類。

　　　　2、這些演算法“學習”怎麼樣正確將狗的圖片分類，然後再輸入一個新的圖片時，可以期望演算法輸出正確的圖片標記（如輸入一張小狗圖片，輸出1；否則輸出0）。

　　這通常是難以置信的：你的資料可能是模糊的，標記也可能出錯；或者你的資料是手寫字母的圖片，用其實際表示的字母來標記它。

感知機

　　感知機是最早的監督式訓練演算法，是神經網路構建的基礎。

　　假如平面中存在 n 個點，並被分別標記為“0”和“1”。此時加入一個新的點，如果我們想知道這個點的標記是什麼（和之前提到的小狗圖片的辨別同理），我們要怎麼做呢？

　　一種很簡單的方法是查詢離這個點最近的點是什麼，然後返回和這個點一樣的標記。而一種稍微“智慧”的辦法則是去找出平面上的一條線來將不同標記的資料點分開，並用這條線作為“分類器”來區分新資料點的標記。

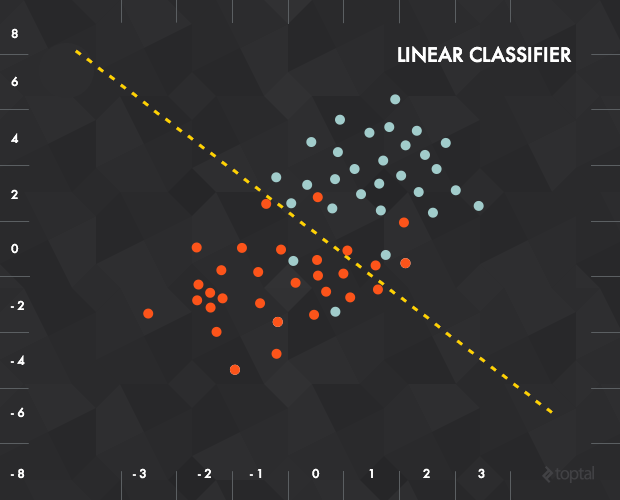
　　在本例中，每一個輸入資料都可以表示為一個向量 x = (x_1, x_2) ，而我們的函式則是要實現“如果線以下，輸出0；線以上，輸出1”。

　　用數學方法表示，定義一個表示權重的向量 w 和一個垂直偏移量 b。然後，我們將輸入、權重和偏移結合可以得到如下傳遞函式：

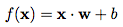
　　這個傳遞函式的結果將被輸入到一個啟用函式中以產生標記。在上面的例子中，我們的啟用函式是一個門限截止函式（即大於某個閾值後輸出1）：

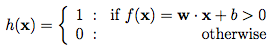
訓練

　　感知機的訓練包括多訓練樣本的輸入及計算每個樣本的輸出。在每一次計算以後，權重 w 都要調整以最小化輸出誤差，這個誤差由輸入樣本的標記值與實際計算得出值的差得出。還有其它的誤差計算方法，如均方差等，但基本的原則是一樣的。

缺陷

　　這種簡單的感知機有一個明顯缺陷：只能學習線性可分函式。這個缺陷重要嗎？比如 XOR，這麼簡單的函式，都不能被線性分類器分類（如下圖所示，分隔兩類點失敗）：

　　為了解決這個問題，我們要使用一種多層感知機，也就是——前饋神經網路：事實上，我們將要組合一群這樣的感知機來創建出一個更強大的學習機器。

前饋神經網路

　　神經網路實際上就是將大量之前講到的感知機進行組合，用不同的方法進行連線並作用在不同的啟用函式上。

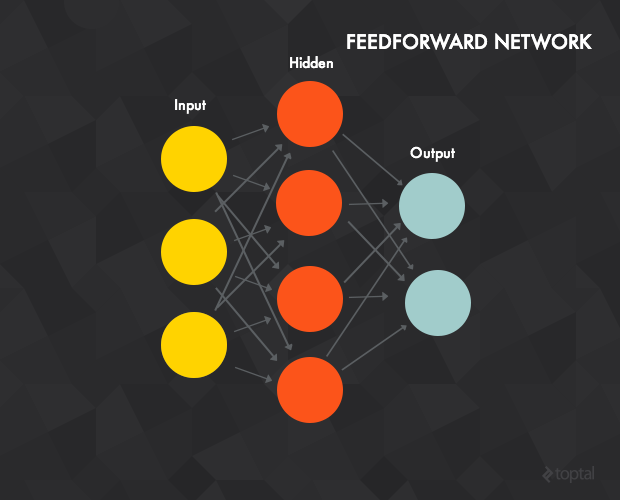
　　我們簡單介紹下前向神經網路，其具有以下屬性：

• 一個輸入層，一個輸出層，一個或多個隱含層。上圖所示的神經網路中有一個三神經元的輸入層、一個四神經元的隱含層、一個二神經元的輸出層。
• 每一個神經元都是一個上文提到的感知機。
• 輸入層的神經元作為隱含層的輸入，同時隱含層的神經元也是輸出層神經元的輸入。
• 每條建立在神經元之間的連線都有一個權重 w （與感知機中提到的權重類似）。
• 在 t 層的每個神經元通常與前一層（ t - 1層）中的每個神經元都有連線（但你可以通過將這條連線的權重設為0來斷開這條連線）。
• 為了處理輸入資料，將輸入向量賦到輸入層中。在上例中，這個網路可以計算一個3維輸入向量（由於只有3個輸入層神經元）。假如輸入向量是 [7, 1, 2]，你將第一個輸入神經元輸入7，中間的輸入1，第三個輸入2。這些值將被傳播到隱含層，通過加權傳遞函式傳給每一個隱含層神經元（這就是前向傳播），隱含層神經元再計算輸出（啟用函式）。
• 輸出層和隱含層一樣進行計算，輸出層的計算結果就是整個神經網路的輸出。

超線性

　　如果每一個感知機都只能使用一個線性啟用函式會怎麼樣？整個網路的最終輸出也仍然是將輸入資料通過一些線性函式計算過一遍，只是用一些在網路中收集的不同權值調整了一下。換名話說，再多線性函式的組合還是線性函式。如果我們限定只能使用線性啟用函式的話，前饋神經網路其實比一個感知機強大不到哪裡去，無論網路有多少層。

　　正是這個原因，大多數神經網路都是使用的非線性啟用函式，如對數函式、雙曲正切函式、階躍函式、整流函式等。不用這些非線性函式的神經網路只能學習輸入資料的線性組合。

訓練

大多數常見的應用在多層感知機的監督式訓練的演算法都是反向傳播演算法。基本的流程如下：

　　1、將訓練樣本通過神經網路進行前向傳播計算。

　　2、計算輸出誤差，常用均方差：

　　　　其中 t 是目標值， y 是實際的神經網路計算輸出。其它的誤差計算方法也可以，但MSE（均方差）通常是一種較好的選擇。

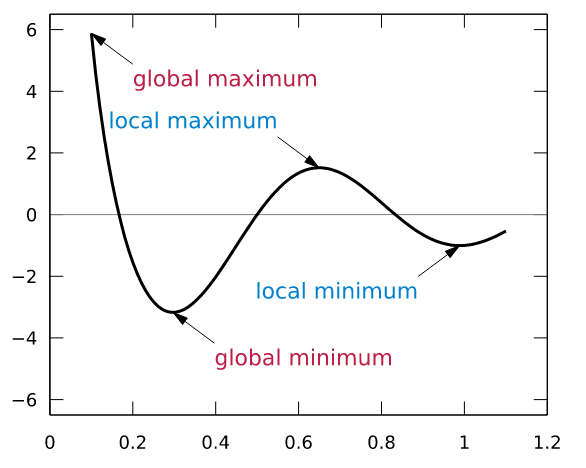
　　3、網路誤差通過隨機梯度下降的方法來最小化。

　　梯度下降很常用，但在神經網路中，輸入引數是一個訓練誤差的曲線。每個權重的最佳值應該是誤差曲線中的全域性最小值（上圖中的 global minimum）。在訓練過程中，權重以非常小的步幅改變（在每個樣本或每小組樣本訓練完成後）以找到全域性最小值，但這可不容易，訓練通常會結束在區域性最小值上（上圖中的local minima）。如例子中的，如果當前權重值為0.6，那麼要向0.4方向移動。

　　這個圖表示的是最簡單的情況，誤差只依賴於單個引數。但是，網路誤差依賴於每一個網路權重，誤差函式非常、非常複雜。

　　好訊息是反向傳播演算法提供了一種通過利用輸出誤差來修正兩個神經元之間權重的方法。關係本身十分複雜，但對於一個給定結點的權重修正按如下方法（簡單）：

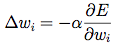
　　其中 E 是輸出誤差， w_i 是輸入 i 的權重。

　　實質上這麼做的目的是利用權重 i 來修正梯度的方向。關鍵的地方在於誤差的導數的使用，這可不一定好計算：你怎麼樣能給一個大型網路中隨機一個結點中的隨機一個權重求導數呢？

　　答案是：通過反向傳播。誤差的首次計算很簡單（只要對預期值和實際值做差即可），然後通過一種巧妙的方法反向傳回網路，讓我們有效的在訓練過程中修正權重並（期望）達到一個最小值。

隱含層

　　隱含層十分有趣。根據普適逼近原理，一個具有有限數目神經元的隱含層可以被訓練成可逼近任意隨機函式。換句話說，一層隱含層就強大到可以學習任何函數了。這說明我們在多隱含層（如深度網路）的實踐中可以得到更好的結果。

　　隱含層儲存了訓練資料的內在抽象表示，和人類大腦（簡化的類比）儲存有對真實世界的抽象一樣。接下來，我們將用各種方法來搞一下這個隱含層。

一個網路的例子

　　可以看一下這個通過 testMLPSigmoidBP 方法用Java實現的簡單(4-2-3)前饋神經網路，它將 IRIS 資料集進行了分類。這個資料集中包含了三類鳶尾屬植物，特徵包括花萼長度，花瓣長度等等。每一類提供50個樣本給這個神經網路訓練。特徵被賦給輸入神經元，每一個輸出神經元代表一類資料集（“1/0/0” 表示這個植物是Setosa，“0/1/0”表示 Versicolour，而“0/0/1”表示 Virginica）。分類的錯誤率是2/150（即每分類150個，錯2個）。

大規模網路中的難題

　　神經網路中可以有多個隱含層：這樣，在更高的隱含層裡可以對其之前的隱含層構建新的抽象。而且像之前也提到的，這樣可以更好的學習大規模網路。增加隱含層的層數通常會導致兩個問題：

　　　　1、梯度消失：隨著我們新增越來越多的隱含層，反向傳播傳遞給較低層的資訊會越來越少。實際上，由於資訊向前反饋，不同層次間的梯度開始消失，對網路中權重的影響也會變小。

　　　　2、過度擬合：也許這是機器學習的核心難題。簡要來說，過度擬合指的是對訓練資料有著過於好的識別效果，這時導至模型非常複雜。這樣的結果會導致對訓練資料有非常好的識別較果，而對真實樣本的識別效果非常差。

　　下面我們來看看一些深度學習的演算法是如何面對這些難題的。

自編碼器

大多數的機器學習入門課程都會讓你放棄前饋神經網路。但是實際上這裡面大有可為——請接著看。

　　自編碼器就是一個典型的前饋神經網路，它的目標就是學習一種對資料集的壓縮且分散式的表示方法（編碼思想）。

　　從概念上講，神經網路的目的是要訓練去“重新建立”輸入資料，好像輸入和目標輸出資料是一樣的。換句話說：你正在讓神經網路的輸出與輸入是同一樣東西，只是經過了壓縮。這還是不好理解，先來看一個例子。

壓縮輸入資料：灰度影象

　　這裡有一個由28x28畫素的灰度影象組成的訓練集，且每一個畫素的值都作為一個輸入層神經元的輸入（這時輸入層就會有784個神經元）。輸出層神經元要有相同的數目（784），且每一個輸出神經元的輸出值和輸入影象的對應畫素灰度值相同。

　　在這樣的演算法架構背後，神經網路學習到的實際上並不是一個訓練資料到標記的“對映”，而是去學習資料本身的內在結構和特徵（也正是因為這，隱含層也被稱作特徵探測器(feature detector)）。通常隱含層中的神經元數目要比輸入/輸入層的少，這是為了使神經網路只去學習最重要的特徵並實現特徵的降維。

　　我們想在中間層用很少的結點去在概念層上學習資料、產生一個緊緻的表示方法。

流行感冒

　　為了更好的描述自編碼器，再看一個應用。

　　這次我們使用一個簡單的資料集，其中包括一些感冒的症狀。如果感興趣，這個例子的原始碼釋出在這裡。

　　資料結構如下：

• • 輸入資料一共六個二進位制位
  • 前三位是病的證狀。例如，1 0 0 0 0 0 代表病人發燒；0 1 0 0 0 0 代表咳嗽；1 1 0 0 0 0 代表即咳嗽又發燒等等。
  • 後三位表示抵抗能力，如果一個病人有這個，代表他/她不太可能患此病。例如，0 0 0 1 0 0 代表病人接種過流感疫苗。一個可能的組合是：0 1 0 1 0 0 ，這代表著一個接種過流感疫苗的咳嗽病人，等等。

　　當一個病人同時擁用前三位中的兩位時，我們認為他生病了；如果至少擁用後三位中的兩位，那麼他是健康的，如：

• • 111000, 101000, 110000, 011000, 011100 = 生病
  • 000111, 001110, 000101, 000011, 000110 = 健康

　　我們來訓練一個自編碼器（使用反向傳播），六個輸入、六個輸出神經元，而只有兩個隱含神經元。

　　在經過幾百次迭代以後，我們發現，每當一個“生病”的樣本輸入時，兩個隱含層神經元中的一個（對於生病的樣本總是這個）總是顯示出更高的啟用值。而如果輸入一個“健康”樣本時，另一個隱含層則會顯示更高的啟用值。

再看學習

　　本質上來說，這兩個隱含神經元從資料集中學習到了流感症狀的一種緊緻表示方法。為了檢驗它是不是真的實現了學習，我們再看下過度擬合的問題。通過訓練我們的神經網路學習到的是一個緊緻的簡單的，而不是一個高度複雜且對資料集過度擬合的表示方法。

　　某種程度上來講，與其說在找一種簡單的表示方法，我們更是在嘗試從“感覺”上去學習資料。

受限波爾茲曼機

　　下一步來看下受限波爾茲曼機（Restricted Boltzmann machines RBM），一種可以在輸入資料集上學習概率分佈的生成隨機神經網路。

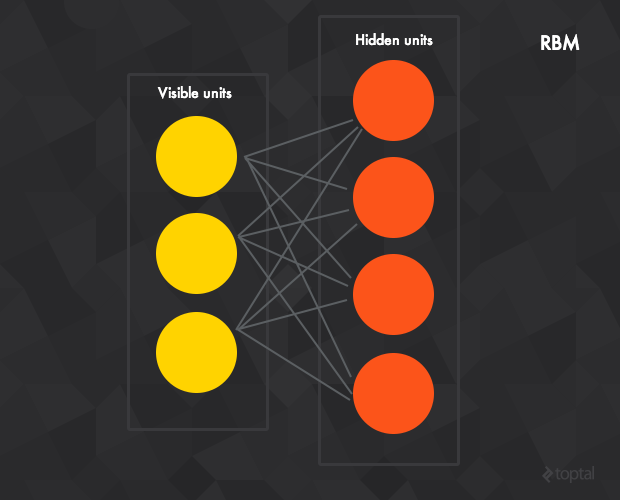
　　RBM由隱含層、可見層、偏置層組成。和前饋神經網路不同，可見層和隱含層之間的連線是無方向性（值可以從可見層->隱含層或隱含層->可見層任意傳輸）且全連線的（每一個當前層的神經元與下一層的每個神經元都有連線——如果允許任意層的任意神經元連線到任意層去，我們就得到了一個波爾茲曼機（非受限的））。

　　標準的RBM中，隱含和可見層的神經元都是二態的（即神經元的啟用值只能是服從伯努力分佈的0或1），不過也存在其它非線性的變種。

　　雖然學者們已經研究RBM很長時間了，最近出現的對比差異無監督訓練演算法使這個領域復興。

對比差異

　　單步對比差異演算法原理：

　　1、正向過程：

• • 輸入樣本 v 輸入至輸入層中。
  • v 通過一種與前饋網路相似的方法傳播到隱含層中，隱含層的啟用值為 h。

　　2、反向過程：

• • 將 h 傳回可見層得到 v’ （可見層和隱含層的連線是無方向的，可以這樣傳）。
  • 再將 v’ 傳到隱含層中，得到 h’。

　　3、權重更新：

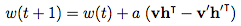
　　　　其中 a 是學習速率， v, v’, h, h’ 和 w 都是向量。

　　演算法的思想就是在正向過程中影響了網路的內部對於真實資料的表示。同時，反向過程中嘗試通過這個被影響過的表示方法重建資料。主要目的是可以使生成的資料與原資料儘可能相似，這個差異影響了權重更新。

　　換句話說，這樣的網路具有了感知對輸入資料表示的程度的能力，而且嘗試通過這個感知能力重建資料。如果重建出來的資料與原資料差異很大，那麼進行調整並再次重建。

再看流行感冒的例子

　　為了說明對比差異，我們使用與上例相同的流感症狀的資料集。測試網路是一個包含6個可見層神經元、2個隱含層神經元的RBM。我們用對比差異的方法對網路進行訓練，將症狀 v 賦到可見層中。在測試中，這些症狀值被重新傳到可見層；然後再被傳到隱含層。隱含層的神經元表示健康/生病的狀態，與自編碼器相似。

　　在進行過幾百次迭代後，我們得到了與自編碼器相同的結果：輸入一個生病樣本，其中一個隱含層神經元具有更高啟用值；輸入健康的樣本，則另一個神經元更興奮。

　　例子的程式碼在這裡。

深度網路

　　到現在為止，我們已經學習了隱含層中強大的特徵探測器——自編碼器和RBM，但現在還沒有辦法有效的去利用這些功能。實際上，上面所用到的這些資料集都是特定的。而我們要找到一些方法來間接的使用這些探測出的特徵。

　　好訊息是，已經發現這些結構可以通過棧式疊加來實現深度網路。這些網路可以通過貪心法的思想訓練，每次訓練一層，以克服之前提到在反向傳播中梯度消失及過度擬合的問題。

　　這樣的演算法架構十分強大，可以產生很好的結果。如Google著名的“貓”識別，在實驗中通過使用特定的深度自編碼器，在無標記的圖片庫中學習到人和貓臉的識別。

　　下面我們將更深入。

棧式自編碼器

　　和名字一樣，這種網路由多個棧式結合的自編碼器組成。

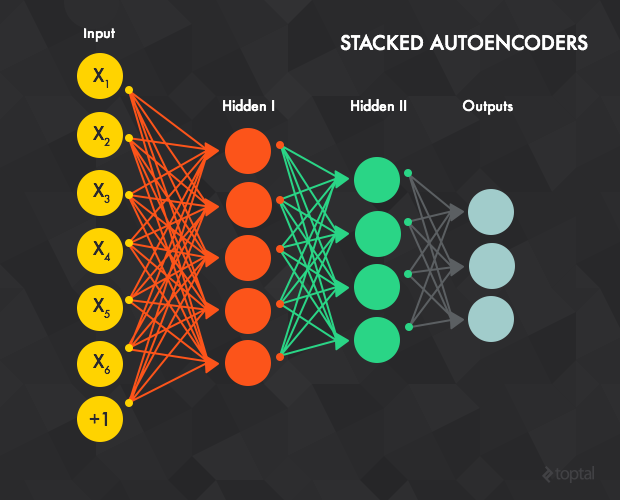
　　自編碼器的隱含層 t 會作為 t + 1 層的輸入層。第一個輸入層就是整個網路的輸入層。利用貪心法訓練每一層的步驟如下：

　　　　1、通過反向傳播的方法利用所有資料對第一層的自編碼器進行訓練（t=1，上圖中的紅色連線部分）。

　　　　2、訓練第二層的自編碼器 t=2 （綠色連線部分）。由於 t=2 的輸入層是 t=1 的隱含層，我們已經不再關心 t=1 的輸入層，可以從整個網路中移除。整個訓練開始於將輸入樣本資料賦到 t=1 的輸入層，通過前向傳播至 t = 2 的輸出層。下面t = 2的權重（輸入->隱含和隱含->輸出）使用反向傳播的方法進行更新。t = 2的層和 t=1 的層一樣，都要通過所有樣本的訓練。

　　　　3、對所有層重複步驟1-2（即移除前面自編碼器的輸出層，用另一個自編碼器替代，再用反向傳播進行訓練）。

　　　　4、步驟1-3被稱為預訓練，這將網路裡的權重值初始化至一個合適的位置。但是通過這個訓練並沒有得到一個輸入資料到輸出標記的對映。例如，一個網路的目標是被訓練用來識別手寫數字，經過這樣的訓練後還不能將最後的特徵探測器的輸出（即隱含層中最後的自編碼器）對應到圖片的標記上去。這樣，一個通常的辦法是在網路的最後一層（即藍色連線部分）後面再加一個或多個全連線層。整個網路可以被看作是一個多層的感知機，並使用反向傳播的方法進行訓練（這步也被稱為微調）。

　　棧式自編碼器，提供了一種有效的預訓練方法來初始化網路的權重，這樣你得到了一個可以用來訓練的複雜、多層的感知機。

深度信度網路

　　和自編碼器一樣，我也可以將波爾茲曼機進行棧式疊加來構建深度信度網路（DBN）。

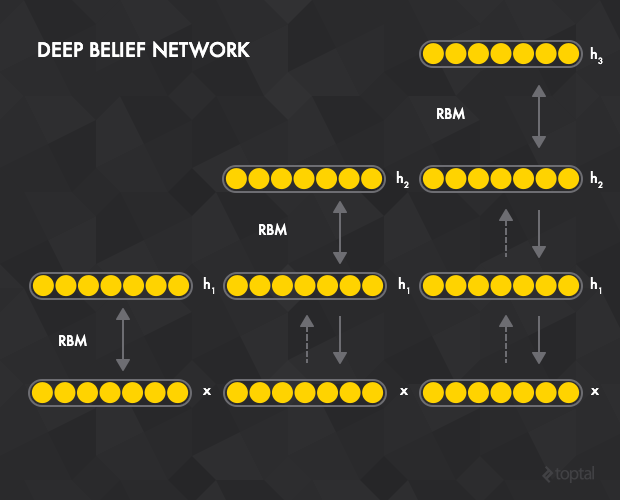
　　在本例中，隱含層 RBM t 可以看作是 RBM t+1 的可見層。第一個RBM的輸入層即是整個網路的輸入層，層間貪心式的預訓練的工作模式如下：

　　　　1. 通過對比差異法對所有訓練樣本訓練第一個RBM t=1 

　　　　2. 訓練第二個RBM t=1。由於 t=2 的可見層是 t=1 的隱含層，訓練開始於將資料賦至 t=1 的可見層，通過前向傳播的方法傳至 t=1 的隱含層。然後作為 t=2 的對比差異訓練的初始資料。

　　　　3. 對所有層重複前面的過程。

　　　　4. 和棧式自編碼器一樣，通過預訓練後，網路可以通過連線到一個或多個層間全連線的 RBM 隱含層進行擴充套件。這構成了一個可以通過反向傳僠進行微調的多層感知機。

　　本過程和棧式自編碼器很相似，只是用RBM將自編碼器進行替換，並用對比差異演算法將反向傳播進行替換。

　　(注: 例中的原始碼可以從 此處獲得.)

卷積網路

　　這個是本文最後一個軟體架構——卷積網路，一類特殊的對影象識別非常有效的前饋網路。

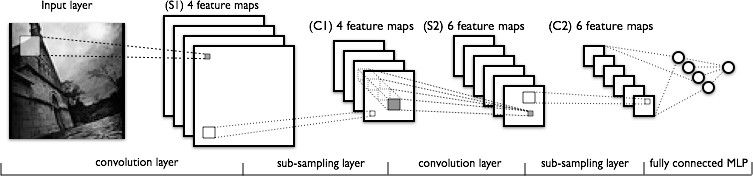
　　在我們深入看實際的卷積網路之臆，我們先定義一個影象濾波器，或者稱為一個賦有相關權重的方陣。一個濾波器可以應用到整個圖片上，通常可以應用多個濾波器。比如，你可以應用四個6x6的濾波器在一張圖片上。然後，輸出中座標（1,1）的畫素值就是輸入影象左上角一個6x6區域的加權和，其它畫素也是如此。

　　有了上面的基礎，我們來介紹定義出卷積網路的屬性：

• 卷積層  對輸入資料應用若干濾波器。比如影象的第一卷積層使用4個6x6濾波器。對影象應用一個濾波器之後的得到的結果被稱為特徵圖譜（feature map, FM），特徵圖譜的數目和濾波器的數目相等。如果前驅層也是一個卷積層，那麼濾波器應用在FM上，相當於輸入一個FM，輸出另外一個FM。從直覺上來講，如果將一個權重分佈到整個影象上後，那麼這個特徵就和位置無關了，同時多個濾波器可以分別探測出不同的特徵。
• 下采樣層 縮減輸入資料的規模。例如輸入一個32x32的影象，並且通過一個2x2的下采樣，那麼可以得到一個16x16的輸出影象，這意味著原影象上的四個畫素合併成為輸出影象中的一個畫素。實現下采樣的方法有很多種，最常見的是最大值合併、平均值合併以及隨機合併。
• 最後一個下采樣層（或卷積層）通常連線到一個或多個全連層，全連層的輸出就是最終的輸出。
• 訓練過程通過改進的反向傳播實現，將下采樣層作為考慮的因素並基於所有值來更新卷積濾波器的權重。

　　可以在這看幾個應用在 MNIST 資料集上的卷積網路的例子，在這還有一個用JavaScript實現的一個可視的類似網路。

實現

　　目前為止，我們已經學會了常見神經網路中最主要的元素了，但是我只寫了很少的在實現過程中所遇到的挑戰。

　　概括來講，我的目標是實現一個深度學習的庫，即一個基於神經網路且滿足如下條件的框架：　　　　

• • 一個可以表示多種模型的通用架構（比如所有上文提到的神經網路中的元素）
  • 可以使用多種訓練演算法（反向傳播，對比差異等等）。
  • 體面的效能

　　為了滿足這些要求，我在軟體的設計中使用了分層的思想。

結構

　　我們從如下的基礎部分開始：

• • 每個網路都包含有一個 layer 的集合。
  • 每一層中有一個 connections 的連結串列， connection 指的是兩個層之間的連線，將整個網路構成一個有向無環圖。

　　這個結構對於經典的反饋網路、RBM 及更復雜的如 ImageNet 都已經足夠靈活。

　　這個結構也允許一個 layer 成為多個網路的元素。比如，在 Deep Belief Network（深度信度網路）中的layer也可以用在其 RBM 中。

　　另外，通過這個架構可以將DBN的預訓練階段顯示為一個棧式RBM的列表，微調階段顯示為一個前饋網路，這些都非常直觀而且程式實現的很好。

資料流

下個部分介紹網路中的資料流，一個兩步過程:

1. 定義出層間的序列。例如，為了得到一個多層感知機的結果，輸入資料被賦到輸入層（因此，這也是首先被計算的層），然後再將資料通過不同的方法流向輸出層。為了在反向傳播中更新權重，輸出的誤差通過廣度優先的方法從輸出層傳回每一層。這部分通過 進行實現，應用到了網路圖結構的優勢，使用了不同的圖遍歷方法。其中一些樣例包含了 廣度優先策略 和 定位到一個指定的層。層的序列實際上由層間的連線進行決定，所以策略部分都是返回一個連線的有序列表。
2. 計算啟用值。每一層都有一個關聯的 ，包含有連線的列表（從上一步得來）和輸入值（從其它層得到）並計算得到結果的啟用值。例如，在一個簡單的S形前饋網路中，隱含層的  ConnectionCalculator 接受輸入層和偏置層的值（分別為輸入值和一個值全為1的陣列）和神經元之間的權重值（如果是全連線層，權重值實際上以一個矩陣的形式儲存在一個 FullyConnected 結構中，計算加權和，然後將結果傳給S函式。ConnectionCalculator 中實現了一些轉移函式（如加權求和、卷積）和啟用函式（如對應多層感知機的對數函式和雙曲正切函式，對應RBM的二態函式）。其中的大部分都可以通過 Aparapi 在GPU上進行計算，可以利用迷你批次訓練。

通過 Aparapi 進行 GPU 計算

　　像我之前提到的，神經網路在近些年復興的一個重要原因是其訓練的方法可以高度並行化，允許我們通過GPGPU高效的加速訓練。本文中，我選擇 Aparapi 庫來進行GPU的支援。

　　Aparapi 在連線計算上強加了一些重要的限制：

• 只允許使用原始資料型別的一維陣列（變數）。
• 在GPU上執行的程式只能呼叫 Aparapi Kernel 類本身的成員函式。

　　這樣，大部分的資料（權重、輸入和輸出資料）都要儲存在 Matrix 例項裡面，其內部是一個一維浮點陣列。所有Aparapi 連線計算都是使用 AparapiWeightedSum （應用在全連線層和加權求和函式上）、 AparapiSubsampling2D （應用在下采樣層）或 AparapiConv2D （應用在卷積層）。這些限制可以通過 Heterogeneous System Architecture　裡介紹的內容解決一些。而且Aparapi 允許相同的程式碼執行在CPU和GPU上。

訓練

　　training 的模組實現了多種訓練演算法。這個模組依賴於上文提到的兩個模組。比如，BackPropagationTrainer （所有的訓練演算法都以 Trainer 為基類）在前饋階段使用前饋層計算，在誤差傳播和權重更新時使用特殊的廣度優先層計算。

　　我最新的工作是在Java8環境下開發，其它一些更新的功能可以在這個branch 下獲得，這部分的工作很快會merge到主幹上。

結論

　　本文的目標是提供一個深度學習演算法領域的一個簡明介紹，由最基本的組成元素開始（感知機）並逐漸深入到多種當前流行且有效的架構上，比如受限波爾茲曼機。

　　神經網路的思想已經出現了很長時間，但是今天，你如果身處機器學習領域而不知道深度學習或其它相關知識是不應該的。不應該過度宣傳，但不可否認隨著GPGPU提供的計算能力、包括Geoffrey Hinton, Yoshua Bengio, Yann LeCun and Andrew Ng在內的研究學者們提出的高效演算法，這個領域已經表現出了很大的希望。現在正是最佳的時間深入這些方面的學習。

附錄：相關資源

　　如果你想更深入的學習，下面的這些資源在我的工作當中都起過重要的作用：