作者 白寧超
2015年10月15日18:30:07

摘要：程式設計師眼中的統計學系列是作者和團隊共同學習筆記的整理。首先提到統計學，很多人認為是經濟學或者數學的專利，與計算機並沒有交集。誠然在傳統學科中，其在以上學科發揮作用很大。然而隨著科學技術的發展和機器智慧的普及，統計學在機器智慧中的作用越來越重要。本系列統計學的學習基於《深入淺出統計學》一書（偏向程式碼實現，需要讀者有一定基礎，可以參見後面PPT學習）。正如（吳軍）先生在《數學之美》一書中闡述的，基於統計和數學模型對機器智慧發揮重大的作用。諸如：語音識別、詞性分析、機器翻譯等世界級的難題也是從統計中找到開啟成功之門鑰匙的。尤其是在自然語言處理方面更顯得重要，因此，對統計和數學建模的學習是尤為重要的。最後感謝團隊所有人的參與。（

)

 目錄

【程式設計師眼中的統計學（3）】概率計算：把握機會

【程式設計師眼中的統計學（11）】卡方分佈的應用

1樣本均值描述

1.1樣本均值的定義

樣本均值是我們能為總體均值做出的最好估計。在我們根據現有資訊得到的數值中，樣本均值是最有可能被作為總體均值的數值。另外樣本均值被稱為總體均值的點估計量。也就是說，作為一個基於樣本資料的計算結果，它給出了總體均值的良好估計。

1.2樣本均值符號定義和公式

這張圖顯示了樣本的分佈情況以及可以基於樣本而期望的總體分佈情況。根據已知的情況，樣本均值是我們能為總體均值做出的最好估計，所以在這我們把樣本均值稱為總體均值的點估計量。

符號（讀作"繆"）表示總體均值，為了不至於混淆，我們用（讀作"X拔"）表示樣本的均值。是的樣本對等量，它的計算方法如下：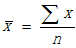

而用û（讀作"繆hat"）表示總體均值的點估計量，根據上式寫出總體的點估計量的簡明表示式，由於可以用樣本均值估計總體均值，因此：û =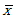

1.3樣本均值分佈演算法描述

類原始碼見源程式： predict.vo. SampleMean.java

輸入一個數組，返回樣本均值

見源程式：predict.vo. SampleMean.java

SampleMean.java 下有方法：public double run(double[] s)

呼叫封裝類：predict.utils.ScoreUtil.java

ScoreUtil.java下有方法： subZeroAndDot(String s)

package vo;
import utils.ScoreUtil;
/**
 * @(#)SampleMean.java
 * @Comments 樣本均值
 * @description 樣本均值是對總體均值的最好估計，另外樣本均值被稱為總體均值的點估計量。符號μ（讀作“繆”）表示總體均值，
 * 所以我們用“X拔”表示樣本的均值， 樣本均值等於樣本中所有資料之和除以樣本的大小。
 * @author gyz
 * @date 2015-8-15
 * @since JDK1.8
 */
public class SampleMean{
    /**
    * @param s 輸入一個數組：樣本資料
    * @return sampleMean  返回樣本均值
    * @date 2015-8-15
    * @author gyz
     */
    public  double run(double[] s) {
        double sum = 0.0;
        double sampleMean = 0.0;
        for(int i=0;i<s.length;i++){
            sum += s[i];
        }
        sampleMean = sum/s.length; 
        //並將結果保留3位小數（四捨五入）
        String fx_String = ScoreUtil.getFractionDigits(sampleMean,3);
        sampleMean = Double.valueOf(fx_String);
        System.out.println("樣本均值："+sampleMean);    
        return sampleMean ;
   }
}

1.4樣本均值使用場景

當資料或事件數量十分龐大時，很難決定從何處著手收集資料，我們就可以有效地、正確地採用抽樣收集資料。我們可以使用樣本均值估計資料的總體均值。

1.5樣本均值優缺點

1.5.1樣本均值優點

可以樣本資料的均值估計總體均值，可以由此得知總體方差的期望形態。

1.5.2. 樣本均值缺點

通過樣本均值估計總體均值不一定是非常正確的，也會存在一些誤差，或者需要在進行一些驗證等。

1.6 樣本均值演算法的輸入資料

* @param s 輸入一個數組：樣本資料

1.7樣本均值演算法的輸出結果

* @return sampleMean 返回樣本均值

1.8樣本均值演算法異常和誤差

1.8.1樣本均值演算法可能異常或誤差

異常：輸入資料不合法；

誤差：保留小數位數造成不精確

1.8.2樣本均值演算法異常或誤差處理

異常：解決，輸入不合法給予提示。

誤差：解決，進行小數點位數自定義保留封裝，根據具體精度進行設定。

2估計總體方差的相關描述

2.1 估計總體方差的定義

     一個數據集的方差所量度的是數值與均值的偏離程度。當你選擇一個樣本後，相比總體，你擁有的數值數量變少了，因此，與總體的數值偏離均值的程度相比，樣本中的數值更有可能以緊密的方式聚集在均值周圍，也就是說，極端數值出現在樣本中的可能性下降，這是因為總的來說這樣的數值變小了。所以樣本資料的方差可能不是總體方差的最好估計辦法。我們需要找到一個更好的辦法來估計總體方差，也就是說，找到樣本資料的某個函式，而這個函式所得出的結果要稍微大於所有樣本數值的方差。

2.2估計總體方差符號定義和公式

符號 表示總體方差，所以我們用一個略有變化的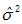表示總體方差的點估計量，n為樣本的大小，估計總體方差計算公式如下：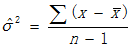

總體方差點估計量的式子通常寫作,由此得到：=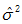

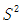
2.3總體方差和估計總體方差的使用場景

    如果想求確切的總體方差，且擁有全部總體資料n，總體均值為，則可以使用下式計算：

如果需要求樣本資料估計總體方差，則需要用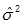公式，除數為n-1。

2.4樣本均值分佈演算法描述

類原始碼見源程式： predict.vo. EstimateGeneralityVariance.java

輸入一個樣本資料的陣列，返回估計總體方差值

見源程式：predict.vo. EstimateGeneralityVariance.java

SampleMean.java 下有方法：public double run(double[] s)

呼叫封裝類：predict.utils.ScoreUtil.java

ScoreUtil.java下有方法： subZeroAndDot(String s)

package vo;

import utils.ScoreUtil;
/**
 * @(#)EstimateGeneralityVariance.java
 * @Comments 估計總體方差
 * @description 符號σ^2 表示總體方差，估計總體方差等於樣本中的每一個數值減去樣本均值，所得之差取平方和數，
 * 然後將所有平方和相加，再除以樣本大小n減1。
 * @author gyz
 * @date 2015-8-15
 * @since JDK1.8
 */
public class EstimateGeneralityVariance {
    /**
     * 
     * @param s 輸入一個數組：樣本資料
     * @return egv 返回估計總體方差值
     */
    public  double run(double[] s) {
        SampleMean sm = new SampleMean();
        double sampleMean = sm.run(s);
        double different= 0.0;
        double egv;
        int n = s.length;
        for(int i=0;i<n;i++){
            different = (s[i]- sampleMean)*(s[i]- sampleMean);
        }
        egv = different/(n-1);
        //並將結果保留3位小數（四捨五入）
        String fx_String = ScoreUtil.getFractionDigits(egv,3);
        egv = Double.valueOf(fx_String);
        System.out.println("估計總體方差值："+egv);    
        return egv ;
   }
}

2.5估計總體方差使用場景

    當資料或事件數量十分龐大時，很難決定從何處著手收集資料，我們就可以有效地、正確地採用抽樣收集資料。我們可以使用樣本資料估計資料的總體方差。

2.6估計總體方差優缺點

2.6.1估計總體方差優點

我麼使用樣本資料估計總體方差，可以由此得知總體樣本的期望形態。

2.6.2. 估計總體方差缺點

通過使用樣本資料估計總體方差不一定是非常正確的，也會存在一些誤差，或者需要在進行一些驗證等。

2.7 估計總體方差演算法的輸入資料

* @param s 輸入一個數組：樣本資料

2.8樣本均值演算法的輸出結果

* @return egv 返回估計總方差值

2.9樣本均值演算法異常和誤差

2.9.1樣本均值演算法可能異常或誤差

異常：輸入資料不合法；

誤差：保留小數位數造成不精確

2.9.2樣本均值演算法異常或誤差處理

異常：解決，輸入不合法給予提示。

誤差：解決，進行小數點位數自定義保留封裝，根據具體精度進行設定。

3比例的抽樣分佈描述

3.1比例抽樣分佈的定義

    如果從一個總體中用相同的方法抽取許多大小相同但存在差異的樣本，然後用每個樣本的某個屬性形成一個分佈，所得結果稱為抽樣分佈。由此得出，用每個樣本的比例形成的抽樣分佈就是"比例抽樣分佈"。比例抽樣分佈是一種概率分佈，由所有大小為n的可能樣本的各種比例構成。如果我們知道這些比例的分佈，就能用這個分佈求出某一個特定樣本的比例的發生概率。

3.2比例抽樣分佈符號定義

    已知總體中紅色糖球的比例，用p（proportion）表示，每一大盒糖球其實就是從糖球總體中取出的一個樣本。樣本的大小用n來表示。如果隨機變數X代表樣本中的紅色糖球的數目，則X~B(n,p)。樣本中的紅色糖球的比例取決於X（樣本中的紅色糖球的數目），即比例本身是一個隨機變數，用P_s 表示，且P_s =X/n。可以取出大小為n的所有可能樣本，每一個可能樣本會包含n顆糖球，每一盒樣本中紅色糖球的數量會符合相同的分佈。利用所有可能的樣本，我們能得出所有樣本比例的分佈，該分佈稱作"比例抽樣分佈"，或者稱作" P_s 的分佈"。

3.3比例抽樣分佈計算步驟

1 檢視與我們的特定樣本大小相同的所有樣本。

如果我們有一個大小為n的樣本，就要考慮所有大小為n可能樣本，在本例中，盒子的糖球數量為100，因此n為100。

2 觀察所有樣本形成的分佈，然後求出比例的期望和方差。

每一樣本都有自己的情況，因此每一個包裝盒裡的紅色糖球的比例都有可能發生變化。我們用隨機變數X代表樣本中的紅色糖球的數目，則X~B(n,p)，其中n=100,p=0,25。樣本中紅色糖球的比例取決於X（樣本中紅色糖球的資料），即比例本身是一個隨機變數，可以將此記為Ps , P_s = X/n。所以P_s 的期望和方差分別如下： E(P_s) = p   和  Var(P_s) =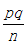

3 得出上述比例的分佈後，利用該分佈求出概率。

當n很大時，Ps的分佈接近正態分佈。即當n>30的時候，Ps符合正態分佈，利用正態分佈解答我們的概率問題。但是每個樣本都是離散的，因此在計算概率時，需要進行連續性修正。P_s 的正態分佈如下：

3.4比例抽樣分佈使用場景

 當資料或事件數量十分龐大時，很難決定從何處著手收集資料，我們就可以有效地、正確地採用抽樣收集資料。從一個已知總體中取出某個樣本的比例的時候，需要得知樣本的期望形態，即可使用比例抽樣分佈。

3.5比例抽樣分佈優缺點

1. 比例抽樣分佈優點 ：可以使用比例的抽樣分佈求出從一個已知總體中取出的某個樣本的比例的概率，可以由此得知樣本的期望形態。
2. 比例抽樣分佈缺點 ：通過比例抽樣分佈得出的樣本的期望不一定是非常正確的，也會存在一些誤差，或者需要在進行一些驗證等。

3.6 比例抽樣分佈演算法的輸入資料

* @param n 樣本大小

* @param p 總體中某一類的所佔比例

* @param x 你所要求比例抽樣分佈概率的隨機變數

3.7比例抽樣分佈演算法的輸出結果

輸出中間結果

* @return E(Ps) 比例抽樣分佈的期望E(Ps)

* @return Var(Ps) 比例抽樣分佈的方差Var(Ps)

輸出最終結果

* @return 小於或等於符合正態分佈的隨機變數X的概率值

3.8比例抽樣分佈演算法異常和誤差

3.8.1比例抽樣分佈演算法可能異常或誤差

異常：輸入資料不合法

誤差：保留小數位數造成不精確

3.8.2比例抽樣分佈概率演算法異常或誤差處理

異常：解決，輸入不合法給予提示。

誤差：解決，進行小數點位數自定義保留封裝，根據具體精度進行設定

3.9比例抽樣分佈演算法描述

類原始碼見源程式： predict.vo.ProportionSampleDistribution.java

方法描述

通過對需要計算比例抽樣分佈的均值和標準差進行計算得出具體標準分再通過呼叫org.apache.commons.math3.distribution類來實現。

類原始碼見源程式：predict.vo.ProportionSampleDistribution.java

ProportionSampleDistribution.java 下有如下方法：

public static double calculateExpectedValue(int n,double p)

//比例抽樣分佈的期望

public static double calculateVariance(int n,double p)

//比例抽樣分佈的方差

cumulativeProbability(double z)

//需要求符合正態分佈的比例抽樣分佈的標準分。

呼叫封裝方法：

predict.utils.ScoreUtil.java 下有如下方法：subZeroAndDot(String s)

//對傳入的數保留3位小數

package vo;
import org.apache.commons.math3.distribution.NormalDistribution;
import utils.ScoreUtil;

/**
 * @(#)ProportionSampleDistribution.java
 * @Comments  比例抽樣分佈（求期望和方差）
 * @description 樣本中某一類的數目X符合二項分佈B(n,p),樣本中某一類所佔的比例是一個隨機變數,記為Ps,且Ps=X/n
 * @author gyz
 * @date 2015-8-15
   @since   JDK1.8  
 */
public class ProportionSampleDistribution {
     /**
      * 計算比例抽樣分佈的期望
      * @param n 樣本大小
      * @param p 總體中某一類的所佔比例
      * @return 比例抽樣分佈的期望E(Ps)=E(X/n)=E(X)/n
      */
    public static double calculateExpectedValue(int n,double p){
        //計算二項分佈B(n,p)的期望
        double bEx = n*p; 
        //利用總體期望求樣本期望:E(Ps)=E(X/n)=E(X)/n
        double EPs = bEx/n;
        //並將結果保留3位小數（四捨五入）
        String EPs_String = ScoreUtil.getFractionDigits(EPs, 3);
        EPs = Double.valueOf(EPs_String);
        System.out.println("比例抽樣分佈的期望："+EPs);
        return EPs;
    }
     /**
     * 計算比例抽樣分佈的方差
     * @param n 樣本大小
     * @param p 總體中某一類的所佔比例
     * @return 比例抽樣分佈的方差Var(Ps)=Var(X/n)=Var(X)/n2
     */
    public static double calculateVariance(int n,double p){
        
        //計算二項分佈B(n,p)的方差[公式：Var(X)=npq]
        double bVar = n*p*(1-p); 
        //利用總體方差求樣本方差:var(Ps)=var(X/n)=var(X)/n
        double VarPs = bVar/n*n;
        
        //並將結果保留3位小數（四捨五入）
        String VarPs_String = ScoreUtil.getFractionDigits(VarPs, 3);
        VarPs = Double.valueOf(VarPs_String);
        System.out.println("比例抽樣分佈的方差："+VarPs);
        return VarPs;
    }        
    /**
     * @param args
     */
    public static void run(int n,double p,double x) {
        NormalDistribution normalDistributioin = new NormalDistribution(0,1);
        double u = calculateExpectedValue(n,p);
        double σ2 = calculateVariance(n,p);
        //normalDistribution(x);
        double σ = Math.sqrt(σ2);
        double z = (x-u)/σ;
        double fx = normalDistributioin.cumulativeProbability(z);
         //並將結果保留3位小數（四捨五入）
         String fx_String = ScoreUtil.getFractionDigits(fx,3);
         fx = Double.valueOf(fx_String);
         System.out.println("比例抽樣分佈X的概率："+fx);         
    }
}

4均值的抽樣分佈

4.1均值抽樣分佈的定義

    如果從一個總體中用相同的方法抽取許多大小相同但存在差異的樣本，然後用每個樣本的某個屬性形成一個分佈，所得結果稱為抽樣分佈。由此得出，用每個樣本的均值形成的抽樣分佈就是"均值抽樣分佈"。均值抽樣分佈是一種概率分佈，由所有大小為n的可能樣本的均值構成。如果我們知道這些樣本均值的分佈，就能用這個分佈求出某一個特定樣本均值的發生概率。

4.2均值抽樣分佈符號定義

    已知總體的均值和方差，並用和表示，一個包裝袋中的糖球數量可以用X表示。隨機選擇的每一袋糖球都是X的一個獨立觀察結果，如果用代表隨機選擇的一袋糖球中的糖球數量，則每個的期望都是u，方差為。我們可以用表示這n袋糖球的容量均值，計算如下：

現在我們取出大小為n的所有可能樣本，每一個可能樣本包含n袋糖球，即每一個樣本都包含X的n個獨立觀察結果。利用所有可能的樣本，我們利用從所有可能樣本得出的形成一個分佈，該分佈稱作"均值抽樣分佈"，或者稱作"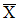的分佈"。

4.3均值抽樣分佈計算步驟

1 檢視與我們的特定樣本大小相同的所有樣本。

如果我們有樣本大小為n，就要考慮所有大小為n可能樣本，在本例中，小包裝糖球有30袋，因此n為30。

2 觀察所有樣本形成的分佈，然後求出樣本均值的期望和方差。

每一樣本都各有特點，每個包裝袋中的糖球數目有變化。已知總體的均值和方差，並用和表示，一個包裝袋中的糖球數量可以用X表示。隨機選擇的每一袋糖球都是X的一個獨立觀察結果，如果用代表隨機選擇的一袋糖球中的糖球數量，則每個的期望都是u，方差為。我們用表示這n袋糖球的容量均值。這裡的每一個Xi都是X的一個獨立觀察值，且我們已知E(X) = u，Var(X)=。所以的期望和方差分別如下： E(x) = u 和Var(x) =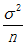

3 得出上述樣本均值的分佈後，利用該分佈求出概率。

只要知道所有可能樣本的均值的分佈情況，就能利用該分佈求出一個隨機樣本的均值的概率，在本例中，隨機樣本即小包裝糖球。當n很大時，的分佈接近正態分佈。當X符合正態分佈，則符合正態分佈；當X不符合正態分佈，但是當n>30的時候，仍然符合正態分佈。

4.4均值抽樣分佈使用場景

 當資料或事件數量十分龐大時，很難決定從何處著手收集資料，我們就可以有效地、正確地採用抽樣收集資料。從一個已知總體中取出某個樣本的均值的時候，需要得知樣本的期望形態，即可使用均值抽樣分佈。

4.5均值抽樣分佈優缺點

4.5.1均值抽樣分佈優點

可以使用均值的抽樣分佈求出從一個已知總體中取出的某個樣本的均值的概率，可以由此得知樣本的期望形態。

4.5.2.均值抽樣分佈缺點

通過均值抽樣分佈得出的樣本的期望不一定是非常正確的，也會存在一些誤差，或者需要在進行一些驗證等。

4.6 均值抽樣分佈演算法的輸入資料

* @param s 輸入一個數組：樣本資料

* @param x 你所要求均值抽樣分佈概率的隨機變數

4.7比例抽樣分佈演算法的輸出結果

輸出中間結果

* @return E(mean) 均值抽樣分佈的期望

* @return Var(mean) 均值抽樣分佈的方差

輸出最終結果

* @return 小於或等於符合正態分佈的隨機變數X的概率值

4.8均值抽樣分佈演算法異常和誤差

4.8.1均值抽樣分佈演算法可能異常或誤差

異常：輸入資料不合法；當n小於或等於30時，丟擲異常，不能使用正態分佈計算概率。

誤差：保留小數位數造成不精確

4.8.2均值抽樣分佈演算法異常或誤差處理

異常：解決，輸入不合法給予提示。

誤差：解決，進行小數點位數自定義保留封裝，根據具體精度進行設定

4.9均值抽樣分佈演算法描述

類原始碼見源程式： predict.vo.MeanSampleDistributio

方法描述

通過對需要計算均值抽樣分佈的均值和標準差進行計算得出具體標準分再通過呼叫org.apache.commons.math3.distribution類來實現。。

類原始碼見源程式：predict.vo.MeanSampleDistribution.java

MeanSampleDistribution.java 下有如下方法：

public static double calculateExpectedValue(double[] s)

//均值抽樣分佈的期望

public static double calculateVariance(double[] s)

//均值抽樣分佈的方差

cumulativeProbability(double z)

//需要求符合正態分佈的比例抽樣分佈的標準分。

呼叫封裝類：

predict.utils.ScoreUtil.java 下有如下方法：subZeroAndDot(String s)

package vo;
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;

import org.apache.commons.math3.distribution.NormalDistribution;

import utils.ScoreUtil;

/**
 * @(#)MeanSampleDistribution.java
 * @Comments  均值抽樣分佈（求期望和方差）
 * @description
 *     1.我們抽取總體中的大小為n的所有可能樣本，可以標記為S1,S2,,,Sn，然後用這些樣本的均值形成一個分佈。
 *  2.S1=[X1,X2,,,Xn] S2=[X1,X2,,,Xn],,,Sn=[X1,X2,,,Xn] 由於每一個Xi都是X的一個獨立觀察結果。所以每個Xi
 *    的期望都是u，方差都是σ^2。
 *  3.E(X)=u,var(X)=σ^2， 樣本均值mean=(X1+X2+...+Xn)/n
 * @author gyz
 * @date 2015-8-15
   @since   JDK1.8 
 */
public class MeanSampleDistribution {

    /**
     * 計算均值抽樣分佈的期望
     * @param s 輸入一個數組：樣本資料
     * @return 均值抽樣分佈的期望E(mean)=E((X1+X2+....+Xn)/n)=(E(X1)+E(X2)+...+E(Xn))/n
     */
    public static double calculateExpectedValue(double[] s){
        
        //計算樣本均值
        int sum=0;
        for(int i=0;i<s.length;i++){
            sum += s[i];
        }
        double mean = sum*1.0/s.length;
        //求均值抽樣分佈的期望
        double Emean;
        Emean = mean;
        
        //並將結果保留3位小數（四捨五入）
        String Emean_string = ScoreUtil.getFractionDigits(Emean, 3);
        Emean = Double.valueOf(Emean_string);
        System.out.println("均值抽樣分佈的期望："+Emean);
        return Emean;
    }
    
     /**
    * 計算均值抽樣分佈的方差
    * @param s 輸入一個數組：樣本資料
    * @return 比例抽樣分佈的方差var(mean)=var((X1+X2+....+Xn)/n)=(var(X1)+var(X2)+...+var(Xn))/n
    */
    public static double calculateVariance(double[] s){
        //求均值抽樣分佈的方差
        int sum = 0;
        int n = s.length;
        double Varmean=0.0; 
        for(int i=0;i<n;i++){
            sum += s[i];
        }
        double mean = sum*1.0/n;
        for(int i=0;i<n;i++){
            Varmean += (s[i] - mean)*(s[i] - mean);
        }
        Varmean = Varmean/n; 
        //並將結果保留3位小數（四捨五入）
        String Varmean_string = ScoreUtil.getFractionDigits(Varmean, 2);
        Varmean = Double.valueOf(Varmean_string);
        System.out.println("均值抽樣分佈的方差："+Varmean);
        return Varmean;
    }
    /**
     * @param args
     * @return 
     */
    public static void run(double[] t,double x) {
        NormalDistribution normalDistributioin = new NormalDistribution(0,1);

        double u = calculateExpectedValue(t);
        double σ2 = calculateVariance(t);
        double σ = Math.sqrt(σ2);
        double z = (x-u)/σ;
        double fx = normalDistributioin.cumulativeProbability(z); 
        //並將結果保留3位小數（四捨五入）
        String fx_String = ScoreUtil.getFractionDigits(fx,3);
        fx = Double.valueOf(fx_String);
        System.out.println("均值抽樣分佈X的概率："+fx);    
    }

}

5 中心極限定理的使用

6 總結與共享

6.1 總結

6.2共享