做一個豁達而努力的自己。

漢諾塔問題是一個典型的遞迴問題，其實也就是按照自己思路寫出來就行了，，，

有3柱塔A，B，C，A為初始塔，B為藉助塔，C為目標塔，，，

目標是要將A上的圓盤藉助B運到C，

規則：1.每次只能移動一個圓盤，

          2.圓盤可以放到A，B，C中任意一個塔上，

          3.任意時刻不可以將較大圓盤放在較小圓盤上面，

分析（藉助程式碼）：

    當A上只有1個圓盤時，直接可以將圓盤運到C，

    當A上有2個圓盤時，先將1號（最上面的小的）圓盤運到B上，再將2號圓盤運到C上，再將1號圓盤從B運到C上，

    當A上有3個圓盤時，先將1，2號圓盤運到B上，再將3號圓盤運到C上，再將1，2號圓盤從B運到C上，

    當A上有n個圓盤時，先將n-1個圓盤運到B上，再將n號圓盤運到C上，再將n-1個圓盤從B運到C上，

其實也就是按著這個思想，寫函式就可以了，，，

程式碼：

#include <iostream>
using namespace std;

void move(int n, char a, char c)
{
    cout << n << " " << a << " -> " << c << endl;;
}
void Hannuota(int n, char a, char b, char c)
{
    if(n == 1)  //當A中只有一個圓盤時，將1號盤從A移動到C上
        move(1, a, c);
    else
    {
        Hannuota(n - 1, a, c, b);   //將n-1個圓盤從A藉助C移動到B上
        move(n, a, c);  //將最後的n號盤從A移動到C上
        Hannuota(n - 1, b, a, c);   //再將n-1個盤從B藉助A移動到C上
    }
}
int main()
{
    char a = 'A', b = 'B', c = 'C';
    int n;
    cout << "輸入A塔上圓盤的個數:";
    cin >> n;
    Hannuota(n, a, b, c);
    return 0;
}
 

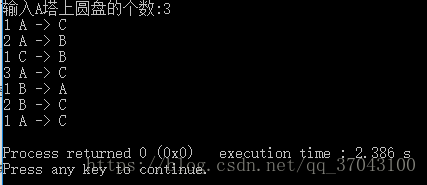
執行結果：