最近在看關於Matting的文章，這篇論文算是比較經典的老論文了，所以翻譯過來，閱讀更加方便些。

文章翻譯大部使用谷歌線上翻譯，對其中小部分錯誤進行了修正。

A Bayesian Approach to Digital Matting

1、Introduction

In digital matting, a foreground element is extracted from a background image by estimating a color and opacity for the foreground element at each pixel.

通過估計每個畫素處的前景元素的顏色和不透明度，從背景影象中提取前景元素。

The opacity value at each pixel is typically called its alpha (0~1)

Matting is used in order to composite the foreground element into a new scene.

使用融合(Matting)來將前景元素合成為新場景。

2、Background

the alpha channel—and showed how synthetic images with alpha could be useful in creating complex digital images. The most common compositing operation is the over operation, which is summarized by the compositing equation:

alpha通道展示了具有alpha的合成影象如何在建立複雜的數字影象時有用。最常見的合成操作是過操作，其由合成方程是：

where C, F, and B are the pixel’s composite, foreground, and background colors, respectively, and α is the pixel’s opacity component used to linearly blend between foreground and background.

其中C，F和B分別是畫素的合成，前景和背景顏色，α是用於在前景和背景之間線性組合的畫素不透明度元件。

Blue screen matting was among the first techniques used for live action matting. The principle is to photograph the subject against a constant-colored background, and extract foreground and alpha treating each frame in isolation. This single image approach is underconstrained since, at each pixel, we have three observations and four unknowns. Vlahos pioneered the notion of adding simple constraints to make the problem tractable; this work is nicely summarized by Smith

藍屏消光是用於真人動作消光的首批技術之一。原理是在恆定顏色的背景下拍攝物件，並提取前景和alpha處理每個幀。這種單一影象方法不受約束，因為在每個畫素處，我們有三個觀察值和四個未知數。Vlahos開創了新增簡單約束以使問題易於處理的概念; Smith & Blinn [Blue Screen Matting]很好地總結了這項工作。

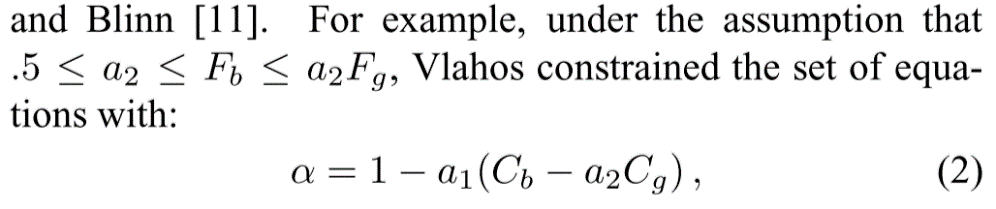
Where and $c_{g}$ are the blue and green channels of the input image,

其中$c_{b}$和$c_{g}$是輸入影象的blue和green通道

respectively, and a1 and a2 are user-controlled tuning parameters. Additional constraint equations such as this one, however, while easy to implement, are ad hoc, require an expert to tune them, and can fail on fairly simple foregrounds.

$a_{1}和$a_{2}分別是使用者控制的調諧引數。然而，諸如此類的附加約束方程雖然易於實現，但這是臨時的，需要人來調整它們，並且有可能在很簡單的前景的情境下出現錯誤。

More recently, Mishima [5] developed a blue screen matting technique based on representative foreground and background samples. In particular, the algorithm starts with two identical polyhedral (triangular mesh) approximations ofa sphere in rgb space centered at the average value B of the background samples.

最近，Mishima [5]開發了一種基於代表性前景和背景樣本的藍屏消光技術。特別地，該演算法通過RGB空間以背景樣本B之平均值為中心的兩個相同的多面體（三角形網路）近似開始

The vertices of one of the polyhedra (the background polyhedron) are then repositioned by moving them along lines radiating from the center until the polyhedron is as small as possible while still containing all the background samples. The vertices of the other polyhedron (the foreground polyhedron) are similarly adjusted to give the largest possible polyhedron that contains no foreground pixels from the sample provided. Given a new composite color C, then, Mishima casts a ray from B through C and defines the intersections with the background and foreground polyhedra to be B and F, respectively. The fractional position of C along the line segment BF is α.

然後通過沿著從中心輻射的線移動多面體的一個頂點（背景多面體）來重新定位，直到多面體儘可能小，同時仍然包含所有背景樣本。類似地調整另一個多面體（前景多面體）的頂點以給出最大可能的多面體，其不包含來自所提供的樣本的前景畫素。給定一個新的複合顏色C，然後，Mishima投射從B到C的光線，並將背景和前景多面體的交點分別定義為B和F. 沿著線段BF的C的分數位置是α。

Under some circumstances, it might be possible to photograph a foreground object against a known but non-constant background. One simple approach for handling such a scene is to take a difference between the photograph and the known background and determine α to be 0 or 1 based on an arbitrary threshold. This approach, known as difference matting [9] is error prone and leads to “jagged” mattes. Smoothing such mattes by blurring can help with the jaggedness but does not generally compensate for gross errors.

在某些情況下，它可以針對已知但非恆定的背景拍攝前景物件。處理這種場景的一種簡單方法是在照片和已知背景之間取差異，並基於任意閾值確定α為0或1。這種被稱為差異消光的方法（參見例如[9]）容易出錯並導致“鋸齒狀”融合。通過模糊來平滑這些融合能夠有助於減少鋸齒狀，但通常不能彌補嚴重錯誤。

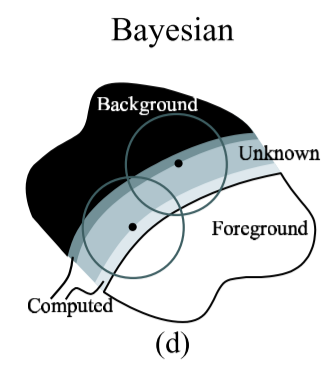
One limitation of blue screen and difference matting is the reliance on a controlled environment or imaging scenario that provides a known, possibly constant-colored background. The more general problem of extracting foreground and alpha from relatively arbitrary photographs or video streams is known as natural image matting. To our knowledge, the two most successful natural image matting systems are Knockout, developed by Ultimatte (and, to the best ofour knowledge, described in patents by Berman et al. [1, 2]), and the technique of Ruzon and Tomasi [10]. In both cases, the process begins by having a user segment the image into three regions: definitely foreground, definitely background, and unknown (as illustrated in Figure 1(a)). The algorithms then estimate F,B, and α for all pixels in the unknown region.

藍屏和差異消光的一個限制是依賴於受控環境或成像場景，其提供已知的，可能是恆定顏色的背景。從相對任意的照片或視訊中提取前景和alpha的更一般的問題被稱為自然影象消光。據我們所知，兩個最成功的自然影象消光系統是由Ultimatte開發的Knockout（以及Berman等[1,2]專利中描述的最佳知識），以及Ruzon和Tomasi的技術[10]。在這兩種情況下，該過程首先讓使用者將影象分成三個區域：絕對前景，明確背景和未知（如圖a所示）。 然後演算法估計未知區域中所有畫素的F，B和α。

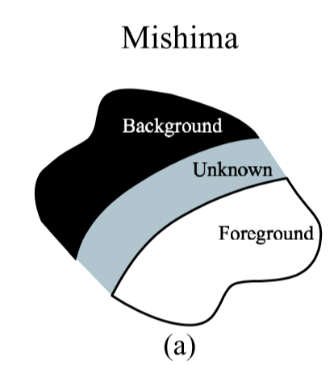
For Knockout, after user segmentation, the next step is to extrapolate the known foreground and background colors into the unknown region. In particular, given a point in the unknown region, the foreground F is calculated as a weighted. sum of the pixels on the perimeter of the known foreground region. The weight for the nearest known pixel is set to 1, and this weight tapers linearly with distance, reaching 0 for pixels that are twice as distant as the nearest pixel. The same procedure is used for initially estimating the background B based on nearby known background pixels. Figure 1(b) shows a set of pixels that contribute to the calculation of F and B of an unknown pixel.

對於Knockout，在使用者分割之後，下一步是將已知的前景色和背景色外推到未知區域。特別地，給定未知區域中的點，前景F被計算為加權。已知前景區域周邊上的畫素之和。最近的已知畫素的權重設定為1，並且該權重隨距離線性地逐漸變細，對於距離最近畫素兩倍的畫素，該權重達到0。基於附近的已知背景畫素，使用相同的過程來初始估計背景B. 圖b顯示了一組有助於計算未知畫素的F和B的畫素。

The estimated background color B is then refined to give B using one of several methods [2] that are all similar in character. One such method establishes a plane through the estimated background color with normal parallel to the line BF. The pixel color in the unknown region is then projected along the direction of the normal onto the plane, and this projection becomes the refined guess for B. Figure 1(f) illustrates this procedure.

然後將估計的背景顏色B細化以使用幾種在性質上相似的方法[2]中的一種來給出B. 一種這樣的方法通過估計的背景顏色建立平面，其中法線平行於線B`F。然後將未知區域中的畫素顏色沿法線方向投影到平面上，並且該投影成為B的精確猜測。圖f示出了該過程。

最後，Knockout根據公式估計α

where f(·) projects a color onto one of several possible axes through rgb space (e.g., onto one of the r-, g-, or b- axes). Figure 1(f) illustrates alphas computed with respect to the r- axes and g- axes. In general, α is computed by projection onto all of the chosen axes, and the final α is taken as a weighted sum over all the projections, where the weights are proportional to the denominator in equation (3) for each axis.

其中f(·)通過RGB空間（例如，在r軸，g軸或b軸之上）將顏色投影到幾個可能的軸之上。圖f示出了相對於r軸和g軸計算的α。通常，α通過投影到所有選定軸上來計算，並且最終α被視為所有投影的加權和，其中權重與等式（3）中的每個軸的分母成比例。

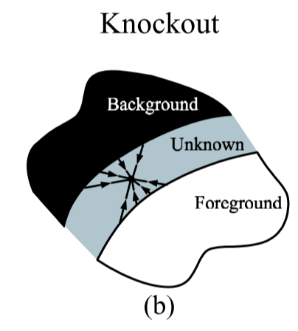
Ruzon and Tomasi [10] take a probabilistic view that is somewhat closer to our own. First, they partition the unknown boundary region into sub-regions. For each sub-region, they construct a box that encompasses the sub-region and includes some of the nearby known foreground and background regions (see Figure 1(c)). The encompassed foreground and background pixels are then treated as samples from distributions P(F) and P(B), respectively, in color space. The foreground pixels are split into coherent clusters, and unoriented Gaussians (i.e., Gaussians that are axis-aligned in color space) are fit to each cluster, each with mean F and diagonal covariance matrix ΣF. In the end, the foreground distribution is treated as a mixture (sum) of Gaussians. The same procedure is performed on the background pixels yielding Gaussians, each with mean B and covariance ΣB, and then every foreground cluster is paired with every background cluster. Many of these pairings are rejected based on various “intersection” and “angle” criteria. Figure 1(g) shows a single pairing for a foreground and background distribution.

Ruzon和Tomasi [10]採用的概率觀點更接近我們的方法。首先，它們將未知邊界區域劃分為子區域。對於每個子區域，它們構造一個包含子區域的框，幷包括一些附近已知的前景區域和背景區域（參見圖c）。然後將包圍的前景和背景畫素分別作為來自顏色空間中的分佈P(F)和P(B)的樣本處理。前景畫素被分成相干簇，並且未定向高斯（即，在顏色空間中軸對齊的高斯）適合於每個簇，每個簇具有平均F和對角線協方差矩陣ΣF。最後，前景分佈被視為高斯的混合（和）。對產生高斯的背景畫素執行相同的過程，每個高斯具有均值B和協方差ΣB，然後每個前景聚類與每個背景聚類配對。基於各種“交叉”和“角度”標準，許多這些配對被拒絕。圖1（g）顯示了前景和背景分佈的單個配對。

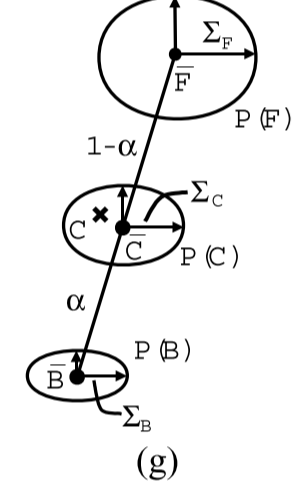
After building this network of paired Gaussians, Ruzon and Tomasi treat the observed color C as coming from an intermediate distribution P(C), somewhere between the foreground and background distributions. The intermediate distribution is also defined to be a sum ofGaussians, where each Gaussian is centered at a distinct mean value C located fractionally (according to a given alpha) along a line between the mean of each foreground and background cluster pair with fractionally interpolated covariance ΣC, as depicted in Figure 1(g). The optimal alpha is the one that yields an intermediate distribution for which the observed color has maximum probability; i.e., the optimal α is chosen independently of F and B. As a post-process, the F and B are computed as weighted sums of the foreground and background cluster means using the individual pairwise distribution probabilities as weights. The F and B colors are then perturbed to force them to be endpoints of a line segment passing through the observed color and satisfying the compositing equation.

在構建成對高斯的這個網路之後，Ruzon和Tomasi將觀察到的顏色C視為來自中間分佈P(C)，介於前景和背景分佈之間。中間分佈也被定義為高斯函式的和，其中每個高斯中心位於沿著每個前景和背景聚類對的平均值之間的線小數（根據給定的α）定位的不同平均值C，具有分數插值協方差ΣC ，如圖g所示。最佳α是產生中間分佈的α，其中觀察到的顏色具有最大概率;即，最優α獨立於F和B選擇，作為後處理。F和B被計算為前景和背景聚類均值的加權和，使用各個成對分佈概率作為權重。然後擾動F和B顏色以迫使它們成為穿過觀察到的顏色並滿足合成方程的線段的端點。

Both the Knockout and the Ruzon-Tomasi techniques can be extended to video by hand-segmenting each frame, but more automatic techniques are desirable for video. Mitsunaga et al. [6] developed the AutoKey system for extracting foreground and alpha mattes from video, in which a user seeds a frame with foreground and background contours, which then evolve over time. This approach, however, makes strong smoothness assumptions about the foreground and background (in fact, the extracted foreground layer is assumed to be constant near the silhouette) and is designed for use with fairly hard edges in the transition from foreground to background; i.e., it is not well-suited for transparency and hair-like silhouettes.

Knockout和Ruzon-Tomasi技術都可以通過手動分割每個幀擴充套件到視訊，但視訊需要更多的自動技術。Mitsunaga等人[6]開發了AutoKey系統，用於從視訊中提取前景和alpha融合，其中使用者播種具有前景和背景輪廓的幀，然後隨著時間的推移進化。然而，這種方法對前景和背景做出了很強的平滑假設（事實上，假設提取的前景層在輪廓附近是恆定的），並且設計用於從前景到背景的過渡中相當硬的邊緣; 即，它不適合透明度和頭髮般的輪廓。

In each of the cases above, a single observation of a pixel yields an underconstrained system that is solved by building spatial distributions or maintaining temporal coherence. Wallace [12] provided an alternative solution that was independently (and much later) developed and refined by Smith and Blinn [11]: take an image of the same object in front of multiple known backgrounds. This approach leads to an overconstrained system without building any neighborhood distributions and can be solved in a least-squares framework. While this approach requires even more controlled studio conditions than the single solid background used in blue screen matting and is not immediately suitable for live-action capture, it does provide a means ofestimating highly accurate foreground and alpha values for real objects. We use this method to provide ground-truth mattes when making comparisons.

在上述每種情況下，對畫素的單次觀察產生通過構建求解的欠約束系統空間分佈或保持時間一致性。Wallace[12]提供了另一種解決方案，由Smith & Blinn [11]獨立（後來）開發和完善：在多個已知背景前拍攝同一物體的影象。這種方法導致過度約束系統而不構建任何鄰域分佈，並且可以在最小二乘框架中求解。雖然這種方法需要比藍屏遮中使用的單一實體背景更加受控制的工作室條件，並且不能立即適用於實時捕捉，但它確實提供了一種估算真實物體的高精度前景和alpha值的方法。我們使用這種方法在進行比較時提供ground-truth融合。

3、Our Bayesian framework

For the development that follows, we will assume that our input image has already been segmented into three regions: “background,” “foreground,” and “unknown,” with the background and foreground regions having been delineated conservatively. The goal of our algorithm, then, is to solve for the foreground color F, background color B, and opacity α given the observed color C for each pixel within the unknown region of the image. Since F, B, and C have three color channels each, we have a problem with three equations and seven unknowns.

對於隨後的開發，我們將假設我們的輸入影象已經被分割成三個區域：“背景”，“前景”和“未知”，其中背景和前景區域已經保守地描繪。然後，我們的演算法的目標是在給定影象的未知區域內的每個畫素的觀察到的顏色C的情況下求解前景色F，背景色B和不透明度α。由於F，B和C各有三個顏色通道，因此我們遇到三個方程和七個未知數的問題。

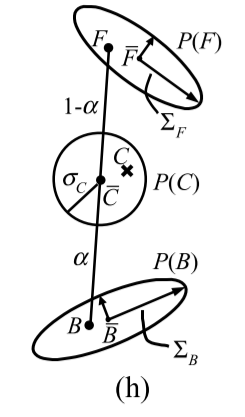
Like Ruzon and Tomasi [10], we will solve the problem in part by building foreground and background probability distributions from a given neighborhood. Our method, however, uses a continuously sliding window for neighborhood definitions, marches inward from the foreground and background regions, and utilizes nearby computed F, B, and α values (in addition to these values from “known” regions) in constructing oriented Gaussian distributions, as illustrated in Figure 1(d). Further, our approach formulates the problem of computing matte parameters in a well-defined Bayesian framework and solves it using the maximum a posteriori (MAP) technique. In this section, we describe our Bayesian framework in detail.

像Ruzon和Tomasi [10]一樣，我們將通過構建來自給定鄰域的前景和背景概率分佈來解決問題。然而，我們的方法使用連續滑動視窗進行鄰域定義，從前景和背景區域向內行進，並利用附近計算的F，B和α值（除了來自“已知”區域的這些值）構造定向高斯分佈，如圖d所示。此外，我們的方法制定了在明確定義的貝葉斯框架中計算融合引數的問題，並使用最大後驗（MAP）技術來解決它。在本節中，我們將詳細描述貝葉斯框架。

In MAP estimation, we try to find the most likely estimates for F, B, and α, given the observation C. We can express this as a maximization over a probability distribution P and then use Bayes’s rule to express the result as the maximization over a sum of log likelihoods:

在MAP估計中，我們試圖在給定觀察C的情況下找到最可能的F，B和α估計。我們可以將其表達為概率分佈P的最大化，然後使用貝葉斯規則將結果表示為最大化對數似然總和：

where L(·) is the log likelihood L(·) = logP(·), and we drop the P(C) term because it is a constant with respect to the optimization parameters. (Figure 1(h) illustrates the distributions over which we solve for the optimal F, B, and α parameters.)

其中L（·）是對數似然L（·）= logP（·），我們刪除P（C）項，因為它是關於優化引數的常數。（圖h說明了我們求解最優F，B和α引數的分佈。）

The problem is now reduced to defining the log likelihoods L(C | F, B, α), L(F), L(B), and L(α).

We can model the first term by measuring the difference between the observed color and the color that would be predicted by the estimated F, B, and α:

現在將問題簡化為定義對數似然L（C | F，B，α），L（F），L（B）和L（α）。

我們可以通過測量觀察到的顏色與估計的F，B和α預測的顏色之間的差異來建模第一項：

This log-likelihood models error in the measurement ofC and corresponds to a Gaussian probability distribution centered at C = αF + (1 − α)B with standard deviation σC.

該對數似然模型在C的測量中模型誤差並且對應於以C =αF+（1-α）B為中心的高斯概率分佈，具有標準偏差σC。

 We use the spatial coherence of the image to estimate the foreground term L(F). That is, we build the color probability distribution using the known and previously estimated foreground colors within each pixel’s neighborhood N. To more robustly model the foreground color distribution, we weight the contribution of each nearby pixel i in N according to two separate factors. First, we weight the pixel’s contribution by $a_{i}^{2}$ which gives colors of more opaque pixels higher confidence. Second, we use a spatial Gaussian fall off $g_{i}$ with σ = 8 to stress the contribution of nearby pixels over those that are further away. The combined weight is then $ω_{i}$ = $a_{i}^{2}$*$g_{i}$

我們使用影象的空間相干性來估計前景項L(F)。也就是說，我們使用每個畫素的鄰域N內的已知和先前估計的前景顏色來建立顏色概率分佈。為了更加魯棒地模擬前景顏色分佈，我們根據兩個單獨的因子來加權每個鄰近畫素i在N中的貢獻。首先，我們將畫素的貢獻加權$a_{i}^{2}$，這給了更多的不透明畫素更高的可信度顏色。其次，我們使用σ= 8的空間高斯衰減$g_{i}$來強調附近畫素對遠離那些畫素的貢獻。然後，合併的權重為$ω_{i}$ = $a_{i}^{2}$*$g_{i}$

Given a set of foreground colors and their corresponding weights, we first partition colors into several clusters using the method of Orchard and Bouman [7]. For each cluster, we calculate the weighted mean color F and the weighted covariance matrix ΣF:

給定一組前景色及其相應的權重，我們首先使用Orchard和Bouman [7]的方法將顏色分成幾個簇。對於每個聚類，我們計算加權平均顏色F和加權協方差矩陣ΣF：

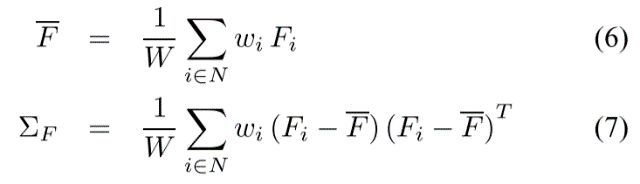
W=$\sum_{i\epsilon N}^{}$$\omega _{i}$ The log likelihoods for the foreground L(F) can then be modeled as being derived from an oriented elliptical Gaussian distribution, using the weighted covariance matrix as follows: 

然後可以使用加權協方差矩陣W=$\sum_{i\epsilon N}^{}$$\omega _{i}$ 將前景L（F）的對數似然建模為從定向橢圓高斯分佈匯出，如下：

The definition of the log likelihood for the background L(B) depends on which matting problem we are solving. For natural image matting, we use an analogous term to that of the foreground, setting  $\omega _{i}$ to $ (1-a_{i})^{2}g_{i}$ and substituting B in place of F in every term of equations (6), (7), and (8). For constant-color matting, we calculate the mean and covariance for the set of all pixels that are labelled as background. For difference matting, we have the background color at each pixel; we therefore use the known background color as the mean and a user-defined variance to model the noise of the background.

背景L（B）的對數似然的定義取決於我們正在解決的問題。對於自然影象消光，我們使用類似於前景的術語，將 $\omega _{i}$設定為$ (1-a_{i})^{2}g_{i}$ 

並且在等式（6），（7）的每個項中用B代替F，並且（8）對於恆定顏色消光，我們計算標記為背景的所有畫素集的均值和協方差。對於差異消光，我們在每個畫素處都有背景顏色; 因此，我們使用已知的背景顏色作為均值和使用者定義的方差來模擬背景噪聲。

In this work, we assume that the log likelihood for the opacity L(α) is constant (and thus omitted from the maximization in equation (4)). A better definition of L(α) derived from statistics of real alpha mattes is left as future work.

Because of the multiplications ofα with F and B in the log likelihood L(C | F, B, α), the function we are maximizing in (4) is not a quadratic equation in its unknowns. To solve the equation efficiently, we break the problem into two quadratic sub-problems. In the first sub-problem, we assume that α is a constant. Under this assumption, taking the partial derivatives of (4) with respect to F and B and setting them equal to 0 gives:

在這項工作中，我們假設不透明度L（α）的對數似然是常數（因此從等式（4）的最大化中省略）。從真實alpha融合的統計得出的更好的L(α)定義留作未來的工作。

由於在對數似然L（C | F，B，α）中α與F和B的乘積，我們在（4）中最大化的函式不是其未知數中的二次方程。為了有效地求解方程，我們將問題分解為兩個二次子問題。在第一個子問題中，我們假設α是常數。在這個假設下，對於F和B取（4）的偏導數並將它們設定為等於0給出：

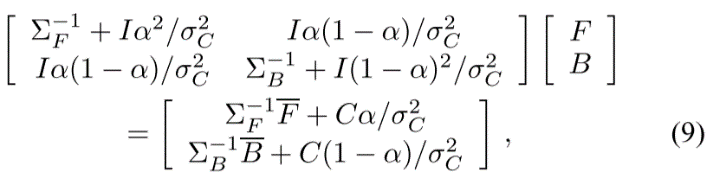
where I is a 3×3 identity matrix. Therefore, for a constant α, we can find the best parameters F and B by solving the 6×6 linear equation (9).

In the second sub-problem, we assume that F and B are constant, yielding a quadratic equation in α. We arrive at the solution to this equation by projecting the observed color C onto the line segment F B in color space:

其中I是3×3單位矩陣。因此，對於常數α，我們可以通過求解6×6線性方程（9）找到最佳引數F和B.

 在第二個子問題中，我們假設F和B是常數，在α中產生二次方程。我們通過將觀察到的顏色C投影到顏色空間中的線段F B上來得到該等式的解：

where the numerator contains a dot product between two color difference vectors. To optimize the overall equation (4) we alternate between assuming that α is fixed to solve for F and B using (9), and assuming that F and B are fixed to solve for α using (10). To start the optimization, we initialize α with the mean α over the neighborhood of nearby pixels and then solve the constant-α equation (9).

其中分子包含兩個色差向量之間的點積。為了優化整個等式（4），我們在假設α被固定以使用（9）求解F和B並假設F和B被固定以使用（10）求解α之間交替。為了開始優化，我們用附近畫素附近的平均α初始化α，然後求解常數α方程（9）。

When there is more than one foreground or background cluster, we perform the above optimization procedure for each pair of foreground and background clusters and choose the pair with the maximum likelihood. Note that this model, in contrast to a mixture of Gaussians model, assumes that the observed color corresponds to exactly one pair of foreground and background distributions. In some cases, this model is likely to be the correct model, but we can certainly conceive of cases where mixtures of Gaussians would be desirable, say, when two foreground clusters can be near one another spatially and thus can mix in color space. Ideally, we would like to support a true Bayesian mixture model. In practice, even with our simple exclusive decision model, we have obtained better results than the existing approaches.

當存在多個前景或背景聚類時，我們對每對前景和背景聚類執行上述優化過程，並選擇具有最大似然的對。注意，與高斯模型的混合相比，該模型假設觀察到的顏色恰好對應於一對前景和背景分佈。在某些情況下，這個模型可能是正確的模型，但我們當然可以設想需要高斯混合的情況，例如，當兩個前景聚類在空間上彼此靠近並因此可以在顏色空間中混合時。理想情況下，我們希望支援真正的貝葉斯混合模型。在實踐中，即使使用我們簡單的獨家決策模型，我們也獲得了比現有方法更好的結果。

4、Result and comparisons

We tried out our Bayesian approach on a variety of different input images, both for blue-screen and for natural image matting. Figure 2 shows four such examples. In the rest of this section, we discuss each of these examples and provide comparisons between the results of our algorithm and those of previous approaches. For more results and color images, please visit the URL listed under the title.

我們在各種不同的輸入影象上嘗試了貝葉斯方法，包括藍屏和自然影象消光。圖2顯示了四個這樣的例子。在本節的其餘部分，我們將討論這些示例中的每一個，並提供我們的演算法結果與以前方法的結果之間的比較。有關更多結果和彩色影象，請訪問標題下列出的URL。

Figure 2 Summary of input images and results. Input images (top row): a blue-screen matting example of a toy lion, a synthetic “natural image” of the same lion (for which the exact solution is known), and two real natural images, (a lighthouse and a woman). Input segmentation (middle row): conservative foreground (white), conservative background (black), and “unknown” (grey). The leftmost segmentation was computed automatically (see text), while the rightmost three were specified by hand. Compositing results (bottom row): the results of compositing the foreground images and mattes extracted through our Bayesian matting algorithm over new background scenes.

圖2輸入影象和結果摘要。輸入影象（頂行）：玩具獅子的藍屏消光示例，同一獅子的合成“自然影象”（已知確切解決方案），以及兩個真實的自然影象（燈塔和女人））。輸入分割（中間行）：保守前景（白色），保守背景（黑色）和“未知”（灰色）。最左邊的分割是自動計算的（見文字），而最右邊的三個是手動指定的。合成結果（底行）：合成前景影象和通過貝葉斯消光演算法在新背景場景中提取的融合的結果。

4.1 Blue screen Matting

We filmed our target object, a stuffed lion, in front of a computer monitor displaying a constant blue field. In order to obtain a ground-truth solution, we also took radiance-corrected, high dynamic range [3] pictures of the object in front of five additional constant-color backgrounds. The ground-truth solution was derived from these latter five pictures by solving the overdetermined linear system of compositing equations (1) using singular value decomposition.

我們在顯示恆定藍色區域的計算機顯示器前拍攝了我們的目標物體，一隻毛絨獅子。為了獲得地面實況解決方案，我們還在五個額外的恆定顏色背景前面拍攝了物體的輻射校正，高動態範圍[3]圖片。通過使用奇異值分解求解合成方程（1）的超定線性系統，從後五個圖中得出了真實性解。

Both Mishima’s algorithm and our Bayesian approach require an estimate of the background color distribution as input. For blue-screen matting, a preliminary segmentation can be performed more-or-less automatically using the Vlahos equation (2) from Section 2. Setting a1 to be a large number generally gives regions of pure background (where α ≤ 0), while setting a1 to a small number gives regions of pure foreground (where α ≥ 1). The leftmost image in the middle row of Figure 2 shows the preliminary segmentation produced in this way, which was used as input for both Mishima’s algorithm and our Bayesian approach.

Mishima’s演算法和貝葉斯方法都需要估計背景顏色分佈作為輸入。對於藍屏消光，可以使用第2節中的Vlahos方程（2）自動執行初步分割。將a1設定為大數通常給出純背景區域（其中α≤0），而將a1設定為較小的數字會給出純前景區域（其中α≥1）。圖2中間行的最左邊的影象顯示了以這種方式產生的初步分割，它被用作Mishima演算法和貝葉斯方法的輸入。

In Figure 3, we compare our results with Mishima’s algorithm and with the ground-truth solution. Mishima’s algorithm exhibits obvious “blue spill” artifacts around the boundary, whereas our Bayesian approach gives results that appear to be much closer to the ground truth.

在圖3中，我們將我們的結果與Mishima的演算法和地面實況解決方案進行了比較。Mishima的演算法在邊界周圍顯示出明顯的“藍色溢位”偽影，而我們的貝葉斯方法給出了出現的結果

更接近實際情況。

Figure 3 Blue-screen matting of lion (taken from leftmost column of Figure 2). Mishima’s results in the top row suffer from “blue spill.” The middle and bottom rows show the Bayesian result and ground truth, respectively.

4.2 Natural image Matting

Figure 4 provides an artificial example of “natural image matting,” one for which we have a ground-truth solution. The input image was produced by taking the ground-truth solution for the previous blue-screen matting example, compositing it over a (known) checkerboard background, displaying the resulting image on a monitor, and then re-photographing the scene. We then attempted to use four different approaches for re-pulling the matte: a simple difference matting approach (which takes the difference of the image from the known background, thresholds it, and then blurs the result to soften it); Knockout; the Ruzon and Tomasi algorithm, and our Bayesian approach. The ground-truth result is repeated here for easier visual comparison. Note the checkerboard artifacts that are visible in Knockout’s solution. The Bayesian approach gives mattes that are somewhat softer, and closer to the ground truth, than those of Ruzon and Tomasi.

圖4提供了一個“自然影象消光”的人工例子，我們有一個真實的解決方案。輸入影象是通過採用前一個藍屏消光示例的地面實況解決方案，在（已知的）棋盤背景上合成，在監視器上顯示結果影象，然後重新拍攝場景而產生的。 然後我們嘗試使用四種不同的方法來重新拉動融合：一種簡單的差異融合方法（它從已知背景中獲取影象的差異，對其進行閾值處理，然後模糊結果以使其柔化）;Knockout,Ruzon和Tomasi演算法，以及我們的貝葉斯方法。這裡復現了真實的地面場景，以便於進行視覺比較。請注意Knockout解決方案中可見的棋盤工件。 與Ruzon和Tomasi相比，貝葉斯方法給出了更柔和，更接近ground truth的融合。

Figure 4 “Synthetic” natural image matting. The top row shows the results of difference image matting and blurring on the synthetic composite image of the lion against a checkerboard (column second from left in Figure 2). Clearly, difference matting does not cope well with fine strands. The second row shows the result of applying Knockout; in this case, the interpolation algorithm poorly estimates background colors that should be drawn from a bimodal distribution. The Ruzon-Tomasi result in the next row is clearly better, but exhibits a significant graininess not present in the Bayesian matting result on the next row or the ground-truth result on the bottom row.

圖4“合成”自然影象消光。頂行顯示了獅子與棋盤的合成影象上的差異影象消光和模糊的結果（圖2中左起第二列）。顯然，差異消光不能很好地應對細線。第二行顯示應用Knockout的結果; 在這種情況下，插值演算法很難估計應該從雙峰分佈中提取的背景顏色。下一行的Ruzon-Tomasi結果顯然更好，但在下一行的貝葉斯消光結果或底行的真實結果中表現出明顯的顆粒度。

Figure 5 repeats this comparison for two (real) natural images (for which no difference matting or ground-truth solution is possible). Note the missing strands of hair in the close-up for Knockout’s results. The Ruzon and Tomasi result has a discontinuous hair strand on the left side ofthe image, as well as a color discontinuity near the center of the inset. In the lighthouse example, both Knockout and Ruzon-Tomasi suffer from background spill. For example, Ruzon-Tomasi allows the background to blend through the roof at the top center of the composite inset, while Knockout loses the railing around the lighthouse almost completely. The Bayesian results exhibit none of these artifacts.

圖5重複了兩個（真實的）自然影象的比較（對此沒有差異消光或地面真實解決方案）。注意Knockout結果中特寫的頭髮缺失。Ruzon和Tomasi結果在影象的左側具有不連續的髮束，以及在插圖的中心附近的顏色不連續性。在燈塔示例中，Knockout和Ruzon-Tomasi都遭遇背景洩漏。例如，Ruzon-Tomasi允許背景通過複合材料插入物頂部中心的屋頂混合，而Knockout幾乎完全失去燈塔周圍的欄杆。貝葉斯結果沒有表現出這些偽影。

Figure 5 Natural image matting. These two sets of photographs correspond to the rightmost two columns of Figure 2, and the insets show both a close-up of the alpha matte and the composite image. For the woman’s hair, Knockout loses strands in the inset, whereas Ruzon-Tomasi exhibits broken strands on the left and a diagonal color discontinuity on the right, which is enlarged in the inset. Both Knockout and Ruzon-Tomasi suffer from background spill as seen in the lighthouse inset, with Knockout practically losing the railing.

圖5自然影象消光。這兩組照片對應於圖2中最右邊的兩列，並且插圖顯示了alpha融合和合成影象的特寫。對於女人的頭髮，Knockout在插圖中丟失了股線，而Ruzon-Tomasi在左邊展示了斷裂的股線，在右邊展示了對角線顏色不連續，在插圖中放大了。Knockout和Ruzon-Tomasi都遭遇了背景溢位，如燈塔插圖所示，Knockout幾乎失去了欄杆。

5、Conclusions

In this paper, we have developed a Bayesian approach to solving several image matting problems: constant-color matting, difference matting, and natural image matting. Though sharing a similar probabilistic view with Ruzon and Tomasi’s algorithm, our approach differs from theirs in a number of key aspects; namely, it uses (1) MAP estimation in a Bayesian framework to optimize α, F and B simultaneously, (2) oriented Gaussian covariances to better model the color distributions, (3) a sliding window to construct neighborhood color distributions that include previously computed values, and (4) a scanning order that marches inward from the known foreground and background regions. To sum up, our approach has an intuitive probabilistic motivation, is relatively easy to implement, and compares favorably with the state of the art in matte extraction.

在本文中，我們開發了一種貝葉斯方法來解決幾個影象消光問題：恆色消光，差異消光和自然影象消光。 雖然與Ruzon和Tomasi的演算法共享類似的概率檢視，但我們的方法在許多關鍵方面與他們的方法不同; 即，它使用（1）貝葉斯框架中的MAP估計同時優化α，F和B，（2）定向高斯協方差以更好地模擬顏色分佈，（3）構建鄰域顏色分佈的滑動視窗，包括先前計算的 值，以及（4）從已知前景和背景區域向內行進的掃描順序。總之，我們的方法具有直觀的概率動機，相對容易實現，並且與現有的消光提取技術相比是有利的。

In the future, we hope to explore a number of research directions. So far, we have omitted using priors on alpha. We hope to build these priors by studying the statistics of ground truth alpha mattes, possibly extending this analysis to evaluate spatial dependencies that might drive an MRF approach to image matting. Next, we hope to extend our framework to support mixtures of Gaussians in a principled way, rather than arbitrarily choosing among paired Gaussians as we do currently. Finally, we plan to extend our work to video matting with soft boundaries.

在未來，我們希望探索一些研究方向。到目前為止，我們已經省略了在alpha上使用priors。 我們希望通過研究地面實況alpha融合的統計資料來構建這些先驗，可能會擴充套件此分析以評估可能驅動MRF方法進行影象融合的空間依賴性。接下來，我們希望擴充套件我們的框架，以原則的方式支援高斯混合，而不是像我們目前那樣隨意選擇配對的高斯。最後，我們計劃將我們的工作擴充套件到具有軟邊界的視訊融合。