蒙特卡洛演算法——投點求圓周率Pi
蒙特卡洛演算法:蒙特卡洛是美國摩納哥的一個城市,以賭博聞名於世。蒙特卡洛演算法借用這一城市的名稱是為了象徵性的表明該方法的概率統計特點。蒙特卡洛演算法作為一種計算方法,是由S.M.烏拉姆和J.馮諾依曼在20世紀40年代中葉為研製核武器的需要而提出的。
蒙特卡洛方法的基本思想雖然早已被人提出,例如在古典概率中的著名法國數學家布豐利用投針求圓周率Pi值,卻很少被使用。直到電子計算機出現後,使得人們可以通過電子計算機來模擬巨大數目的隨機試驗過程,使得蒙特卡洛方法得到廣泛地應用。
用蒙特卡洛投點法計算Pi的值;
在一個邊長為a的正方形內一均勻概率隨機投點,該點落在此正方形的內切圓中的概率即為內切圓與正方形的面積比值,即:Pi * (a / 2)^2 : a^2 = Pi / 4。
%總的實驗次數
n = input('請輸入n:');
%落在圓中點的次數
m = 0;
%使用的圓的半徑
a = 2;
%迴圈實驗
for i = 1:n
x = rand * a / 2;
y = rand * a / 2;
if (x^2 + y^2 <= (a/2)^2)
m = m + 1;
end
end
%顯示結果
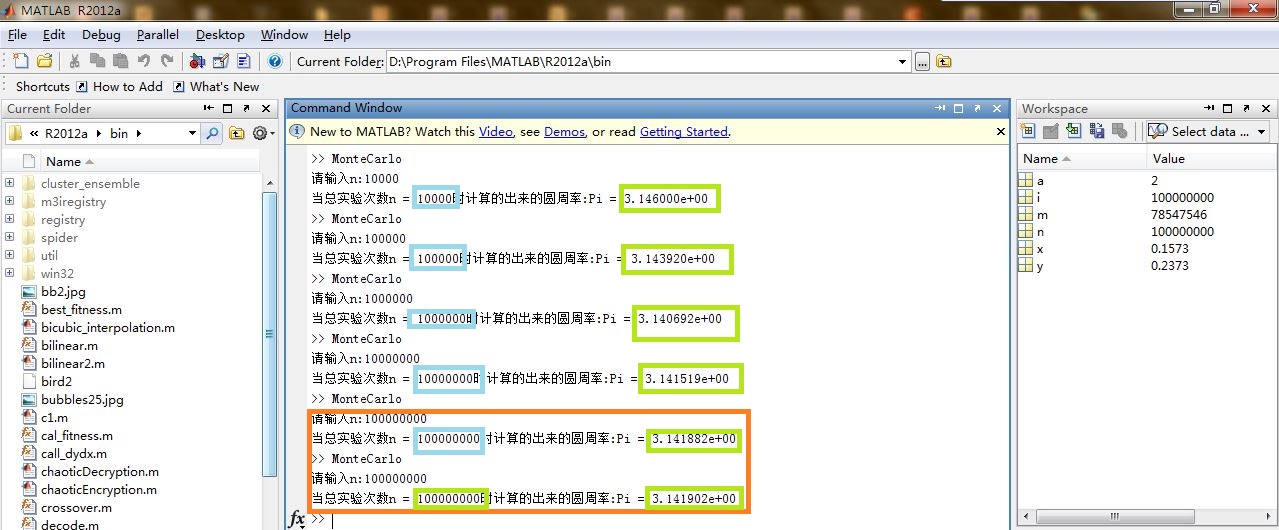
fprintf('當總實驗次數n = %d時計算出來的圓周率:Pi = %d\n',n, 4 * m / n);從實驗結果可以分析得出:
1.隨著投點的次數增加,圓周率Pi計算的準確率在增加;
2.但當次數達到一定規模時,準確率精度增加在減緩,其原因是生成的隨機數是偽隨機的,這也是蒙特卡洛演算法達不到祖沖之求圓周率精度的內在原因;
3.同時在進行兩次的1億次投點中也可以發現,對於相同的投點數由於實驗本身的隨機性每次的實驗結果是不同的。
相關推薦
蒙特卡洛演算法——投點求圓周率Pi
蒙特卡洛演算法是以概率和統計的理論、方法為基礎的一種計算方法,將所求解的問題同一定的概率模型相聯絡;用電子計算機實現統計模擬和抽樣,以獲得問題的近似解,故又稱統計模擬法或統計實驗法。 蒙特卡洛演算法:蒙特卡洛是美國摩納哥的一個城市,以賭博聞名於世。蒙特卡洛演算法借用這一城市
蒙特卡洛投點求近似PI
PI =3.141592653589793238462643383279502..... 怎麼做的呢 是在單位圓裡面操作的 S=2PI r^2 然後r=1 面積就是PI 外接正方形面積為4 那麼很多點 掉在圓裡面的概率就是PI/4 這個概率P就相當於你在正方形範圍內投很多點 在圓裡
1067 例題5-7 求圓周率pi的近似值
用如下公式求圓周率PI的近似值,直到發現某一項的絕對值小於10-6為止(該項不累加)。要求輸出的結果總寬度佔10位,其中小數部分為8位。程式中使用浮點型資料時,請定義為雙精度double型別。如果需要計算絕對值,可以使用C語言數學庫提供的函式fabs,如求x的絕對值,則為fabs(x).
初學C語言:求圓周率pi的近似值(pi/4=1-1/3+1/5-1/7...)
#include<stdio.h> #include<math.h> int main() { double pi1,pi2,j=0,i=0,u=0,v=0;
蒙特卡洛演算法求PI
利用蒙特卡洛法隨機生成任意點,求出PI 原始碼: import java.awt.*;import java.util.LinkedList;import javax.swing.*;public class AlgoFrame extends JFrame{ priv
java蒙特卡洛演算法求PI值(視覺化)及三門問題
蒙特卡洛演算法求PI值 工具類 package com.egeo.jframetext; import java.awt.BasicStroke; import java.awt.Color; import java.awt.FontMetrics
各種求圓周率π的演算法(蒙特卡洛法的Java實現)
什麼是演算法?簡單地說,演算法就是有窮規則構成的用於解決某一類問題的運算序列或執行步驟。在《演算法之美:隱匿在資料結構背後的原理》第1章中我們講到要解決一個問題可能會有不同的方法,當時所舉的例子就是求圓周率π的近似值。對於這個問題你能想到多少種演算法呢? 探祕演算
tornadofx使用circle、AnimationTimer、timeline動畫演示蒙特卡洛演算法求PI值
演示地址:https://www.bilibili.com/video/av59421525 import javafx.a
蒙特卡洛法求圓周率100億資料
程式碼 import time import random hits=0 pi=0 DARTS=100000*100000 start=time.perf_counter() for i in range(DARTS): x,y=random.random(),random.
程式基本演算法習題解析 求pi的近似值
思路: pi/4 = 1 - 1/3 +1/5 -1/7 + ... 附上程式碼: // Chapter5_3.cpp : Defines the entry point for the application. // 求pi的近似值 #include "stdafx.h"
蒙特卡洛法求圓周率
程式碼 import time import random hits=0 pi=0 DARTS=100000*100000 start=time.perf_counter() for i in rang
超詳細Tarjan演算法總結,求強連通分量,割點,割邊,有重邊的割邊
Tarjan是一個人,他一身中發明了很多演算法,就這幾個演算法最為出名。 1、求有向圖的強連通分量,那麼什麼是強連通分量呢,就是一個頂點集合,任意兩個頂點間都可以互相到達。一個頂點也是強聯通分量如果圖中任意兩點可以互相到達,則此圖強連通。下圖中頂點{1,0,2}屬於一個強聯
一個例子讓你明白一個演算法-Dijkstra(求源點到各頂點最短路徑)
演算法思想 1.在一個圖中,把所有頂點分為兩個集合P,Q(P為最短路徑集合,Q為待選集合),用dis陣列儲存源點到各個頂點的最短路徑(到自身為0)。 2.初始化P集合,就是加入源點到該集合,並在ma
@演算法 - [email protected] 多項式的多點求值與快速插值
目錄 @0 - 參考資料@ @1 - 多點求值@ @理論推導@ @參考程式碼@ @例題與應用@ @2 - 快速插值@ @理論推導@ @(不建議參考的)程式碼@ @例題與應用@(暫無) @0 - 參考資料@ Cy
hdu 4587 TWO NODES(tarjan演算法 刪兩個點求最多剩餘聯通分量)
TWO NODES Time Limit: 24000/12000 MS (Java/Others) Memory Limit: 65535/32768 K (Java/Others) Total Submission(s): 3091 &
Dijkstra [迪傑斯特拉]演算法思路(求單點到其他每個點的各個最短路徑)Floyd演算法:任意兩點間最短距離
先給出一個無向圖 用Dijkstra演算法(迪傑斯特拉演算法)找出以A為起點的單源最短路徑步驟如下 應用Dijkstra演算法計算從源頂點1到其它頂點間最短路徑的過程列在下表中。 Dijkstra演算法的迭代過程: Floyd演算法思想: 1、從任意一條單邊路徑開
HDU - 3584 Cube (三維樹狀數組 + 區間改動 + 單點求值)
btn either -o mem 求值 popu -s onos column HDU - 3584 Cube Time Limit: 1000MS Memory Limit: 65536KB 64bit IO
hdu4612 無向圖中隨意加入一條邊後使橋的數量最少 / 無向圖縮點+求樹的直徑
child iostream tracking amp min esp _id 矛盾 cstring 題意如上,含有重邊(重邊的話,倆個點就能夠構成了邊雙連通)。 先縮點成樹,在求數的直徑,最遠的連起來,剩下邊(橋)的自然最少。這裏學習了樹的直徑求法:第一次選隨意
poj1966枚舉源匯點求點連通度
+= sets sent line ise order less several dir Cable TV Network Time Limit: 1000MS Memory Limit: 30000K Total Submissions: 4851 A
hdu 1556 Color the ball(線段樹區間維護+單點求值)
code AR else map 區間維護 strong ssi 求值 blank 傳送門:Color the ball Color the ball Time Limit: 9000/3000 MS (Java/Others) Memory Limit: 32768