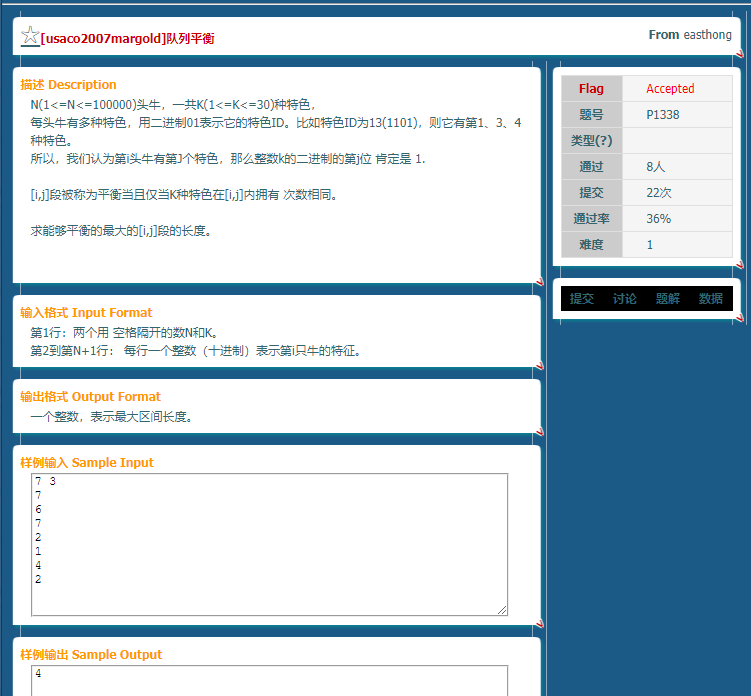
這題其實不難啊,為啥沒人寫.

　　理解完題意,首先預處理應該都會.然後考慮如何統計答案.直接想到一個暴力的方法:O(n^2)列舉左右端點,O(k)判斷是否各個位置上的數都相同.

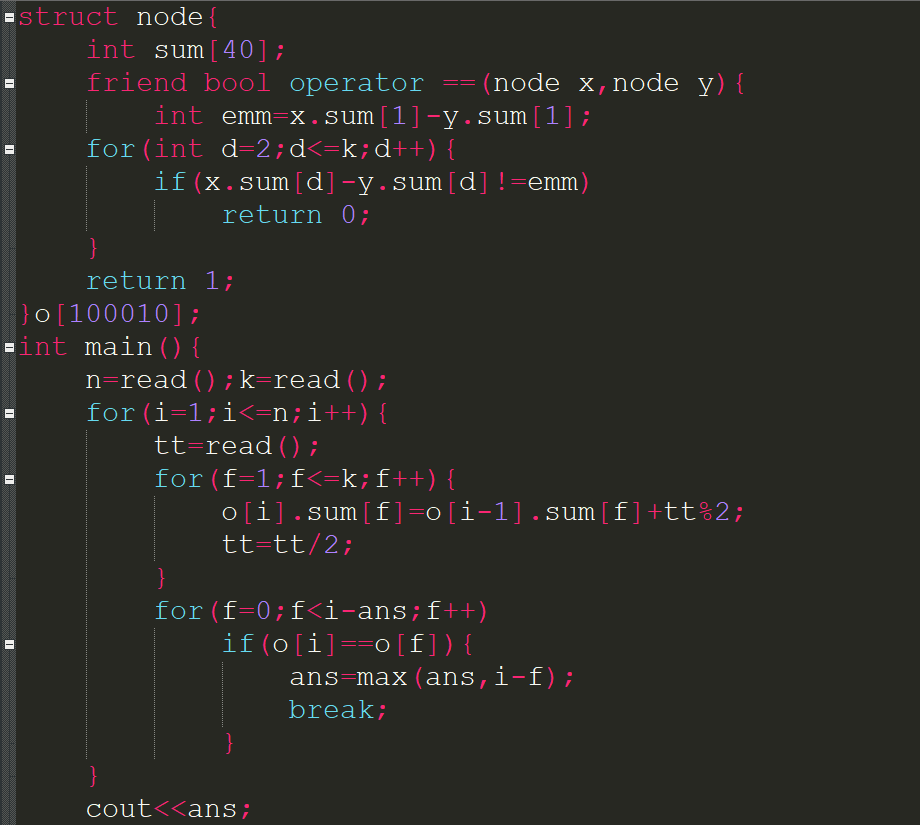
　　然後考慮如何把一個n改成一個log(n)?k比較小,可以往這邊考慮

　　先考慮下面兩個例子.這裡每一位表示1,i時出現1的總數.

o[i].a[j]2 3 5  1
o[f].a[j]7 8 10 6

　　這兩個端點顯然合法.如何描述這種"相同性"呢?我有兩種方法.一種是都減去minn(a[j]),得到這樣的結果.

都減1 1 2 4 0
都減6 1 2 4 0
 

　　或者弄一個差分陣列.原來是j∈[1,k],差分陣列顯然只需要[2,k]相同即可.

差分
? 1 2 -4

　　然後如何更新答案呢?我想到了三行離散化.但是應該還有一種更好的方法:map.直接用結構體做下標還不是美滋滋?

using namespace std;
int i,f,tt;
int n,k,ans;
struct node{
    int a[40],sum[40];
    friend bool operator <(node x,node y){
    for(int d=2;d<=k;d++){
        if
 
(x.a[d]!=y.a[d])
            return x.a[d]<y.a[d];
    }
    return 0;
}o[100000];
map<node,int>mm;
int main()
{
    n=read();k=read();
    if(k==1){cout<<n;return 0;}
    mm[o[0]]=1;//記錄全0的時候的下標為1
    for(i=1;i<=n;i++){
        tt=read();
        for(f=1;f<=k;f++){
            o[i].sum[f]
 
=o[i-1].sum[f]+tt%2;
            tt=tt/2;
        }
        for(f=2;f<=k;f++)
            o[i].a[f]=o[i].sum[f]-o[i].sum[f-1];//差分陣列
        tt=mm[o[i]];
        if(tt!=0) ans=max(ans,i-tt+1);//更新答案
        else      mm[o[i]]=i+1;//記錄最先出現的下標.為了照顧o[0]只好賦為下標+1
    }
    cout<<ans;
    return 0;
}