PRML(一)如何根據貝葉斯理論推導多項式曲線擬合問題的cost function
馬上要成為一個ML/DL方向的工程師,PRML作為經典教材,對於理解一些常用演算法的intuition和motivation是非常有益的。雖然是2006年出版的一本書,但是有很多內容仍然值得學習和反思。加之本書有一些習題可以鞏固思考,今天開始踏入PRML的學習。
① 理論基礎
如何根據貝葉斯理論推導多項式曲線擬合問題的損失函式,這個需要的基本概率論基礎如下
加法公式
乘法公式
貝葉斯公式
其中,,
還有值得注意的是,在貝葉斯公式中,分母被視為讓條件概率之和為1(所有yi情況)的normalization constant——正則因子。
在後面敘述利用引數來作多項式擬合曲線中,我們假設先捕捉到關於的概率,用先驗概率表示。觀測資料為,用條件概率表示。可以視為引數向量的函式,稱為似然函式。因此,可以採用貝葉斯定理,形式如下:
PRML的作者Bishop不止一次強調:在貝葉斯公式中的作用就是讓左邊的關於的積分為1,限制其規模,算是一個正則常數(normalization constatnt),即
在貝葉斯理論中,我們認為是不確定的,而是已知的——通過觀測得到的唯一一組資料。貝葉斯理論的優點在於:先驗知識的產生是自然的。比如對55開的投硬幣問題,如果連續投3次,每次都是正面朝上,那麼傳統的最大似然估計估計就會錯誤的認為正面朝上的概率為1。而貝葉斯方法則會給出一個不會出現這種極端情況的先驗概率。
當然,貝葉斯方法也有缺點,它的典型缺點是:先驗分佈是不提供資訊的。 貝葉斯方法的先驗概率選擇是基於數學上的方便而非其它先驗資訊的反映,所以,如果使用的貝葉斯方法先前的選擇糟糕,那麼會給糟糕的結果很高的置信度。
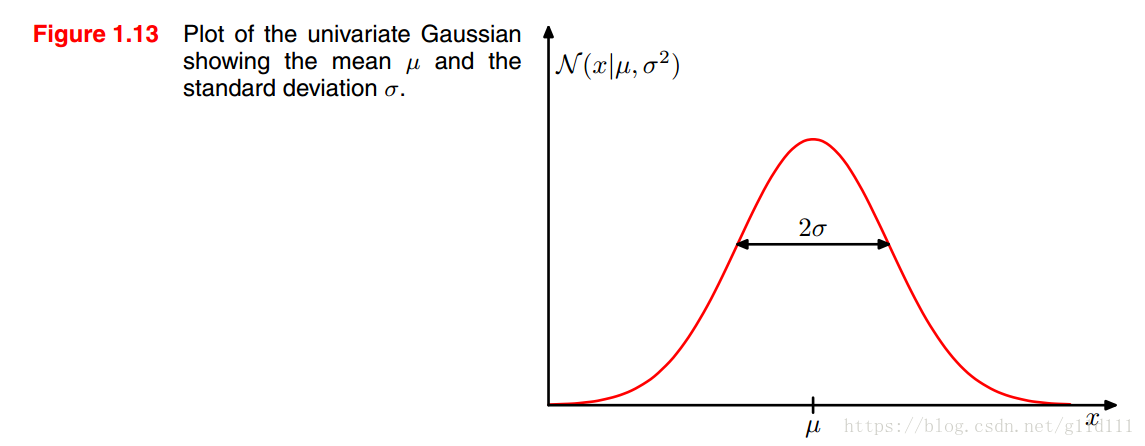
下面介紹一下高斯分佈/正態分佈,它是最為重要的一種分佈,對於單個實值變數,其高斯分佈為:
其中,為均值,為方差,為標準差。這裡還定義了一個,稱為精度。
當為維向量組成的連續型變數時,其高斯分佈的新形式為:
馬上要成為一個ML/DL方向的工程師,PRML作為經典教材,對於理解一些常用演算法的intuition和motivation是非常有益的。雖然是2006年出版的一本書,但是有很多內容仍然值得學習和反思。加之本書有一些習題可以鞏固思考,今天開始踏入PRML的
上研究生的時候,一心想讀生物資訊學的方向,由此也選修了生物數學,計算生物學等相關課程。給我印象最深的是給我們計算生物學的主講老師,他北大數學系畢業,後來做起了生物和數學的交叉學科研究。課上講的一些演算法比如貝葉斯,馬爾科夫,EM等把我給深深折磨了一遍。由於那時候 pan 技巧 nbsp 增強 就是 使用 分類問題 預測 結果 一、條件概率
在學習計算p1和p2概率之前,我們需要了解什麽是條件概率,就是指在事件B發生的情況下,事件A發生的概率,用P(A|B)來表示。
根據文氏圖,可以很清楚地看到在事件B發生的情況下,事件A發
目錄
0. 前言
1. 條件概率
2. 樸素貝葉斯(Naive Bayes)
3. 樸素貝葉斯應用於文字分類
4. 實戰案例
4.1. 垃圾郵件分類案例
學習完機器學習實戰的樸素貝葉斯,簡單的做個筆記。文中
大資料、人工智慧、海難搜救、生物醫學、郵件過濾,這些看起來彼此不相關的領域之間有什麼聯絡?答案是,它們都會用到同一個數學公式——貝葉斯公式。它雖然看起來很簡單、很不起眼,但卻有著深刻的內涵。那麼貝葉斯公式是如何從默默無聞到現在廣泛應用、無所不能的呢?
◆ ◆ ◆
什麼是貝
注意:貝葉斯是一個偉大的發明,給人工智慧以及社會發展帶來了巨大貢獻**。
引言
隨著對貝葉斯的不斷應用,對貝葉斯有了從新的認識,以前認為貝葉斯知識用來解決二分類問題,是大錯特錯發現貝葉斯是一種
前言
frequentist statistics:模型引數是未知的定值,觀測是隨機變數;思想是觀測數量趨近於無窮大+真實分佈屬於模型族中->引數的點估計趨近真實值;代表是極大似然估計MLE;不依賴先驗。
Bayesian statistics:模型引數是隨機變數,
傳統演算法(五)
貝葉斯演算法
一、貝葉斯定理
簡介
貝葉斯定理是18世紀英國數學家托馬斯·貝葉斯(Thomas Bayes)提出得重要概率論理論;貝葉斯方法源於他生前為解決一個“逆概”問題寫的一篇文章
機器學習所研究的主要內容,是關於在計算機上從資料中產生“模型”的演算法,這個產生的模型大體上可以分為“判別式模型”和“生成式模型”兩大類。
其中判別式模型是給定x,通過直接對條件概率分佈P(y|x)進行建模來預測y。這種方法尋找不同類別的最優分類面,反映的是異類資料之間的差異。之前幾篇文章中介紹
機器學習 - 樸素貝葉斯(下)- 樸素貝葉斯分類器
樸素貝葉斯
重要假設
特徵型別
樸素貝葉斯分類模型
舉例
貝葉斯估計
模型特點
機器學習數學原理(4)——樸素貝葉斯模型
樸素貝葉斯模型(Naive Bayes Model),是一種基於貝葉斯定理與特徵條件獨立假設的分類方法,與決策樹模型(Decision Tree Model)同為目前使用最廣泛的分類模型之一,在各個領域都有廣泛的應用,例如我們經常會用到的垃圾 其中,P(C|x)表示觀測到資料x時事件C發生的條件概率,我們稱為後驗概率(posterior probability);P(C)=P(C=1)是事件C=1發生時的概率,稱為先驗概率(prior probabilty),因為這是在觀察到資料x之前就已經得到的關於C的知識;P(x|C)稱為類似然,與
OpenCV的機器學習類定義在ml.hpp檔案中,基礎類是CvStatModel,其他各種分類器從這裡繼承而來。
今天研究CvNormalBayesClassifier分類器。
1.類定義
在ml.hpp中有以下類定義:
class CV_EXPORTS_W CvNorm
樸素貝葉斯法
4.1 naive Bayes的學習與分類
4.1.1 基本方法
設輸入空間為n維向量的集合X⊆Rn,輸出空間為類標記的集合Y={c1,c2,...,cK}。輸入為特徵向量x∈X,輸出為類標記y∈Y。X是定義在輸入空間上的隨機變數,Y
演算法三:樸素貝葉斯演算法
在貝葉斯決策中,對於先驗概率p(y),分為已知和未知兩種情況。
1. p(y)已知,直接使用貝葉斯公式求後驗概率即可;
2. p(y)未知,可以使用聶曼-皮爾遜決策(N-P決策)來計算決策面。
而最大最小損失規則主要就是使用解決最小損失規則時先驗概率未知或難以計算的問題的
樸素貝葉斯法是基於貝葉斯定理與特徵條件獨立假設的分類方法。簡單來說,樸素貝葉斯分類器假設樣本每個特徵與其他特徵都不相關。舉個例子,如果一種水果具有紅,圓,直徑大概4英寸等特徵,該水果可以被判定為是蘋果。儘管這些特徵相互依賴或者有些特徵由其他特徵決定,然而樸素貝葉斯分類器認
第四章 基於概率論的分類方法:樸素貝葉斯
4-1 基於貝葉斯決策理論的分類方法
優點:在資料較小的情況下仍然有效,可以處理多類別問題
缺點:對於輸入資料的準備方式較為敏感。
適用資料型別:標稱型資料。
假設現在我們有一個數據集,它由兩類資
1.安裝中文分詞器
由於本文是對中文文字進行分類,故需要用到中文分詞器,而結巴分詞則是Python支援較好的一款分詞器。
使用命令安裝:
pip3 install jieba3k
或者下載結巴分詞檔案【下載】
結巴分詞測試:
結巴分詞支援三種分詞模式:
精確模式,也是結巴
一、極大似然估計
在上一筆記中,經過推導,得到了樸素貝葉斯分類器的表示形式:
y=argmaxckP(Y=ck)∏jP(X(j)=x(j)|Y=ck)(1)
也就是說,樸素貝葉斯方法的學習是對概率P(Y=ck)和P(X(j)=x(j)|Y=ck)的
樸素貝葉斯演算法也是一種常用的分類演算法,尤其在對文字文件分類的學習任務中,樸素貝葉斯分類是最有效的演算法之一。所謂的樸素,即假設在給定目標值時屬性值之間相互條件獨立,雖然這一假設看似不合理,但其最終的分類效果卻普遍較好。
一、概述
1、貝葉斯公式
2、最大後驗假設(MA
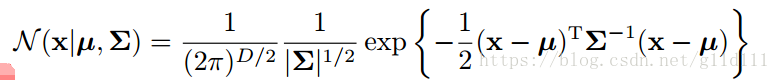
這裡,
相關推薦
PRML(一)如何根據貝葉斯理論推導多項式曲線擬合問題的cost function
機器學習筆記(一)樸素貝葉斯的Python程式碼實現
機器學習讀書筆記(四)樸素貝葉斯基礎篇之網站賬號分類
機器學習實戰(三)樸素貝葉斯NB(Naive Bayes)
大資料背後的神祕公式(上):貝葉斯公式
機器學習 (九) 深入淺出貝葉斯-Thomas Bayes
最大似然估計(MLE)、最大後驗概率估計(MAP)以及貝葉斯學派和頻率學派
[學習筆記]機器學習——演算法及模型(五):貝葉斯演算法
機器學習筆記(六):貝葉斯分類器
機器學習 - 樸素貝葉斯(下)- 樸素貝葉斯分類器
機器學習數學原理(4)——樸素貝葉斯演算法
【機器學習】(5):貝葉斯決策定理
OpenCV機器學習(1):貝葉斯分類器實現程式碼分析
統計學習筆記(四)樸素貝葉斯法
R語言與機器學習學習筆記(分類演算法)(3)樸素貝葉斯
統計學習筆記(4)——樸素貝葉斯法
Python《機器學習實戰》讀書筆記(四)——樸素貝葉斯
Python與機器學習(五)樸素貝葉斯分類
機器學習筆記(六)——樸素貝葉斯法的引數估計
機器學習演算法(三)——樸素貝葉斯演算法及R語言實現方法