一、對數

二、程式碼

 1 def binary_search(lists, item):
 2     # low和high用於跟蹤要在其中查詢的列表的部分
 3     low = 0
 4     high = len(lists)-1
 5 
 6     while low <= high:  # 只要範圍沒有縮小到只包含一個元素
 7         mid = (low + high)/2 #就檢查中間的元素
 8 
 9         guess = lists[mid]
10         if guess == item: #找到元素
11             return
 
 mid
12         if guess > item: # 猜的數字大了
13             high = mid-1
14         else:            # 差的數字小了
15             low = mid+1
16     #  沒有指定的元素
17     return None
18 
19 my_list = [1, 3, 5, 7, 9]
20 print(len(my_list))
21 print (binary_search(my_list, 3))
22 print (binary_search(my_list, -1))
 

三、執行時間

　　如果列表包含100個元素，最多要猜7次；

　　如果列表包含40億個數字，最多需猜32次。二分查詢的執行時間為對數時間（或log時間）

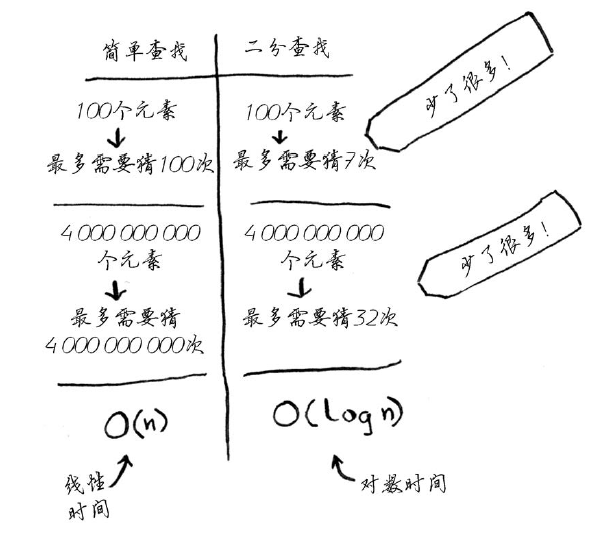
四、大O表示法

　　大O表示法是一種特殊的表示法，指出了演算法的速度有多快。

　　大O表示法指出了演算法有多快。例如，假設列表包含n個元素。簡單查詢需要檢查每個元素，因此需要執行n次操作。使用大O表示法，這個執行時間為O(n)。

　　單位秒呢？沒有——大O表示法指的並非以秒為單位的速度。

　　大O表示法讓你能夠比較運算元，它指出了演算法執行時間的增速。

　　下面按從快到慢的順序列出了你經常會遇到的5

　　1、O(log n)，也叫對數時間，這樣的演算法包括二分查詢。
　　2、O(n)，也叫線性時間，這樣的演算法包括簡單查詢。
　　3、O(n * log n)，這樣的演算法包括第4章將介紹的快速排序——一種速度較快的排序演算法。
　　4、O(n2)，這樣的演算法包括第2章將介紹的選擇排序——一種速度較慢的排序演算法。
　　5、O(n!)，這樣的演算法包括接下來將介紹的旅行商問題的解決方案——一種非常慢的演算法。

說明

　　1、僅當列表是有序的時候，二分查詢才管用。

　　2、談論演算法的速度時，我們說的是隨著輸入的增加，其執行時間將以什麼樣的速度增加。

　　3、演算法的執行時間用大O表示法表示。

　　4、O(log n)比O(n)快，當需要搜尋的元素越多時，前者比後者快得越多。

　　5、演算法執行時間並不以秒為單位。

　　參考書籍：演算法圖解