react-native-art畫二次貝塞爾曲線實現
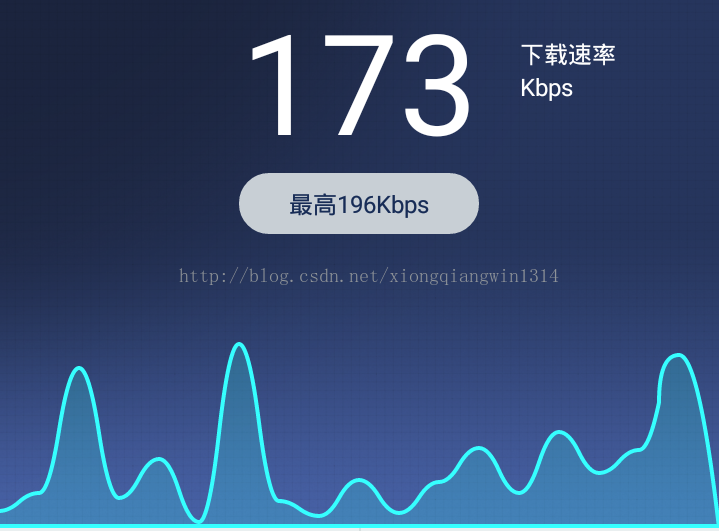
1、關於react-native ART庫的使用,目前網上能搜到的少之又少,簡書上的一篇react-native-art 繪圖入門,從基本上講解了一下react-native-art的使用方法,但是隻是簡單的橫豎曲線的繪製,但專案中有一個需求就是繪製網速的速率曲線,
(專案最終效果)
那麼如果按照react-native-art繪圖入門上給的寥寥幾個介面是不可能實現畫出一個平滑曲線的目的的,為此又參考了一篇在React Native中使用 ART,該篇中使用react-native-art-svg庫,其中第一個坑點就是,react-native-art-svg庫需要react-native的版本(具體版本忘記了,好象是2時代的版本0.28吧好像)低於目前專案中所用的版本(專案版本0.35),然後一陣搜尋之後發現,react-native-art-svg目前已經進化成為react-native-svg庫,但要求react-native版本>=0.38(好象是這個值,但反正大於0.35),因此在git上切換分支嘗試用react-native-svg時,發現出現了一些未知的問題,比如scrollView不能往下拖動了,並且暫時沒用精力去升降級RN版本,於是在嘗試了最新版本RN之後,選擇放棄react-native-svg庫。
2、但是如需要畫出上述曲線圖,SVG中的二次貝塞爾曲線是必不可少的,因此不死心,心想,既然ART,是一個在React中繪製向量圖形的JS類庫。這個類庫抽象了一系統的通用介面,統一了SVG,canvas,VML這類向量圖形在React中的書寫格式。那麼,ART庫肯定也是集成了SVG的path屬性,並且支援利用path畫二次貝塞爾曲線,為此,去art庫檔案(在node_modules資料夾下)中查詢ART庫的引用,並且成功發現在react-native-art 繪圖入門中未介紹的path介面(S、C、Q、T有木有)。
3、既能畫二次貝塞爾,並且不用升級RN版本,這簡直是完美符合需求啊。
那麼使用方法就是
1)匯入ART庫
import React from 'react'; import { StyleSheet, View, ART } from 'react-native'; const {Surface, Shape, Path, Group} = ART;
2)給Path傳入二次貝塞爾曲線控制路徑,並在render中呼叫即可
render() { //this.console("render===speedStr:" + this.state.speedStr);
//const _path = new Path(this.state.speedStr).close();return ( <View style={Styles.canvasWrap}> <Surface width={w}height={h}> <Shape d={_path}stroke="#36ffff" strokeWidth={2}fill="rgba(54,255,255,0.2)"/> </Surface> </View> );}const _path = new Path('M0 0 Q5 20, 10 20 T15 35, Q17.5 50, 20 50 T25 25, Q27.5 0, 30 0 T35 0, Q37.5 0, 40 0 T45 15, Q47.5 30, 50 30 T55 20, Q57.5 10, 60 10 T65 5, Q67.5 0, 70 0').close();
4、以下為專案程式碼,可以直接引用
speedCanvas.js
/**
* Created by DELL on 2016/12/13.
*/
'use strict';
import React from 'react';
import {
StyleSheet,
View,
ART
} from 'react-native';
const {Surface, Shape, Path, Group} = ART;
import Dimensions from 'Dimensions';
const ScreenWidth = Dimensions.get('window').width;
const ScreenHeight = Dimensions.get('window').height;
const w = ScreenWidth;
const h = Math.ceil(ScreenHeight * 0.2);
const curvature = 2;//二次貝塞爾曲線曲率控制引數
const step = 20;//一次推進10距離單位
const stepNum = Math.floor(w / step);//螢幕寬度可容納幾個速率峰值的顯式
let speedCount = 300;
let speedCountHandle = -1;
const debugMsg = true;
//T只需要一個座標,其控制點已由前面的Q的控制點控制(控制方式為對稱控制,比如Q5 20, 10 20 T15 35,相當於Q5 20, 10 20 T15 20,15 35)
//因此起點座標(0,0)Q終點座標(10,20)與T座標(15,35)組成一條二次平滑貝塞爾曲線,
//(平滑的意思是Q終點座標並不是作為下一條貝塞爾曲線的起點,而是通過T座標使Q終點座標再次延伸一點至T座標,構成貝塞爾曲線的順滑結尾,並以T座標為下一條貝塞爾曲線的起點座標)
//Q終點座標的控制點座標的獲取方案為:取起點座標與Q終點座標的X軸座標的中點為X,取Q終點座標的Y軸座標為Y
//T座標的獲取方案為:取相鄰兩個Q終點座標的X軸座標與Y軸座標的終點座標為X和Y
//例如:const _path = new Path("M0 0 Q5 20, 10 20 T15 35, Q17.5 50, 20 50 T25 25, Q27.5 0, 30 0 T35 0, Q37.5 0, 40 0 T45 15, Q47.5 30, 50 30 T55 20, Q57.5 10, 60 10 T65 5, Q67.5 0, 70 0");
var speedCanvas = React.createClass({
getDefaultProps(){
return ({
speed: 0
});
},
getInitialState(){
return ({
speedLevel: 1,//速率檔位 1檔(0-h) 2檔(h-2h) 3檔(2h-3h) 4檔(3h-4h) 5檔(4h-5h)... h一般為100多
speedStr: ' ',
speedArr: []//[[10,20,[5,20],[15,35]],[20,50,[17.5,50],[25,25]],[30,0,[27.5,0],[35,0]],[40,0,[37.5,0],[45,15]],[50,30,[47.5,30],[55,20]],[60,10,[57.5,10],[65,5]],[70,0,[67.5,0],[72.5,0]]] 第一個為座標,第二個為速率,第三個為Q控制點座標,第四個為T座標
})
},
componentDidMount(){
},
componentWillReceiveProps(props){
clearTimeout(speedCountHandle);
speedCountHandle = setTimeout(()=> {
this.receiveSpeed({speed: props.speed});
}, speedCount);//此處定時器用於清除頻繁的state狀態改變而導致的頻繁畫線
},
receiveSpeed(props){
this.console("receiveSpeed===currSpeed:" + props.speed);
//保證最新的速率曲線在陣列的第一位
let _currLength = this.state.speedArr.length;
let _speedLevel = 1;
this.state.speedLevel = 1;//若不重置此值,則speedLevel記錄最高檔,速率曲線圖不會隨著檔位的下降而自動以該檔位的最高速率填滿畫布
if (_currLength < stepNum) {
this.state.speedArr.splice(0, 0, [10, props.speed]);
_currLength = this.state.speedArr.length;
for (let i = 0; i < _currLength; i++) {
this.state.speedArr[i][0] = (i + 1) * step;//重置X軸座標為10,20,30...
_speedLevel = Math.ceil(this.state.speedArr[i][1] / h);
_speedLevel > this.state.speedLevel ? this.state.speedLevel = _speedLevel : null;
}
this.checkSpeedArr();
}
else {
this.state.speedArr.splice(_currLength - 1, 1);//清除陣列最末元素,也即最舊的速率值
this.state.speedArr.splice(0, 0, [10, props.speed]);//往陣列首元素中插入最新速率值
_currLength = this.state.speedArr.length;
for (let i = 0; i < _currLength; i++) {
this.state.speedArr[i][0] = (i + 1) * step;//重置X軸座標為10,20,30...
_speedLevel = Math.ceil(this.state.speedArr[i][1] / h);
_speedLevel > this.state.speedLevel ? this.state.speedLevel = _speedLevel : null;
}
this.checkSpeedArr();
}
},
//確定各個速率點以及各速率點的Q、T點
checkSpeedArr(){
let _speedArr = this.state.speedArr;
for (let i = 0, j = _speedArr.length; i < j; i++) {
if (i > 0) {
_speedArr[i].length > 2 ? _speedArr[i].splice(2) : null;
_speedArr[i].push([_speedArr[i - 1][3][0] + (_speedArr[i][0] - _speedArr[i - 1][3][0]) / curvature, _speedArr[i][1]]);//添加當前座標的控制點(Q座標的控制點)
if (_speedArr[i + 1] !== undefined) {
_speedArr[i].push([_speedArr[i][0] + (_speedArr[i + 1][0] - _speedArr[i][0]) / curvature * (curvature - 1), _speedArr[i][1] + (_speedArr[i + 1][1] - _speedArr[i][1]) / 2]);//新增T座標點
}
else {
_speedArr[i].push([_speedArr[i][0] + (_speedArr[i][0] - _speedArr[i][2][0]), 0]);//新增T座標點,當其為最後一個座標點時候,需要與X軸閉合
}
}
else {
_speedArr[i].push([_speedArr[i][0] / curvature, _speedArr[i][1]]);//添加當前座標的控制點(Q座標的控制點)
if (_speedArr[i + 1] !== undefined) {
_speedArr[i].push([_speedArr[i][0] + (_speedArr[i + 1][0] - _speedArr[i][0]) / curvature * (curvature - 1), _speedArr[i][1] + (_speedArr[i + 1][1] - _speedArr[i][1]) / 2]);//新增T座標點
}
else {
_speedArr[i].push([_speedArr[i][0] + (_speedArr[i][0] - _speedArr[i][2][0]), 0]);//新增T座標點,當其為最後一個座標點時候,需要與X軸閉合
}
}
}
this.checkSpeedStr();
},
//右下角座標系的轉換,以右下角為座標系統的對映方式為:(0,0)=>(w,h) (5,10)=>(w-5,h-10)
checkSpeedStr(){
this.console("checkSpeedStr===speedLevel:" + this.state.speedLevel);
let _str = "M" + w + " " + h + " ";
let _speedArr = [].concat(JSON.parse(JSON.stringify(this.state.speedArr)));//拷貝一下陣列,用於將座標系轉換成右下角座標系
let _speedLevel = this.state.speedLevel;
for (let i = 0, j = _speedArr.length; i < j; i++) {
_str += "Q" + (w - _speedArr[i][2][0]) + " " + (h - _speedArr[i][2][1] / _speedLevel) + ", " + (w - _speedArr[i][0]) + " " + (h - _speedArr[i][1] / _speedLevel);
if (_speedArr[i][3] !== undefined) {
_str += " T" + (w - _speedArr[i][3][0]) + " " + (h - _speedArr[i][3][1] / _speedLevel) + ", ";
}
}
this.setState({speedStr: _str});
},
render() {
//this.console("render===speedStr:" + this.state.speedStr);
const _path = new Path(this.state.speedStr).close();
return (
<View style={Styles.canvasWrap}>
<Surface width={w} height={h}>
<Shape d={_path} stroke="#36ffff" strokeWidth={2} fill="rgba(54,255,255,0.2)"/>
</Surface>
</View>
);
},
console(msg){
debugMsg ? console.log("+++speedCanvas===" + msg + "===console end+++") : null;
}
});
var Styles = StyleSheet.create({
canvasWrap: {
width: w,
height: h,
borderBottomWidth: 2,
borderBottomColor: '#36ffff'
}
});
module.exports = speedCanvas;1)匯入該speedCanvas.js檔案,注意用大寫字母開頭以用作該js檔案的引用(否則會報引用型別的錯誤,大致好象是,需要一個類,但卻是一個數組物件之類的錯誤),比如
import SpeedCanvas from "./speedCanvas";
2)在render中引入,並傳入速率值作為屬性
<SpeedCanvas speed={this.state.speed} />
相關推薦
react-native-art畫二次貝塞爾曲線實現
1、關於react-native ART庫的使用,目前網上能搜到的少之又少,簡書上的一篇react-native-art 繪圖入門,從基本上講解了一下react-native-art的使用方法,但是隻是簡單的橫豎曲線的繪製,但專案中有一個需求就是繪製網速的速率曲線, (專案
微信小程式---通過二次貝塞爾曲線畫波浪
這兩週做一個新的專案,人員比較緊張,除了需求和UI,前端後端一個人來幹。 在專案需求確定後,UI隔了幾天設計出了UI介面,拿到UI效果圖後見有一個介面有波浪效果的我當時就蒙圈了,這都啥玩意啊?轉念想到了最近在IT圈挺火的那個事件:產品要求安卓程式設計師實現根據使用者手機殼顏
canvas 繪制二次貝塞爾曲線
logs text lineto quad img utf 技術分享 bsp element 代碼: <!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF-8
【原創】《矩陣的史詩級玩法》連載十九:用基向量矩陣實現二次貝塞爾曲線到標準拋物線的轉換
在講解磚塊鋪貼的時候,我們先用基礎的旋轉縮放等變換組合出了45度地圖鋪貼的變換矩陣。然後發現針對性太強,換成別的角度就很不好算了。接著改成了用基向量進行推導的方法。 然後到二元二次方程,雖然我們可以通過旋轉的方法消滅掉xy項從而判斷出方程對應的曲線型別,但過程過於繁瑣,
【原創】《矩陣的史詩級玩法》連載二十一:用矩陣計算直線和二次貝塞爾曲線的交點
搞了這麼多理論,現在是時候展現一下矩陣的魅力了。看看經過矩陣變換後的曲線求交是何等的方便! 上篇說過,矩陣簡化的效果立竿見影,如同連載二的直線橢圓相交判斷一樣。 按我的套路,我是會先給出傳統的做法,然後再用矩陣的史詩級玩法將其擊敗,不過這次為了不讓大家看暈,我選擇把順序調
繪製多條平滑曲線(基於二次貝塞爾曲線)
繪製策略:在每兩對點之間,加入一個新點(中間點)放在這兩點的正中間。然後使用這些中間點作為起點和終點,而把最初的那些點(原始點)作為控制點。 之前使用二次貝塞爾曲線繪製兩點的策略是已知的兩點作為起始點和終點,然後求出這兩點的中點作為控制點來繪製,結果曲線的圓滑程度不符合
Path使用--二階貝塞爾曲線實現水波效果
上面這個效果是使用Path繪製二階貝塞爾曲線實現的;二階貝塞爾曲線涉及到三個點,起始點、拐點、終點,而拐點有決定著曲線的形狀;下面這張圖大致展示了二階貝塞爾曲線: A點是起始點,C點是終點,B點是拐點,當然根據繪製的需求,B是變動的,繪製出來的曲線也就
在 egret 中 利用 tween 實現 二次貝塞爾運動
這篇文章使用了一個 javascript 的小技巧,結合 egret.Tween ,實現了 貝塞爾曲線。 記錄如下. 在製作遊戲的過程中,經常有些需求要求我們實現一個二次貝塞爾曲線的運動,比如子彈的飛行軌跡之類的 那麼如何使用egret來實現這類需求呢?其實非常簡單,首先我
canvas 繪制三次貝塞爾曲線
png 繪制 ges nload 代碼 idt head mage src 代碼: <!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF-8">
可視化n次貝塞爾曲線及過程動畫演示--大寶劍
ike all AS 2個 pat title pre while todo 先拋一個動畫模擬的一個例子,吊一吊Xing趣(4次) 不夠強?再來一個 這樣子,滿足你。demo說明 git倉庫地址示例 我眼睛花,沒看懂,能暫停不了? 可以控制動畫暫停與繼續。(供大家清
【演算法】-003 三次貝塞爾曲線的交點
【演算法】-003 三次貝塞爾曲線的交點 最近在工作中遇到一個問題,想通過計算兩條三次貝塞爾曲線的交點位置。嘗試了列舉法之後覺得計算速度太慢,於是來找其他演算法。 文章目錄 【演算法】-003 三次貝塞爾曲線的交點 1、 列舉法求貝塞爾曲線交
三次貝塞爾曲線關於點與長度在C++中實現:
三階貝塞爾曲線只能計算近似解,由於使用時對長度的精度要求不高,因此用部落格 【Unity】貝塞爾曲線關於點、長度、切線計算在 Unity中的C#實現 中提供的C#方法改寫為C++的,只是替換了一個結構體,因為並不懂原文中的Vector3類的使用而已。 定義一個POINT結構體,用
OpenGL實現攝像機漫遊/三次貝塞爾曲線
通過openglAPI實現攝像機漫遊,以及觀察生成的貝塞爾曲面 #include "stdafx.h" #include <GL/glut.h> #include <stdlib.h> #include<iostream> using namesp
CSS3 三次貝塞爾曲線(cubic-bezier)及其應用
<!doctype html> <html lang="en"> <head> <meta charset="UTF-8" /> <title> css3圓形軌跡動畫 </title>
自定義控制元件之二階貝塞爾曲線方法詳解
前言:先膜拜一下啟艦大神,本想自己寫一篇關於貝塞爾曲線的文章,但無奈此大神寫的太6了 ,所以直接轉載 相關文章:《Android自定義控制元件三部曲文章索引》: http://blog.csdn.net/harvic880925/article/details/50995268從
C++ 生成三次貝塞爾曲線
// 三次貝塞爾.cpp : Defines the entry point for the console application. // #include "stdafx.h" #include <stdio.h> #include <iostr
穿過已知點畫平滑曲線(3次貝塞爾曲線)
Interpolation with Bezier Curves 貝塞爾插值 A very simple method of smoothing polygons 一種非常簡單的多邊形平滑方法 翻譯:唐風 之前 comp.graphic.algorithms 上有一個討論,是關於怎麼樣
貝塞爾曲線實現的購物車添加商品動畫效果
right map 繪制 開始 enter 監聽 idg 過程 protected 效果圖如下: 1.activity_main.xml <?xml version="1.0" encoding="utf-8"?> <RelativeLayout xm
unity 實現物體沿指定的平滑曲線移動(通過貝塞爾曲線實現)
在實際專案開發中,為了實現某種動畫或者特效,策劃都會要求讓物體實現沿編輯的軌跡進行移動,今天這裡就講一下如何讓物體沿可編輯的路線進行移動,這裡主要是通過貝塞爾曲線實現。 首先要了解貝塞爾曲線的基礎知識及原理,具體可參考改連結: 這裡的思路就是首先就是把關鍵節點儲存起來
自定義view,貝塞爾曲線實現水波紋效果的動畫
作為一名碼農,除了用基本的姿勢去搬磚,還應該get一些炫酷的技能,用高逼格的姿態去搬磚。而貝塞爾曲線無疑是炫酷技能之一。 簡介: Bézier curve(貝塞爾曲線)是應用於二維圖形應用程式的數學曲線。 曲線定義:起始點、終止點(也稱錨點)、控制點。通過調整控