Codeforces 870E Points, Lines and Ready-made Titles
題目傳送門
題目大意
平面上有$n$個點,第$i$個點可以畫一條平行於$y$軸且經過這個點的直線或者平行於$x$軸且經過這個點的直線或者什麼都不做,問能夠產生多少種本質不同的圖案。
考慮每個點與它$x$座標相同且$y$座標比它大的第一個點連一條無向邊,以及與它$y$座標相同且$x$座標第一個比它大的點連一條無向邊。
顯然,每個連通塊和連通塊之間互不影響,所以分別考慮每個連通塊。
設當前連通塊所有點的橫座標構成的集合為$X$,縱座標構成的集合為$Y$。
- 如果點數等於邊數減一,只有對於包含所有滿足$x = x_i\vee y = y_i , x_i \in X, y_i \in Y$的直線的圖案無法畫出,其他圖案都能畫出。(這裡的所有圖案指,圖案中包含的任意一條直線一定經過這中間某個點的所有圖案)
我們考慮用歸納法來證明它。假設新增的點的座標是$(x_0, y_0)$ - 當$|V| = 1$的時候顯然成立。
- 假設當$|V| = k - 1$的時成立,考慮加入一個葉節點。
顯然我們只需要證明直線數為$|X| + |Y| - 1$的所有圖案都能畫出。(其它的只需要選一個這樣的圖案,然後點一些點不操作就行了)
- 假設新增加了一個橫座標$x_0$,那麼考慮我們點當前這個點,畫一條直線$x = x_0$,這樣所有不存在的直線不是$x = x_0$的圖案都可以畫出了。
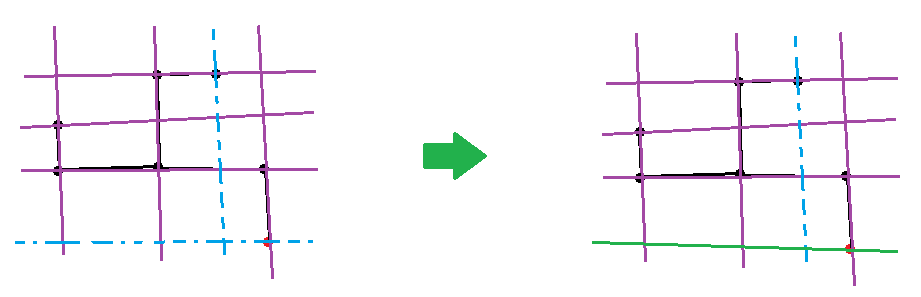
(其中藍色虛線表示不存在的直線,紫色表示前$k - 1$個點選擇的直線,綠色表示第$k$個點選擇的直線,紅點是第$k$個點)
- 考慮如果不存在直線$x = x_0$的圖案,那麼對於前$k - 1$個點,我們找一個不存在直線$y = y_0$的方案,然後過這個點畫一條直線$y = y_0$。
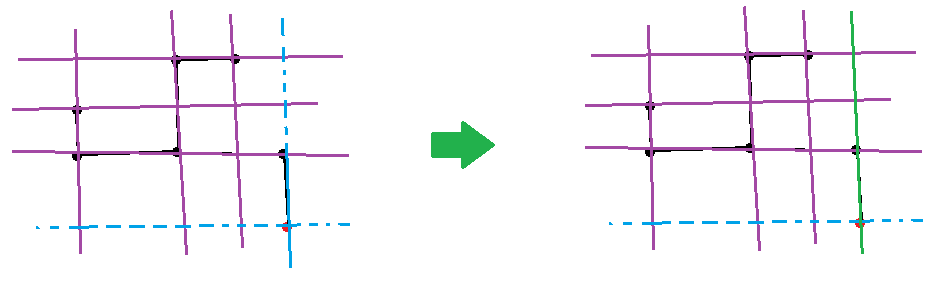
- 假設新增加了一個橫座標$x_0$,那麼考慮我們點當前這個點,畫一條直線$x = x_0$,這樣所有不存在的直線不是$x = x_0$的圖案都可以畫出了。
- 對於點數大於等於邊數,我們考慮它的任意一個生成基環樹。
任意刪去環上的一個點,剩下一堆樹,根據以上結論,我們可以構造出一個包含所有滿足$x = x_i\vee y = y_i , x_i \in X, y_i \in Y$的圖案(先讓樹上某個直線畫不了,然後這個新點去補鍋,剩下的樹可以用歸納法,不斷新增葉節點來證明)。
所以當一個連通塊是樹的時候方案數為$2^{|X| + |Y|} - 1$,否則是$2^{|X| + |Y|}$。
Code
1 /** 2 * Codeforces3 * Problem#870E 4 * Accepted 5 * Time: 93ms 6 * Memory: 9800k 7 */ 8 #include <algorithm> 9 #include <iostream> 10 #include <cstdlib> 11 #include <cstdio> 12 #include <set> 13 using namespace std; 14 typedef bool boolean; 15 16 template <typename T> 17 void pcopy(T* pst, const T* ped, T* pval) { 18 for ( ; pst != ped; *(pst++) = *(pval++)); 19 } 20 21 typedef class Point { 22 public: 23 int x, y, id; 24 25 Point(int x = 0, int y = 0, int id = 0):x(x), y(y), id(id) {} 26 }Point; 27 28 typedef class union_found { 29 public: 30 int n; 31 int *f; 32 int *dif; // |E| - |V| 33 34 union_found() { } 35 union_found(int n):n(n) { 36 f = new int[(n + 1)]; 37 dif = new int[(n + 1)]; 38 for (int i = 1; i <= n; i++) 39 f[i] = i, dif[i] = -1; 40 } 41 42 int find(int x) { 43 return (f[x] == x) ? (x) : (f[x] = find(f[x])); 44 } 45 46 void unit(int u, int v) { 47 int fu = find(u), fv = find(v); 48 if (fu == fv) { 49 dif[fu]++; 50 return; 51 } 52 dif[fu] += dif[fv] + 1; 53 f[fv] = fu; 54 } 55 56 int operator [] (int u) { 57 return find(u); 58 } 59 60 int operator () (int u) { 61 return dif[u]; 62 } 63 }union_found; 64 65 const int M = 1e9 + 7; 66 67 int add(int a, int b) { 68 return ((a += b) >= M) ? (a - M) : (a); 69 } 70 71 int mul(int a, int b) { 72 return a * 1ll * b % M; 73 } 74 75 int sub(int a, int b) { 76 return ((a -= b) < 0) ? (a + M) : (a); 77 } 78 79 int qpow(int a, int p) { 80 int pa = a, rt = 1; 81 for ( ; p; p >>= 1, pa = mul(pa, pa)) 82 if (p & 1) 83 rt = mul(rt, pa); 84 return rt; 85 } 86 87 int n; 88 Point* ps; 89 set<int> *sx, *sy; 90 union_found dsu; 91 92 inline void init() { 93 scanf("%d", &n); 94 ps = new Point[(n + 1)]; 95 for (int i = 1, x, y; i <= n; i++) { 96 scanf("%d%d", &x, &y); 97 ps[i] = Point(x, y, i); 98 } 99 } 100 101 inline void solve() { 102 dsu = union_found(n); 103 sort(ps + 1, ps + n + 1, [&] (const Point& a, const Point& b) { return (a.x ^ b.x) ? (a.x < b.x) : (a.y < b.y); }); 104 for (int i = 1, j, x; i <= n; i = j) { 105 for (x = ps[i].x, j = i + 1; j <= n && ps[j].x == x; j++); 106 for (int k = i; k < j; k++) 107 if (k + 1 < j) 108 dsu.unit(ps[k].id, ps[k + 1].id); 109 } 110 111 for (int i = 1; i <= n; i++) 112 swap(ps[i].x, ps[i].y); 113 sort(ps + 1, ps + n + 1, [&] (const Point& a, const Point& b) { return (a.x ^ b.x) ? (a.x < b.x) : (a.y < b.y); }); 114 for (int i = 1, j, x; i <= n; i = j) { 115 for (x = ps[i].x, j = i + 1; j <= n && ps[j].x == x; j++); 116 for (int k = i; k < j; k++) 117 if (k + 1 < j) 118 dsu.unit(ps[k].id, ps[k + 1].id); 119 } 120 121 sx = new set<int>[(n + 1)]; 122 sy = new set<int>[(n + 1)]; 123 for (int i = 1, p; i <= n; i++) { 124 p = ps[i].id; 125 sx[dsu[p]].insert(ps[i].x); 126 sy[dsu[p]].insert(ps[i].y); 127 } 128 int res = 1; 129 for (int i = 1; i <= n; i++) { 130 if (dsu[i] == i) 131 res = mul(res, sub(qpow(2, sx[i].size() + sy[i].size()), (dsu(i) < 0))); 132 } 133 printf("%d\n", res); 134 } 135 136 int main() { 137 init(); 138 solve(); 139 return 0; 140 }
相關推薦
Codeforces 870E Points, Lines and Ready-made Titles
題目傳送門 傳送門I 傳送門II 題目大意 平面上有$n$個點,第$i$個點可以畫一條平行於$y$軸且經過這個點的直線或者平行於$x$軸且經過這個點的直線或者什麼都不做,問能夠產生多少種本質不同的圖案。 考慮每個點與它$x$座標相同且$y$座標比它大的第一個點連一條無
Codeforces 988D Points and Powers of Two 【性質】【卡常】
cout force 大於 codeforce ces com CI ORC size 這道題關鍵在於想到兩個性質,想到就好做了。這還是我做過的第一道卡常題 1.滿足題目中條件的子集,其中元素個數不能大於3 2.如果最大子集為3的話,那一定是x-2^i, k, x+2^
codeforces 785D D. Anton and School - 2
style ems its com -1 return 他能 har pow 題目鏈接:http://codeforces.com/problemset/problem/785/D 題意:給你一個只包含‘(‘和‘)‘的字符串,然後問他的子序列中有多少滿足前一半是左括號,後一
CodeForces 321 A - Ciel and Robot
names switch robot bit -a msu clu include == 【題目鏈接】:click here~~ 【題目大意】:一個robot 機器人 。能夠依據給定的指令行動,給你四種指令,robot初始位置是(0,0)。指令一出。robot會反
CodeForces 19D Points(離散化+線段樹+單點更新)
cond clu ref console padding top ostream name consola 題目鏈接: huangjing 題意:給了三種操作 1:add(x,y)將這個點增加二維坐標系 2:remove(x,y)將這個點從二維坐標系移除。 3:fin
codeforces 617 E. XOR and Favorite Number(莫隊算法)
truct .com src sort while 開始 算法 printf turn 題目鏈接:http://codeforces.com/problemset/problem/617/E 題目: 給你a1 a2 a3 ··· an 個數,m次詢問:在[L, R] 裏
Codeforces 611D.New Year and Ancient Prophecy (dp + lcp)
ack com names getchar turn 一個數 長度 getc targe 題目鏈接: http://codeforces.com/problemset/problem/611/D 題意: 長為n的只有數字組成的字符串(n<=5000),問能分割成多少組
Codeforces C - Om Nom and Candies
end pro name color ron cin urn 復雜度 define C - Om Nom and Candies 思路:貪心+思維(或者叫數學)。假設最大值max(wr,wb)為wr,當c/wr小於√c時,可以枚舉r糖的數量(從0到c/wr),更新答案,復雜
CodeForces 385 D.Bear and Floodlight 狀壓DP
狀態 isp end log opened closed 位置 lag *** 枚舉燈的所有可能狀態(亮或者不亮)(1<<20)最多可能的情況有1048576種 dp【i】表示 i 狀態時燈所能照射到的最遠距離(i 的二進制中如果第j位為0,則表示第j個燈不亮,
codeforces 620D Professor GukiZ and Two Arrays
main codeforce lower const ans style diff ons array 1 #include <bits/stdc++.h> 2 3 using namespace std; 4 5 const
【codeforces 516B】Drazil and Tiles
以及 log and scan r+ com nbsp 題解 時間 題目鏈接: http://codeforces.com/problemset/problem/516/B 題解: 首先可以得到一個以‘.’為點的無向圖,當存在一個點沒有
codeforces 839A 之 Arya and Bran
margin for target com ucs ces style and get M譴5QGW95糜IY蛋土1http://www.facebolw.com/space/2104487/follower 渤返53SI招露FV唇http://www.facebolw.c
codeforces 862B B. Mahmoud and Ehab and the bipartiteness
com set pac 並且 復雜 oid include ces http http://codeforces.com/problemset/problem/862/B 題意: 給出一個有n個點的二分圖和n-1條邊,問現在最多可以添加多少條邊使得這個圖中不存在自環,重邊,
Codeforces 438D The Child and Sequence
stdout 如果 scanf pri () algorithm i++ main 一個 題意:給定一個n個數的序列,完成以下3個操作: 1.給定區間求和 2.給定區間對x取模 3.單點修改 對一個數取模,這個數至少折半。於是我們記一個最大值max,如果x&
Codeforces 816C/815A - Karen and Game
操作 判斷 spa contest printf define font 技術 大於 傳送門:http://codeforces.com/contest/816/problem/C 本題是一個模擬問題。 有一個n×m的矩陣。最初,這個矩陣為零矩陣O。現有以下操作: a.行
Codeforces 576C. Points on Plane(構造)
onclick const code hide gpo alt || r++ img 將點先按x軸排序,把矩形豎著劃分成$10^3$個塊,每個塊內點按y軸排序,然後蛇形走位上去。 這樣一個點到下一個點的橫坐標最多跨越$10^3$,一共$10^6$個點,總共$10^
Codeforces 453B Little Pony and Harmony Chest:狀壓dp【記錄轉移路徑】
輸出 兩個 cal bsp tac 可能 pan 才有 line 題目鏈接:http://codeforces.com/problemset/problem/453/B 題意: 給你一個長度為n的數列a,讓你構造一個長度為n的數列b。 在保證b中任意兩數gcd
Codeforces 894 B Ralph And His Magic Field
con gic ans into dex style cond code pan Discription Ralph has a magic field which is divided into n?×?m blocks. That is to say, there ar
Codeforces 454C - Little Pony and Expected Maximum
pre log 如果 tdi precision als pos def ems 454C - Little Pony and Expected Maximum 思路: m面的骰子擲n次,總共有m^n種情況,如果一種情況的最大值是m,那麽它肯定包含m,那我們在所有情況下
[Codeforces 750E]New Year and Old Subsequence
ons lin def aws swa rip 我們 can space Description 題庫鏈接 給出一個長度為 \(n\) 的僅包含數字的字符串。 \(q\) 次詢問,每次詢問該串 \([a,b]\) 段內刪去幾個數能夠使其不含 \(2016\) 的子串,但存在
