在求解區間第k個數的問題，除了劃分樹以外我們還可以使用另一種高效的方法 ------ 歸併樹。

1、演算法描述

        所謂歸併樹，就是利用線段樹的建樹過程，將歸併排序的過程儲存。(不會線段樹：here，不會歸併排序：here)。在說明歸併樹之前我們先看看這樣的一個問題：

給定一個序列A[1...n]，現在對該序列能夠進行一個操作：Query(left, right, k):表示查詢區間[left, right]的第k大樹。一共進行m次的查詢，要求你儘可能快的實現該操作

        一看到這個問題，我們可以立馬得到一個樸素的演算法：每次對區間[left, right]進行從小到大排序，直接輸出第k大的值。我們稍稍分析一下這種樸素的演算法所需的時間複雜度。首先每次對區間[left, right]進行排序所需的時間為O(nlogn)。一共進行m次查詢，那麼其總的時間複雜度為O(mnlogn)。第一眼看上去感覺這個演算法貌似還不錯，仔細分析就能發現，一旦m和n同時很大，那麼這個演算法就會很慢。那麼此時，我們應該思考有麼有更快的演算法。顯然是有的，他就是今天我們要講的歸併樹(當然還有其他方法，下次再介紹)。

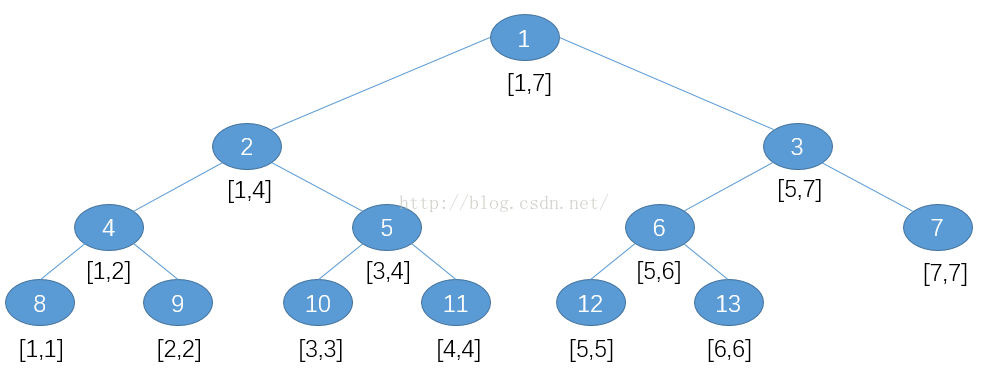
         歸併樹簡單來說就是線段樹加歸併排序，那麼他們是怎麼結合在一起的呢？假定現在A[1...7] = {7,6,....,1},我們先看看這個該序列歸併排序的過程把:

        我們在文章前也提到我們是利用線段樹的儲存結構來儲存歸併排序的過程，所以我們對照的看一下線段樹的結構：

        這麼一對比我們會發現線段樹的儲存結構與歸併排序的過程高度的一致，於是我們將兩者合併：

        通過上邊的分析，我們不難得出歸併樹的建樹過程，程式碼如下：

#define MAXN (1<<18)
#define DEEP 20
//sorted用來儲存歸併樹的樹體，a為輸入序列
int sorted[DEEP][MAXN], a[MAXN];
void build(int deep, int lft, int rht){
    if(lft == rht){
        sorted[deep][lft] = a[lft];
        return ;
    }
    int mid = (lft + rht) >> 1;
    build(deep+1, lft, mid);
    build(deep+1, mid+1, rht);
    //進行歸併
    int i = lft, j = mid+1, k = lft;
    while(i <= mid && j <= rht){
        if(sorted[deep+1][i] <= sorted[deep+1][j])
            sorted[deep][k++] = sorted[deep+1][i++];
        else sorted[deep][k++] = sorted[deep+1][j++];
    }
    while(i <= mid) sorted[deep][k++] = sorted[deep+1][i++];
    while(j <= rht) sorted[deep][k++] = sorted[deep+1][j++];
}
 

        通過程式碼我們發現，歸併樹採用層狀結構了。原因很簡單，因為要將歸併排序的整個過程完完整整的儲存下來，使用以前的樹狀結構顯然不能滿足。因為此時每一層都具有n個元素。現在我們已經完成了建樹的工作，現在還有一個大問題就是查詢。那麼我們應該怎麼查呢?一個區間的第k個數就是答案嗎？只要稍微一思考就能發現這個思路不對。其實這時候我們可以使用一個比較“笨”的方法 --- 試一下唄。那麼怎麼試呢？我們用可以把[1,n]區間內的所有數都帶入區間[left,right]中，看看那個數滿足是這個區間的第k大數。顯然我們這麼做的話，我們可能會得到很多個數，假定我們從[1,n]區間內找到了n1個數且按照從小到大的順序儲存在key[n1]陣列中。

        那麼此時我們怎麼確定這n1個數，哪一個在區間[left,right]之中呢？一眼望去好像沒什麼方法貌似。那麼作為笨的人，我們就採用一種比較笨的方法吧。假設x為區間內的第k大的數從key[n1]內任取一個數y。那麼我們分類討論：

        ①當y > x時，如果存在這種情況，那麼y為區間[left,right]內第k+1大的數，顯然y不可能出現在這n1個數。

        ②當y <= x時，這時候y都滿足情況，那麼根據①的分析，我們可以發現x是這n1個數中最大的那一個。

        綜上所述，當區間[1,n]內有多個數滿足為區間[left,right]的第k大數時，值最大的那一個為目標值，即區間的第k大數。

        經過上述分析，我們可以得到如下的程式碼：

//查詢小於key的個數
//[qlft,qrht]為查詢區間
//[lft, rht]為歸併樹上的區間
int query(int deep, int lft, int rht, int qlft, int qrht, int key){
    if(qrht < lft || qlft > rht) return 0;
    if(qlft <= lft && rht <= qrht)
        return std::lower_bound(&sorted[deep][lft], &sorted[deep][rht]+1, key) - &sorted[deep][lft];
    int mid = (lft + rht) >> 1;
    return query(deep+1, lft, mid, qlft, qrht, key) + query(deep+1, mid+1, rht, qlft, qrht, key);
}
//二分查詢在區間[qlft, qrht]上滿足是第k大的數
//換而言之，即滿足和比key小的有k個數的key
int solve(int n, int qlft, int qrht, int k){
	int low = 0, high = n;
	while(low+1 < high){
		int mid= (low + high) >> 1;
		//cnt 為小於 sorted[0][mid]的個數
		int cnt = query(0, 0, n-1, qlft, qrht, sorted[0][mid]);
		if(cnt <= k) low = mid; //[mid, high)
		else high = mid; //[low, mid)
	}
	return sorted[0][low];
}

2、時間複雜度

        通過上述程式碼我們可以發現，影響歸併樹的時間複雜度的地方只有兩處①建樹②查詢。且這兩處的時間複雜度相互獨立。我們先分析建樹過程的時間複雜度吧，每一層都對n個數進行了操作，一用logn + 1層。於是建樹的時間複雜度為O(nlogn)。我們再分析每一次查詢操作的時間複雜度，①二分的對[1,n]內的數進行試，找出滿足第k大的數②遞迴的對歸併樹上的區間進行進行查詢③在每一個區間上查詢比key小的元素個數。於是我們可以發現我們一共進行上次操作且每一次操作均為logn，故時間複雜度為O(logn*logn*logn)。一共進行m次查詢那麼總的時間複雜度為O(m*logn*logn*logn)。故歸併樹的最終時間複雜度為O(max(n*logn, m*logn*logn*logn))。

        文章的最後，附上一道模板題POJ2104K-th Number。最後的最後附上解題程式碼，如下：

#include <cstdio>
#include <algorithm>
#define MAXN (100000)
#define DEEP (20)
using namespace std;
int sorted[DEEP][MAXN], a[MAXN];
void build(int deep, int lft, int rht){
    if(lft == rht){
        sorted[deep][lft] = a[lft];
        return ;
    }
    int mid = (lft + rht) >> 1;
    build(deep+1, lft, mid);
    build(deep+1, mid+1, rht);
    int p = lft, q = mid+1, k = lft;
    while(p <= mid && q <= rht){
        if(sorted[deep+1][p] <= sorted[deep+1][q])
            sorted[deep][k++] = sorted[deep+1][p++];
        else sorted[deep][k++] = sorted[deep+1][q++];
    }
    while(p <= mid) sorted[deep][k++] = sorted[deep+1][p++];
    while(q <= rht) sorted[deep][k++] = sorted[deep+1][q++];
}
int query(int deep, int lft, int rht, int qlft, int qrht, int key){
    if(qrht < lft || qlft > rht) return 0;
    if(qlft <= lft && rht <= qrht)
        return lower_bound(&sorted[deep][lft], &sorted[deep][rht]+1, key) - &sorted[deep][lft];
    int mid = (lft + rht) >> 1;
    return query(deep+1, lft, mid, qlft, qrht, key) + query(deep+1, mid+1, rht, qlft, qrht, key);
}
int solve(int n, int qlft, int qrht, int k){
	int low = 1, high = n+1;
	while(low+1 < high){
		int mid= (low + high) >> 1;
		int cnt = query(0, 1, n, qlft, qrht, sorted[0][mid]);
		if(cnt <= k) low = mid;
		else high = mid;
	}
	return sorted[0][low];
}
int main(){
    int n, m;
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i++){
        scanf("%d", &a[i]);
    }
    build(0, 1, n);
    while(m--){
        int qlft, qrht, k;
        scanf("%d%d%d", &qlft, &qrht, &k);
        printf("%d\n", solve(n, qlft, qrht, k-1));
    }
    return 0;
}