poj 2104 K-th Number 主席樹+超級詳細解釋
阿新 • • 發佈:2019-02-15
題目大意:給出一段數列,讓你求[L,R]區間內第幾大的數字!
在這裡先介紹一下主席樹!
如果想了解什麼是主席樹,就先要知道線段樹,主席樹就是n棵線段樹,因為線段樹只能維護最大值或者最小值,要想求出第二大的數字怎麼辦呢?兩顆線段樹唄!好,那麼第n大呢,就可以構造n棵線段樹,這樣的記憶體是顯然會爆掉的,那麼怎麼辦呢?因為每一次更新都是更新的是從葉子節點到根節點的一條路,路的長度大約是
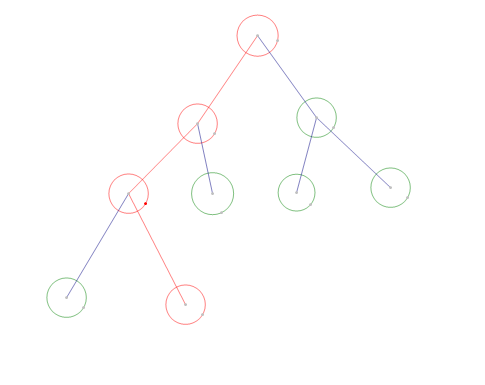
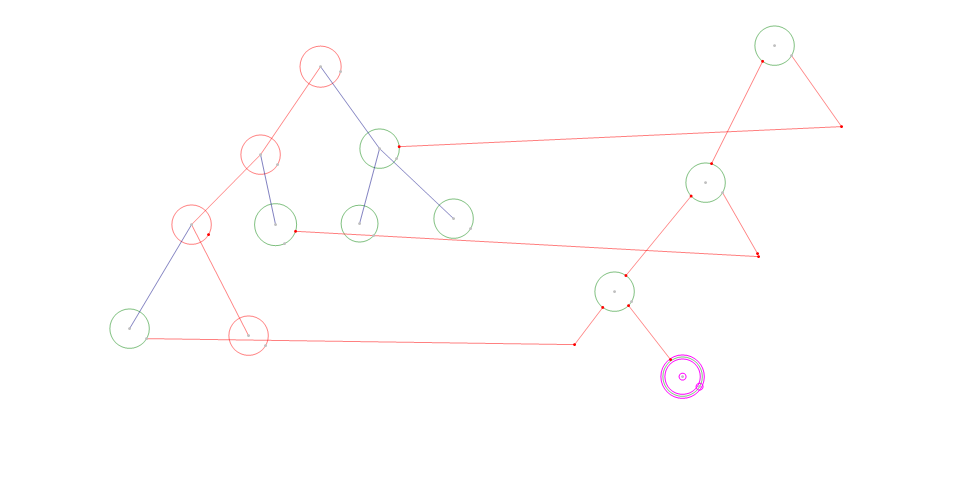
當進行更新操作的時候,也就是新建一個線段樹,但是這可線段樹不會全部都建立起來,只把修改的節點建立一下就可以,如果節點不修改就可以用以前線段樹的節點指向當前新建的線段樹的節點,先看下圖然後在解釋:
對於沒有修改的節點就直接指向新建的線段樹就可以了!
對於每一棵線段樹都是類似於下圖的樣子的:
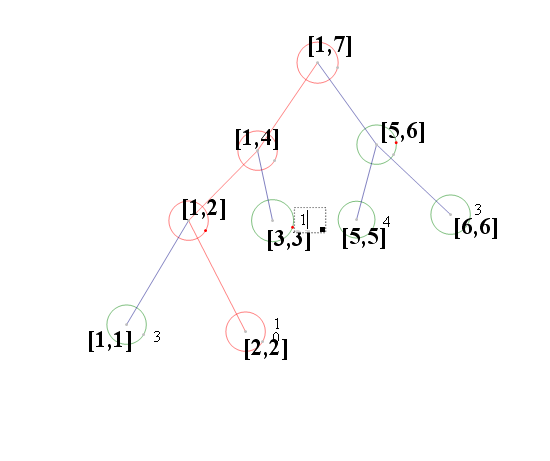
這棵樹表示數字1出現了三次,數字2出現了1次,數字三出現了一次,數字五出現了4次,數字6出現了三次;
用一個數組來表示就是
sum[i]=j表示數字i出現了j次。 這樣在通過一般線段樹的
pushdown操作就變為了我們熟悉的線段樹了!如下圖: 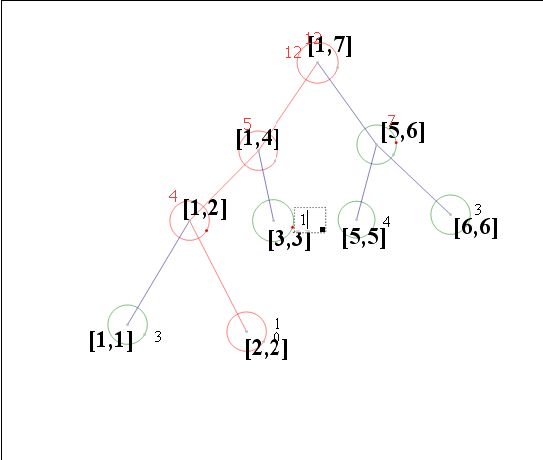
下面據一個例子[1,1,2,1,5,5,5,5,6,6,6,3]解釋一下建立線段樹的全部過程:
首先是一棵空的線段樹
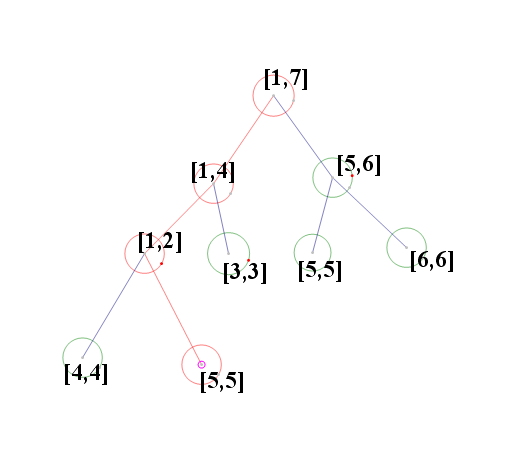
順序的由第一個元素開始進入線段樹並且開始更新:
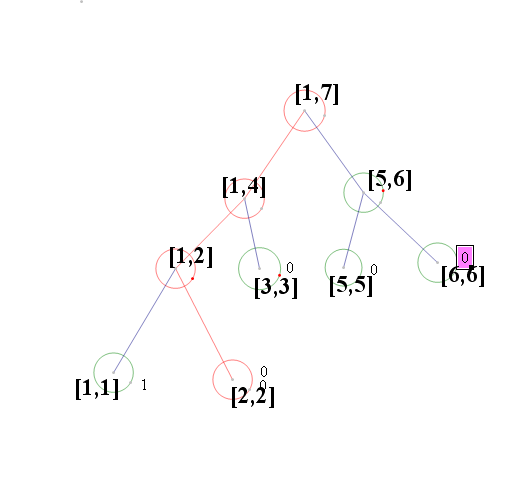

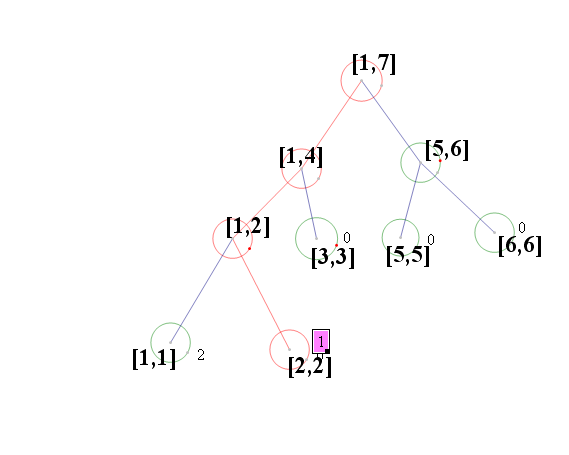
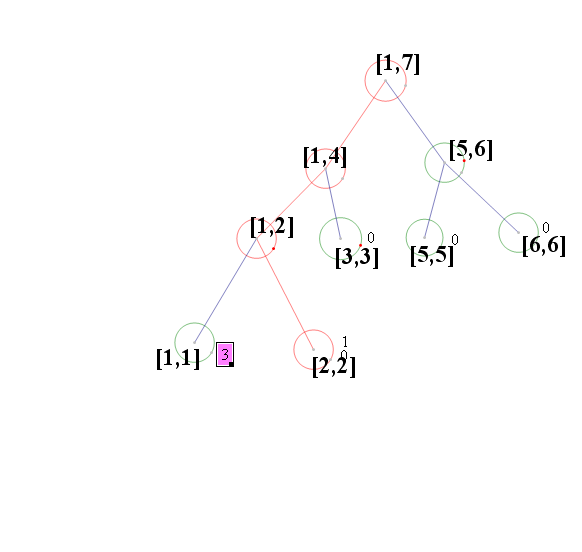
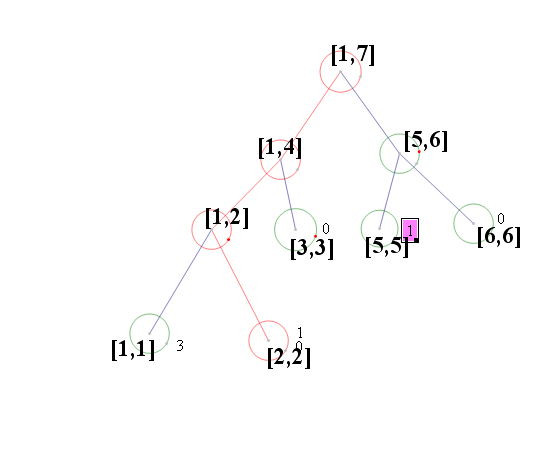
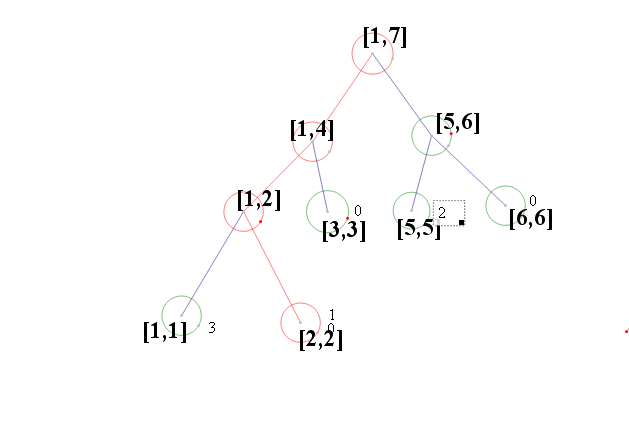
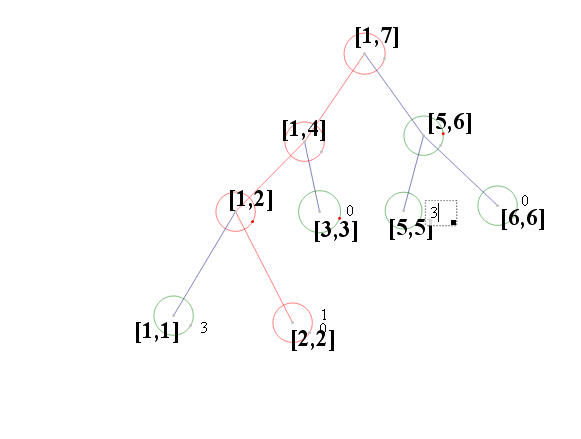

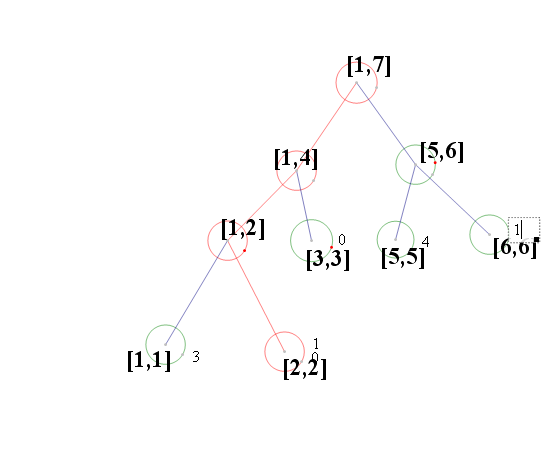
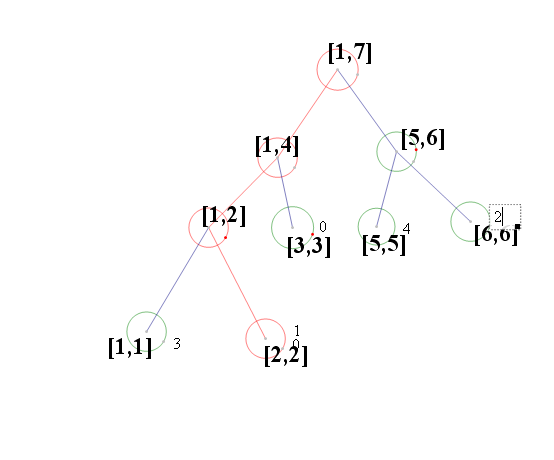
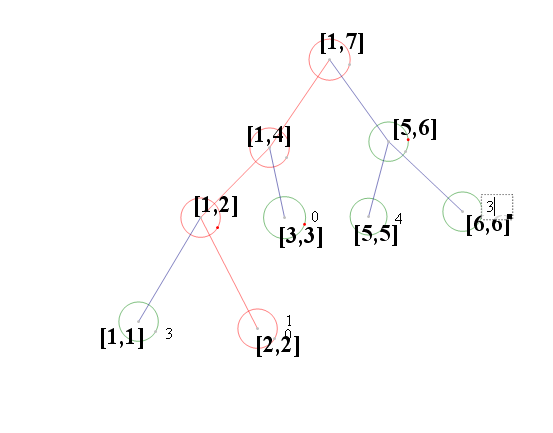
這樣我們就可以知道不同狀態下的線段樹了,比如sum[i]當前節點對應的數字出現了幾次,對於 L,R]
這個基於的原理舉個例子就知道了我們知道區間[1,3,3,4,5]區間一共有5個元素那麼第5大的就是最後一個元素了!
AC程式碼
#include <cstdio>
#include <cstring>
#include <iostream>
#include <vector>
#include <algorithm>
using namespace