零基礎入門深度學習(6)
在上一篇文章《零基礎入門深度學習(4):迴圈神經網路》中,我們介紹了迴圈神經網路以及它的訓練演算法。我們也介紹了迴圈神經網路很難訓練的原因,這導致了它在實際應用中,很難處理長距離的依賴。在本文中,我們將介紹一種改進之後的迴圈神經網路:長短時記憶網路(Long Short Term Memory Network, LSTM),它成功地解決了原始迴圈神經網路的缺陷,成為當前最流行的RNN,在語音識別、圖片描述、自然語言處理等許多領域中成功應用。
但不幸的一面是,LSTM的結構很複雜,因此,我們需要花上一些力氣,才能把LSTM以及它的訓練演算法弄明白。在搞清楚LSTM之後,我們再介紹一種LSTM的變體:GRU (Gated Recurrent Unit)。 它的結構比LSTM簡單,而效果卻和LSTM一樣好,因此,它正在逐漸流行起來。最後,我們仍然會動手實現一個LSTM。
長短時記憶網路是啥
我們首先了解一下長短時記憶網路產生的背景。回顧一下《零基礎入門深度學習(4):迴圈神經網路》中推導的,誤差項沿時間反向傳播的公式:

梯度消失到底意味著什麼?在《零基礎入門深度學習(4):迴圈神經網路》中我們已證明,權重陣列W最終的梯度是各個時刻的梯度之和,即:
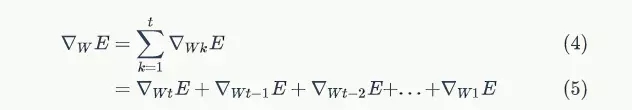
假設某輪訓練中,各時刻的梯度以及最終的梯度之和如下圖:

我們就可以看到,從上圖的t-3時刻開始,梯度已經幾乎減少到0了。那麼,從這個時刻開始再往之前走,得到的梯度(幾乎為零)就不會對最終的梯度值有任何貢獻,這就相當於無論t-3時刻之前的網路狀態h是什麼,在訓練中都不會對權重陣列W的更新產生影響,也就是網路事實上已經忽略了t-3時刻之前的狀態。這就是原始RNN無法處理長距離依賴的原因。
既然找到了問題的原因,那麼我們就能解決它。從問題的定位到解決,科學家們大概花了7、8年時間。終於有一天,Hochreiter和Schmidhuber兩位科學家發明出長短時記憶網路,一舉解決這個問題。
其實,長短時記憶網路的思路比較簡單。原始RNN的隱藏層只有一個狀態,即h,它對於短期的輸入非常敏感。那麼,假如我們再增加一個狀態,即c,讓它來儲存長期的狀態,那麼問題不就解決了麼?如下圖所示:
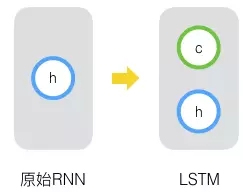
新增加的狀態c,稱為單元狀態(cell state)。我們把上圖按照時間維度展開:
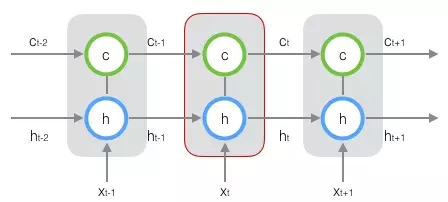

LSTM的關鍵,就是怎樣控制長期狀態c。在這裡,LSTM的思路是使用三個控制開關。第一個開關,負責控制繼續儲存長期狀態c;第二個開關,負責控制把即時狀態輸入到長期狀態c;第三個開關,負責控制是否把長期狀態c作為當前的LSTM的輸出。三個開關的作用如下圖所示:
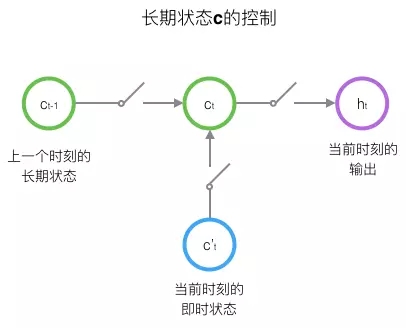
接下來,我們要描述一下,輸出h和單元狀態c的具體計算方法。
長短時記憶網路的前向計算
前面描述的開關是怎樣在演算法中實現的呢?這就用到了門(gate)的概念。門實際上就是一層全連線層,它的輸入是一個向量,輸出是一個0到1之間的實數向量。假設W是門的權重向量,是偏置項,那麼門可以表示為:

我們先來看一下遺忘門:

下圖顯示了遺忘門的計算:
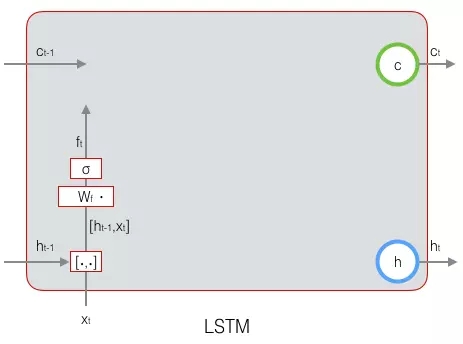
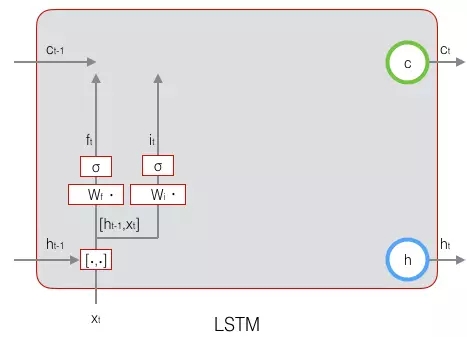
接下來看看輸入門:
上式中,Wi是輸入門的權重矩陣,bi是輸入門的偏置項。下圖表示了輸入門的計算:

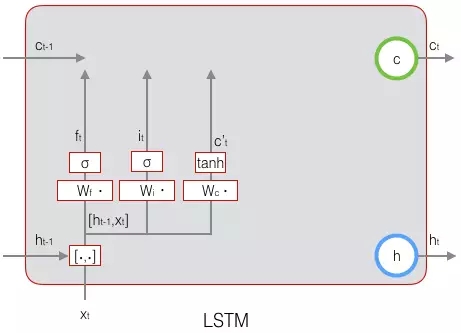


下圖表示輸出門的計算:
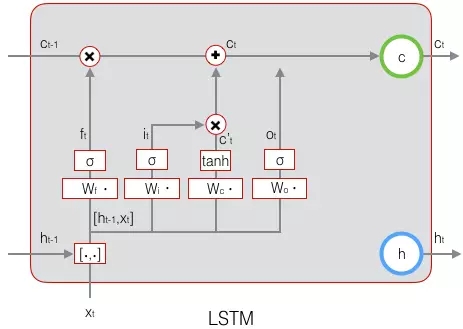
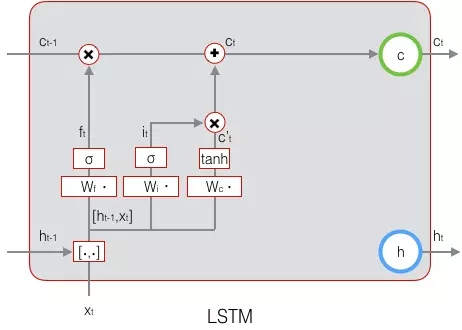
LSTM最終的輸出,是由輸出門和單元狀態共同確定的:
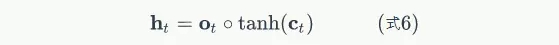
下圖表示LSTM最終輸出的計算:
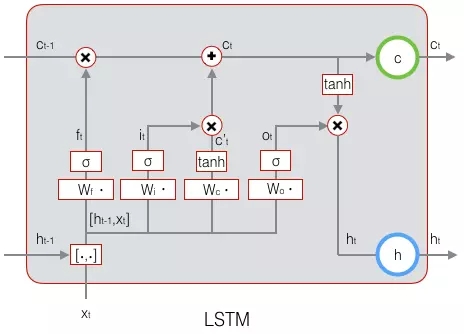
式1到式6就是LSTM前向計算的全部公式。至此,我們就把LSTM前向計算講完了。
長短時記憶網路的訓練
熟悉我們這個系列文章的同學都清楚,訓練部分往往比前向計算部分複雜多了。LSTM的前向計算都這麼複雜,那麼,可想而知,它的訓練演算法一定是非常非常複雜的。現在只有做幾次深呼吸,再一頭扎進公式海洋吧。
LSTM訓練演算法框架
LSTM的訓練演算法仍然是反向傳播演算法,對於這個演算法,我們已經非常熟悉了。主要有下面三個步驟:

關於公式和符號的說明
首先,我們對推導中用到的一些公式、符號做一下必要的說明。
接下來的推導中,我們設定gate的啟用函式為sigmoid函式,輸出的啟用函式為tanh函式。他們的導數分別為:
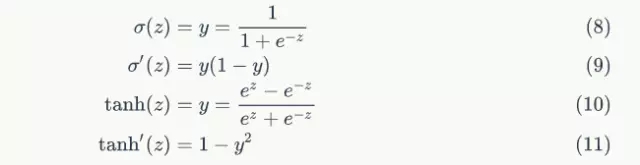
從上面可以看出,sigmoid和tanh函式的導數都是原函式的函式。這樣,我們一旦計算原函式的值,就可以用它來計算出導數的值。



誤差項沿時間的反向傳遞

下面,我們要把式7中的每個偏導數都求出來。根據式6,我們可以求出:

根據式4,我們可以求出:

因為:
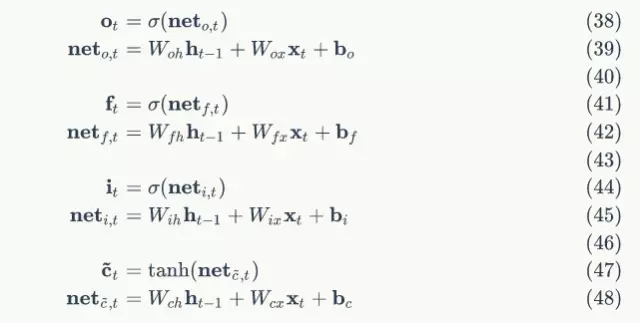
我們很容易得出:
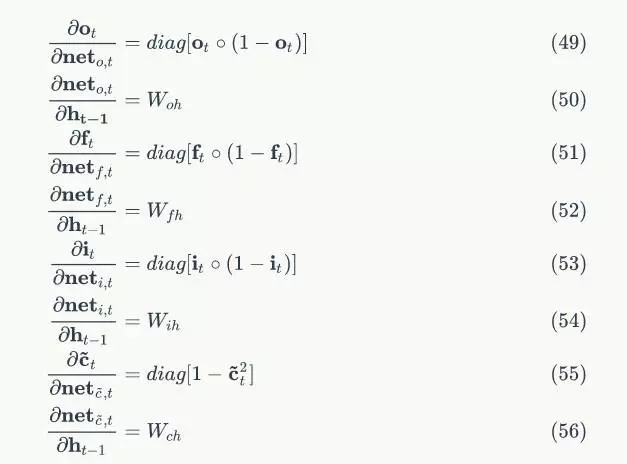
將上述偏導數帶入到式7,我們得到:
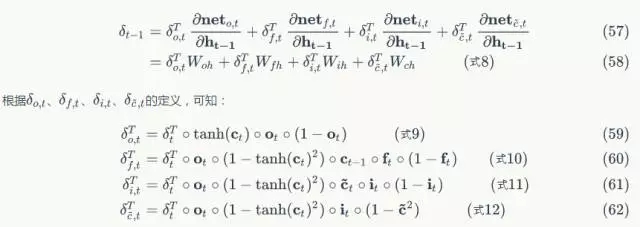
式8到式12就是將誤差沿時間反向傳播一個時刻的公式。有了它,我們可以寫出將誤差項向前傳遞到任意k時刻的公式:
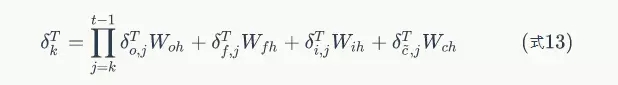
將誤差項傳遞到上一層
我們假設當前為第l層,定義l-1層的誤差項是誤差函式對l-1層加權輸入的導數,即:


式14就是將誤差傳遞到上一層的公式。
權重梯度的計算
對於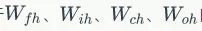 的權重梯度,我們知道它的梯度是各個時刻梯度之和(證明過程請參考文章《零基礎入門深度學習(4)
:迴圈神經網路》),我們首先求出它們在t時刻的梯度,然後再求出他們最終的梯度。
的權重梯度,我們知道它的梯度是各個時刻梯度之和(證明過程請參考文章《零基礎入門深度學習(4)
:迴圈神經網路》),我們首先求出它們在t時刻的梯度,然後再求出他們最終的梯度。
我們已經求得了誤差項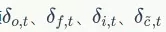 ,很容易求出t時刻的
,很容易求出t時刻的 :
:
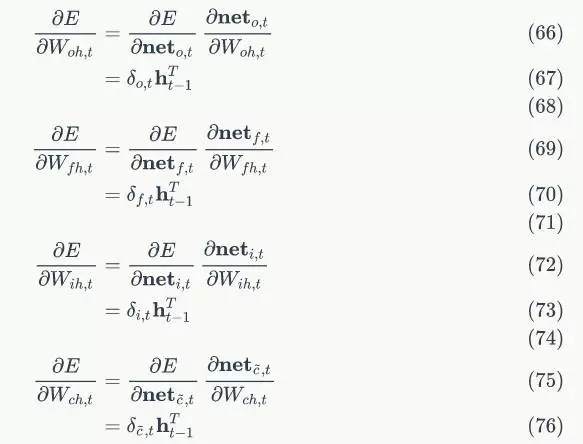
將各個時刻的梯度加在一起,就能得到最終的梯度:
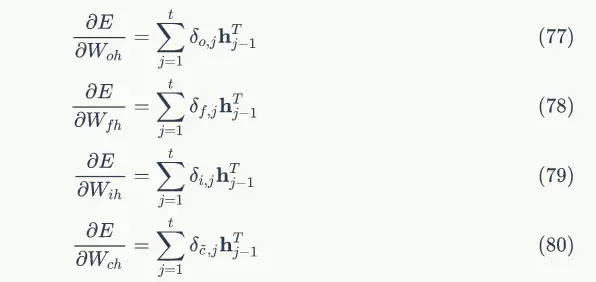
對於偏置項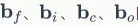 的梯度,也是將各個時刻的梯度加在一起。下面是各個時刻的偏置項梯度:
的梯度,也是將各個時刻的梯度加在一起。下面是各個時刻的偏置項梯度:
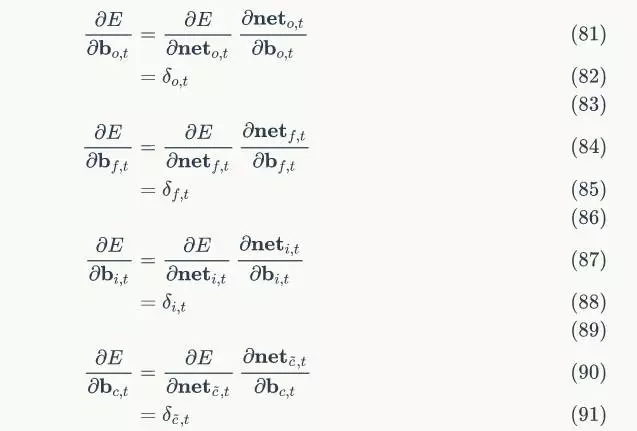
下面是最終的偏置項梯度,即將各個時刻的偏置項梯度加在一起:
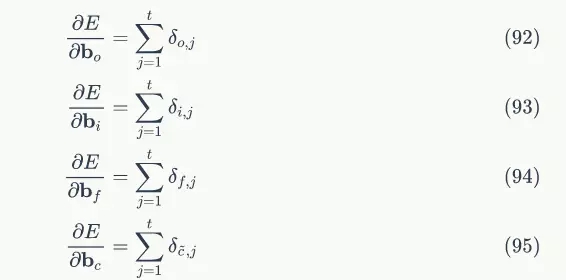
對於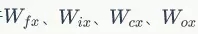 的權重梯度,只需要根據相應的誤差項直接計算即可:
的權重梯度,只需要根據相應的誤差項直接計算即可:
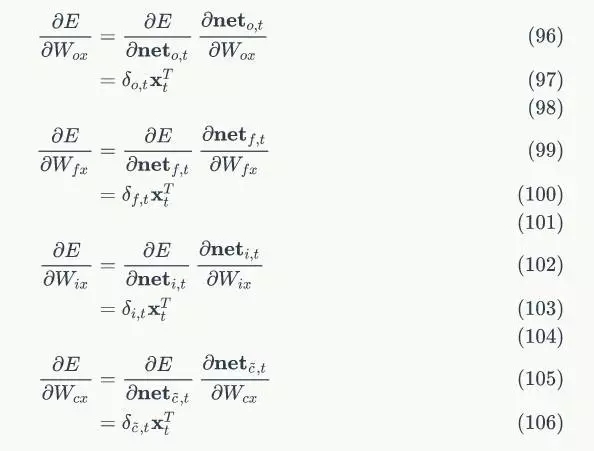
以上就是LSTM的訓練演算法的全部公式。因為這裡面存在很多重複的模式,仔細看看,會發覺並不是太複雜。
當然,LSTM存在著相當多的變體,讀者可以在網際網路上找到很多資料。因為大家已經熟悉了基本LSTM的演算法,因此理解這些變體比較容易,因此本文就不再贅述了。
長短時記憶網路的實現
在下面的實現中,LSTMLayer的引數包括輸入維度、輸出維度、隱藏層維度,單元狀態維度等於隱藏層維度。gate的啟用函式為sigmoid函式,輸出的啟用函式為tanh。
啟用函式的實現
我們先實現兩個啟用函式:sigmoid和tanh。
class SigmoidActivator(object):
def forward(self, weighted_input):
return 1.0 / (1.0 + np.exp(-weighted_input))
def backward(self, output):
return output * (1 - output)
class TanhActivator(object):
def forward(self, weighted_input):
return 2.0 / (1.0 + np.exp(-2 * weighted_input)) - 1.0
def backward(self, output):
return 1 - output * outputLSTM初始化
和前兩篇文章程式碼架構一樣,我們把LSTM的實現放在LstmLayer類中。
根據LSTM前向計算和方向傳播演算法,我們需要初始化一系列矩陣和向量。這些矩陣和向量有兩類用途,一類是用於儲存模型引數,例如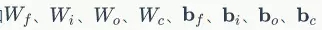 ;另一類是儲存各種中間計算結果,以便於反向傳播演算法使用,它們包括
;另一類是儲存各種中間計算結果,以便於反向傳播演算法使用,它們包括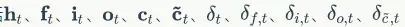 ,以及各個權重對應的梯度。
,以及各個權重對應的梯度。
在建構函式的初始化中,只初始化了與forward計算相關的變數,與backward相關的變數沒有初始化。這是因為構造LSTM物件的時候,我們還不知道它未來是用於訓練(既有forward又有backward)還是推理(只有forward)。
class LstmLayer(object):
def __init__(self, input_width, state_width,
learning_rate):
self.input_width = input_width
self.state_width = state_width
self.learning_rate = learning_rate
# 門的啟用函式
self.gate_activator = SigmoidActivator()
# 輸出的啟用函式
self.output_activator = TanhActivator()
# 當前時刻初始化為t0
self.times = 0
# 各個時刻的單元狀態向量c
self.c_list = self.init_state_vec()
# 各個時刻的輸出向量h
self.h_list = self.init_state_vec()
# 各個時刻的遺忘門f
self.f_list = self.init_state_vec()
# 各個時刻的輸入門i
self.i_list = self.init_state_vec()
# 各個時刻的輸出門o
self.o_list = self.init_state_vec()
# 各個時刻的即時狀態c~
self.ct_list = self.init_state_vec()
# 遺忘門權重矩陣Wfh, Wfx, 偏置項bf
self.Wfh, self.Wfx, self.bf = (
self.init_weight_mat())
# 輸入門權重矩陣Wfh, Wfx, 偏置項bf
self.Wih, self.Wix, self.bi = (
self.init_weight_mat())
# 輸出門權重矩陣Wfh, Wfx, 偏置項bf
self.Woh, self.Wox, self.bo = (
self.init_weight_mat())
# 單元狀態權重矩陣Wfh, Wfx, 偏置項bf
self.Wch, self.Wcx, self.bc = (
self.init_weight_mat())
def init_state_vec(self):
'''
初始化儲存狀態的向量
'''
state_vec_list = []
state_vec_list.append(np.zeros(
(self.state_width, 1)))
return state_vec_list
def init_weight_mat(self):
'''
初始化權重矩陣
'''
Wh = np.random.uniform(-1e-4, 1e-4,
(self.state_width, self.state_width))
Wx = np.random.uniform(-1e-4, 1e-4,
(self.state_width, self.input_width))
b = np.zeros((self.state_width, 1))
return Wh, Wx, b前向計算的實現
forward方法實現了LSTM的前向計算:
def forward(self, x):
'''
根據式1-式6進行前向計算
'''
self.times += 1
# 遺忘門
fg = self.calc_gate(x, self.Wfx, self.Wfh,
self.bf, self.gate_activator)
self.f_list.append(fg)
# 輸入門
ig = self.calc_gate(x, self.Wix, self.Wih,
self.bi, self.gate_activator)
self.i_list.append(ig)
# 輸出門
og = self.calc_gate(x, self.Wox, self.Woh,
self.bo, self.gate_activator)
self.o_list.append(og)
# 即時狀態
ct = self.calc_gate(x, self.Wcx, self.Wch,
self.bc, self.output_activator)
self.ct_list.append(ct)
# 單元狀態
c = fg * self.c_list[self.times - 1] + ig * ct
self.c_list.append(c)
# 輸出
h = og * self.output_activator.forward(c)
self.h_list.append(h)
def calc_gate(self, x, Wx, Wh, b, activator):
'''
計算門
'''
h = self.h_list[self.times - 1] # 上次的LSTM輸出
net = np.dot(Wh, h) + np.dot(Wx, x) + b
gate = activator.forward(net)
return gate從上面的程式碼我們可以看到,門的計算都是相同的演算法,而門和的計算僅僅是啟用函式不同。因此我們提出了calc_gate方法,這樣減少了很多重複程式碼。
反向傳播演算法的實現
backward方法實現了LSTM的反向傳播演算法。需要注意的是,與backword相關的內部狀態變數是在呼叫backward方法之後才初始化的。這種延遲初始化的一個好處是,如果LSTM只是用來推理,那麼就不需要初始化這些變數,節省了很多記憶體。
def backward(self, x, delta_h, activator):
'''
實現LSTM訓練演算法
'''
self.calc_delta(delta_h, activator)
self.calc_gradient(x)演算法主要分成兩個部分,一部分使計算誤差項:
def calc_delta(self, delta_h, activator):
# 初始化各個時刻的誤差項
self.delta_h_list = self.init_delta() # 輸出誤差項
self.delta_o_list = self.init_delta() # 輸出門誤差項
self.delta_i_list = self.init_delta() # 輸入門誤差項
self.delta_f_list = self.init_delta() # 遺忘門誤差項
self.delta_ct_list = self.init_delta() # 即時輸出誤差項
# 儲存從上一層傳遞下來的當前時刻的誤差項
self.delta_h_list[-1] = delta_h
# 迭代計算每個時刻的誤差項
for k in range(self.times, 0, -1):
self.calc_delta_k(k)
def init_delta(self):
'''
初始化誤差項
'''
delta_list = []
for i in range(self.times + 1):
delta_list.append(np.zeros(
(self.state_width, 1)))
return delta_list
def calc_delta_k(self, k):
'''
根據k時刻的delta_h,計算k時刻的delta_f、
delta_i、delta_o、delta_ct,以及k-1時刻的delta_h
'''
# 獲得k時刻前向計算的值
ig = self.i_list[k]
og = self.o_list[k]
fg = self.f_list[k]
ct = self.ct_list[k]
c = self.c_list[k]
c_prev = self.c_list[k-1]
tanh_c = self.output_activator.forward(c)
delta_k = self.delta_h_list[k]
# 根據式9計算delta_o
delta_o = (delta_k * tanh_c *
self.gate_activator.backward(og))
delta_f = (delta_k * og *
(1 - tanh_c * tanh_c) * c_prev *
self.gate_activator.backward(fg))
delta_i = (delta_k * og *
(1 - tanh_c * tanh_c) * ct *
self.gate_activator.backward(ig))
delta_ct = (delta_k * og *
(1 - tanh_c * tanh_c) * ig *
self.output_activator.backward(ct))
delta_h_prev = (
np.dot(delta_o.transpose(), self.Woh) +
np.dot(delta_i.transpose(), self.Wih) +
np.dot(delta_f.transpose(), self.Wfh) +
np.dot(delta_ct.transpose(), self.Wch)
).transpose()
# 儲存全部delta值
self.delta_h_list[k-1] = delta_h_prev
self.delta_f_list[k] = delta_f
self.delta_i_list[k] = delta_i
self.delta_o_list[k] = delta_o
self.delta_ct_list[k] = delta_ct另一部分是計算梯度:
def calc_gradient(self, x):
# 初始化遺忘門權重梯度矩陣和偏置項
self.Wfh_grad, self.Wfx_grad, self.bf_grad = (
self.init_weight_gradient_mat())
# 初始化輸入門權重梯度矩陣和偏置項
self.Wih_grad, self.Wix_grad, self.bi_grad = (
self.init_weight_gradient_mat())
# 初始化輸出門權重梯度矩陣和偏置項
self.Woh_grad, self.Wox_grad, self.bo_grad = (
self.init_weight_gradient_mat())
# 初始化單元狀態權重梯度矩陣和偏置項
self.Wch_grad, self.Wcx_grad, self.bc_grad = (
self.init_weight_gradient_mat())
# 計算對上一次輸出h的權重梯度
for t in range(self.times, 0, -1):
# 計算各個時刻的梯度
(Wfh_grad, bf_grad,
Wih_grad, bi_grad,
Woh_grad, bo_grad,
Wch_grad, bc_grad) = (
self.calc_gradient_t(t))
# 實際梯度是各時刻梯度之和
self.Wfh_grad += Wfh_grad
self.bf_grad += bf_grad
self.Wih_grad += Wih_grad
self.bi_grad += bi_grad
self.Woh_grad += Woh_grad
self.bo_grad += bo_grad
self.Wch_grad += Wch_grad
self.bc_grad += bc_grad
print '-----%d-----' % t
print Wfh_grad
print self.Wfh_grad
# 計算對本次輸入x的權重梯度
xt = x.transpose()
self.Wfx_grad = np.dot(self.delta_f_list[-1], xt)
self.Wix_grad = np.dot(self.delta_i_list[-1], xt)
self.Wox_grad = np.dot(self.delta_o_list[-1], xt)
self.Wcx_grad = np.dot(self.delta_ct_list[-1], xt)
def init_weight_gradient_mat(self):
'''
初始化權重矩陣
'''
Wh_grad = np.zeros((self.state_width,
self.state_width))
Wx_grad = np.zeros((self.state_width,
self.input_width))
b_grad = np.zeros((self.state_width, 1))
return Wh_grad, Wx_grad, b_grad
def calc_gradient_t(self, t):
'''
計算每個時刻t權重的梯度
'''
h_prev = self.h_list[t-1].transpose()
Wfh_grad = np.dot(self.delta_f_list[t], h_prev)
bf_grad = self.delta_f_list[t]
Wih_grad = np.dot(self.delta_i_list[t], h_prev)
bi_grad = self.delta_f_list[t]
Woh_grad = np.dot(self.delta_o_list[t], h_prev)
bo_grad = self.delta_f_list[t]
Wch_grad = np.dot(self.delta_ct_list[t], h_prev)
bc_grad = self.delta_ct_list[t]
return Wfh_grad, bf_grad, Wih_grad, bi_grad, \
Woh_grad, bo_grad, Wch_grad, bc_grad梯度下降演算法的實現
下面是用梯度下降演算法來更新權重:
def update(self):
'''
按照梯度下降,更新權重
'''
self.Wfh -= self.learning_rate * self.Whf_grad
self.Wfx -= self.learning_rate * self.Whx_grad
self.bf -= self.learning_rate * self.bf_grad
self.Wih -= self.learning_rate * self.Whi_grad
self.Wix -= self.learning_rate * self.Whi_grad
self.bi -= self.learning_rate * self.bi_grad
self.Woh -= self.learning_rate * self.Wof_grad
self.Wox -= self.learning_rate * self.Wox_grad
self.bo -= self.learning_rate * self.bo_grad
self.Wch -= self.learning_rate * self.Wcf_grad
self.Wcx -= self.learning_rate * self.Wcx_grad
self.bc -= self.learning_rate * self.bc_grad梯度檢查的實現
和RecurrentLayer一樣,為了支援梯度檢查,我們需要支援重置內部狀態:
def reset_state(self):
# 當前時刻初始化為t0
self.times = 0
# 各個時刻的單元狀態向量c
self.c_list = self.init_state_vec()
# 各個時刻的輸出向量h
self.h_list = self.init_state_vec()
# 各個時刻的遺忘門f
self.f_list = self.init_state_vec()
# 各個時刻的輸入門i
self.i_list = self.init_state_vec()
# 各個時刻的輸出門o
self.o_list = self.init_state_vec()
# 各個時刻的即時狀態c~
self.ct_list = self.init_state_vec()最後,是梯度檢查的程式碼:
def data_set():
x = [np.array([[1], [2], [3]]),
np.array([[2], [3], [4]])]
d = np.array([[1], [2]])
return x, d
def gradient_check():
'''
梯度檢查
'''
# 設計一個誤差函式,取所有節點輸出項之和
error_function = lambda o: o.sum()
lstm = LstmLayer(3, 2, 1e-3)
# 計算forward值
x, d = data_set()
lstm.forward(x[0])
lstm.forward(x[1])
# 求取sensitivity map
sensitivity_array = np.ones(lstm.h_list[-1].shape,
dtype=np.float64)
# 計算梯度
lstm.backward(x[1], sensitivity_array, IdentityActivator())
# 檢查梯度
epsilon = 10e-4
for i in range(lstm.Wfh.shape[0]):
for j in range(lstm.Wfh.shape[1]):
lstm.Wfh[i,j] += epsilon
lstm.reset_state()
lstm.forward(x[0])
lstm.forward(x[1])
err1 = error_function(lstm.h_list[-1])
lstm.Wfh[i,j] -= 2*epsilon
lstm.reset_state()
lstm.forward(x[0])
lstm.forward(x[1])
err2 = error_function(lstm.h_list[-1])
expect_grad = (err1 - err2) / (2 * epsilon)
lstm.Wfh[i,j] += epsilon
print 'weights(%d,%d): expected - actural %.4e - %.4e' % (
i, j, expect_grad, lstm.Wfh_grad[i,j])
return lstm我們只對做了檢查,讀者可以自行增加對其他梯度的檢查。下面是某次梯度檢查的結果:

GRU
前面我們講了一種普通的LSTM,事實上LSTM存在很多變體,許多論文中的LSTM都或多或少的不太一樣。在眾多的LSTM變體中,GRU (Gated Recurrent Unit)也許是最成功的一種。它對LSTM做了很多簡化,同時卻保持著和LSTM相同的效果。因此,GRU最近變得越來越流行。
GRU對LSTM做了兩個大改動:
-
將輸入門、遺忘門、輸出門變為兩個門:更新門(Update Gate)Zt和重置門(Reset Gate)rt。
-
將單元狀態與輸出合併為一個狀態:h。
GRU的前向計算公式為:
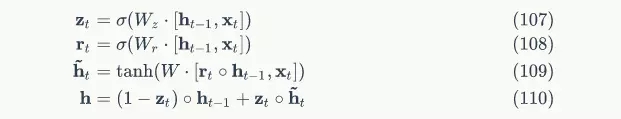
下圖是GRU的示意圖:
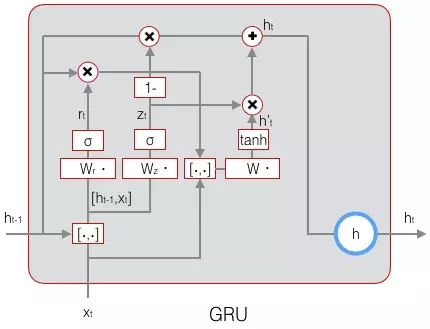
GRU的訓練演算法比LSTM簡單一些,留給讀者自行推導,本文就不再贅述了。
小結
至此,LSTM——也許是結構最複雜的一類神經網路——就講完了,相信拿下前幾篇文章的讀者們搞定這篇文章也不在話下吧!現在我們已經瞭解迴圈神經網路和它最流行的變體——LSTM,它們都可以用來處理序列。但是,有時候僅僅擁有處理序列的能力還不夠,還需要處理比序列更為複雜的結構(比如樹結構),這時候就需要用到另外一類網路:遞迴神經網路(Recursive Neural Network),巧合的是,它的縮寫也是RNN。在下一篇文章中,我們將介紹遞迴神經網路和它的訓練演算法。
原文:https://zybuluo.com/hanbingtao/note/581764
相關推薦
零基礎入門深度學習(6)
在上一篇文章《零基礎入門深度學習(4):迴圈神經網路》中,我們介紹了迴圈神經網路以及它的訓練演算法。我們也介紹了迴圈神經網路很難訓練的原因,這導致了它在實際應用中,很難處理長距離的依賴。在本文中,我們將介紹一種改進之後的迴圈神經網路:長短時記憶網路(Long Short
【轉載】《零基礎入門深度學習》系列文章(教程+程式碼)
轉自:https://blog.csdn.net/TS1130/article/details/53244576 無論即將到來的是大資料時代還是人工智慧時代,亦或是傳統行業使用人工智慧在雲上處理大資料的時代,作為一個有理想有追求的程式設計師,不懂深度學習(Deep Learning)這個超熱的技
零基礎入門深度學習(5)
原址 無論即將到來的是大資料時代還是人工智慧時代,亦或是傳統行業使用人工智慧在雲上處理大資料的時代,作為一個有理想有追求的程式設計師,不懂深度學習(Deep Learning)這個超熱的技術,會不會感覺馬上就out了?現在救命稻草來了,《零基礎入門深
零基礎入門深度學習(1)
深度學習是啥 在人工智慧領域,有一個方法叫機器學習。在機器學習這個方法裡,有一類演算法叫神經網路。神經網路如下圖所示: 上圖中每個圓圈都是一個神經元,每條線表示神經元之間的連線。我們可以看到,上面的神經元被分成了多層,層與層之間的神經元有連線,而層內之間的神經元沒有連線。
零基礎入門深度學習(2)
往期回顧 在上一篇文章中,我們已經學會了編寫一個簡單的感知器,並用它來實現一個線性分類器。你應該還記得用來訓練感知器的『感知器規則』。然而,我們並沒有關心這個規則是怎麼得到的。本文通過介紹另外一種『感知器』,也就是『線性單元』,來說明關於機器學習一些基本的概念,比如模型、
[轉]《零基礎入門深度學習》系列文章(教程+程式碼)
無論即將到來的是大資料時代還是人工智慧時代,亦或是傳統行業使用人工智慧在雲上處理大資料的時代,作為一個有理想有追求的程式設計師,不懂深度學習(Deep Learning)這個超熱的技術,會不會感覺馬上就out了?現在救命稻草來了,《零基礎入門深度學習》系列文章旨
零基礎入門深度學習(4)
往期回顧 在前面的文章中,我們介紹了全連線神經網路,以及它的訓練和使用。我們用它來識別了手寫數字,然而,這種結構的網路對於影象識別任務來說並不是很合適。本文將要介紹一種更適合影象、語音識別任務的神經網路結構——卷積神經網路(Convolutional Neu
21 天零基礎入門機器學習 , 高薪 Offer 就在眼前
今天,想真誠地講個故事,分享給大家一個來自《極簡機器學習入門》的學員天明同學的真實學習事例。 天明在 2013 年畢業,做過平行計算開發、嵌入式底層,目前在遊戲創業公司做伺服器開發,以下是他自從學習這門課之後的一些進展情況。 背景 我報名的是針對 AI 的入門課程,
零基礎使用深度學習進行目標檢測
實驗目的 下面這張影象存在9處瑕疵劃痕(使用微軟畫圖工具亂畫的),就是要檢測的目標。經過深度學習的訓練,可以預測新影象上是否有瑕疵和這些瑕疵的位置(以下這張圖是未參加訓練的測試圖)。 實驗效果 經過深度學習訓練後得出一個模型,利用該模型對測試圖片進行預測,其預測效果如下圖
從零基礎成為深度學習高手——Ⅱ
今天繼續昨天的知識,繼續學習新的一個階段知識:深度學習基礎知識 接下來我們瞭解一下基礎知識,我
html5該怎麽樣學習?零基礎入門HTML5學習路線
html5開發 ejs nodejs基礎 程序設計 管理 高端 修改 公司 項目開發 縱觀近幾年HTML5的發展可以看出,HTML5開發持續上漲,騰訊、微軟、谷歌等國際互聯網企業都將HTML5的研發與使用放在了重要的地位。目前全球有超過十億臺手機瀏覽器支持HTML5,而微信
《零基礎入門學習Python》第058講:論一隻爬蟲的自我修養6:正則表示式2
上一節課我們通過一個例子(匹配 ip 地址)讓大家初步瞭解到正則表示式的魔力,也讓大家充分了解到學習正則表示式是一個相對比較困難的事情。所以這一節課我們將繼續學習 正則表示式的語法。 我們依稀還記得在Python中,正則表示式是以字串的形式來描述的,正則表示式的強大之處在於特殊符號的應用,我
《零基礎入門學習Python》第095講:Pygame:飛機大戰6
今天繼續飛機大戰的開發,遊戲每30秒就隨機下放一個補給包,可能是超級子彈或者全屏炸彈。 補給包有自己的圖片(如下圖),也有自己的執行軌跡(由上而下) 因此,我們可以單獨寫一個模組來實現:命名為 supply #supply.py import pygame from random i
深度學習零基礎入門零
畢業設計是和深度學習相關,之前零零碎碎的學習了一些相關知識,這裡開個系列文章總結一些,以免又看了忘,再看又不方便。 深度學習目前可以說是非常火了,而深度學習是機器學習的一個分支,機器學習也只是人工智慧的一個分支。 我是跟著李巨集毅教授的上課視訊一起學,這是地址 h
零基礎入門學習python[小甲魚]--就這麽愉快地開始吧01
inf 基礎 tro str 利用 build ice size 輸入 1. 從IDIE啟動python IDLE是一個python shell,shell的意思就是“外殼”,從基本上說,就是一個通過輸入本與程序交互的途徑。像windows的cmd的窗口,像
Python零基礎入門(6)-------數值類型
math 工具 int() ber 情況 info 獲得 浮點型 log int、float 類型 Python的 int 、float 類型相對於其他語言的沒有明確的範圍限制,Python 的 int 、float 類型能存儲多大的數值是由硬件決定 十進制可以直接寫
2018年《selenium+python3.6課程》3月31號開學- 零基礎入門包教會
3.3 strong python3.6 select blog ive 基礎入門 drive 數據類型 《selenium+python3.6零基礎入門到提升班》開課時間:2018.3.31上課方式:QQ群(上課小群)在線視頻,課後錄視頻上課時間:見課表(周六和周日晚上8
零基礎入門學習Web開發(HTML5&CSS3)007<noscript><script>
驗證 文件 入門 指向 腳本文件 mime syn 使用 javascrip 0.<script> HTML <script> 標簽 定義和用法 <script> 標簽用於定義客戶端腳本,比如 JavaScript。 script
《零基礎入門學習Python》(11)--列表:一個打了激素的陣列(二)
前言 上節課我們介紹一個打了激素的陣列,叫做列表。列表我們比作一個大倉庫,你所能夠具現化的東西,都可以往裡面扔,它包羅永珍。另外還介紹了三個往列表新增元素的方法,分別是: append(),extend(),insert() append()和extend()這兩個方法都只有1個引數:
