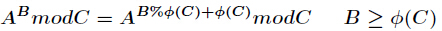2016多校訓練一 PowMod,hdu5728(尤拉函式+指數迴圈節)
k=∑mi=1φ(i∗n)mod1000000007
n is a square-free number.
φ is the Euler's totient function.
find:
ans=kkkk...kmodp
There are infinite number of k
Input Multiple test cases(test cases ≤100), one line per case.
Each line contains three integers, n,m and p.
1≤n,m,p≤107
Output For each case, output a single line with one integer, ans.
Sample Input 1 2 6 1 100 9
Sample Output 4 7
題意:只要是那個k是無限個
題解:首先是算k:先了解兩條性質,尤拉函式是積性函式;
(1)積性函式性質:F(m1*m2)=F(m1)*F(m2),當且近當gcd(m1,m2)=1時成立;
(2)
有了這個再來算k,題目的n是很特殊的,它的每個素因子的冪次都是1:
那麼假設素數p是n的一個素因子,顯然gcd(p,n/p)=1;關鍵是i,如果i中沒有素因子p,那麼就直接用積性性質。如果i%p==0,必然可以寫成i=k*p;即倍數關係,否則i%p!=0;
所以分成兩部分求:

到這裡前兩和式是可以合併的,考慮和式的上下限,含義不同,第二項的i表示的p的倍數i*p才是第一項i的含義,相當於第二項剛好把第一項補齊了,那麼從1到m沒有遺漏,而且第二項的i用第一項替換后里面也是n/p;最終
這是個二元遞迴式:n/p和m/p看成整體,那麼設原先求的為f(n,m),所以f(n,m)=(p的尤拉值)*f(n/p,m)+f(n,m/p);
每次列舉一個就夠了,n每次要除以p,最多就是把它的每個素因子除完。
第二部分k的超級冪:用尤拉的定理:指數迴圈節
每次往冪次上一層模就取一次尤拉值,只有1的尤拉值等一自己,其他數的尤拉值都是小於自己的,所以模會不斷變小至1,顯然對1取模結果就是0,所以無限就變得有限了
#include<cstdio> #include<cstring> #include<string> #include<iostream> #include<sstream> #include<algorithm> #include<utility> #include<vector> #include<set> #include<map> #include<queue> #include<cmath> #include<iterator> #include<stack> using namespace std; const int INF=1e9+7; const double eps=1e-7; const int N=1e7+5; const int M=1000000007; typedef long long ll; int pri[N],phi[N]; bool vis[N]; int tot; ll sum[N]; void init() { int n=N; tot=0; memset(vis,false,sizeof vis); phi[1]=1; for(int i=2;i<n;i++) { if(!vis[i]) { pri[tot++]=i; phi[i]=i-1; } for(int j=0;j<tot && i*pri[j]<n;j++) { vis[i*pri[j]]=true; if(i%pri[j]==0) { phi[i*pri[j]]=phi[i]*pri[j]; break; } else phi[i*pri[j]]=phi[i]*(pri[j]-1); } } sum[0]=0; for(int i=1;i<N;i++) sum[i]=(sum[i-1]+phi[i])%M; } ll Pow(ll a,ll n,ll mod) { ll ans=1; while(n) { if(n&1) { ans=ans*a%mod; // if(ans>=mod)ans=ans%mod; } a=a*a%mod; // if(a>=mod) a=a%mod; n>>=1; } if(ans==0) ans+=mod; return ans; } ll solve(ll k,ll mod) { if(mod==1) return mod; ll tmp=phi[mod]; ll up=solve(k,tmp); ll ans=Pow(k,up,mod); return ans; } int rear; int a[15]; void resolve(ll n) { for(int i=0;i<tot;i++) { if(!vis[n]) {a[rear++]=n;break;} if(n%pri[i]==0) { a[rear++]=pri[i]; n/=pri[i]; } } } ll f(int pos,ll n,ll m) { //pos即每個素數,一次一個就行了 if(n==1) return sum[m];//n為1結果就是尤拉值的字首和 if(m==0)return 0; return ((a[pos]-1)*f(pos-1,n/a[pos],m)%M+f(pos,n,m/a[pos]))%M; } int main() { init();//打表 ll n,m,p; while(~scanf("%I64d%I64d%I64d",&n,&m,&p)) { rear=0; resolve(n);//素因子分解 ll k=f(rear-1,n,m);//算k ll ans=solve(k,p); printf("%I64d\n",ans%p); } return 0; }
相關推薦
2016多校訓練一 PowMod,hdu5728(尤拉函式+指數迴圈節)
Declare:k=∑mi=1φ(i∗n)mod1000000007n is a square-free number.φ is the Euler's totient function. find:ans=kkkk...kmodp There are infini
牛客多校第四場A ternary string ----推公式和指數迴圈節
Ternary String 時間限制:C/C++ 4秒,其他語言8秒 空間限制:C/C++ 131072K,其他語言262144K 64bit IO Format: %lld 題目描述 A ternary string is a sequenc
2016多校訓練#5 1012 HDU 5792 樹狀陣列 程式碼詳解
World is Exploding Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others) Total Submission(s
2016多校訓練Contest10: 1002 Hard problem hdu5858
Problem Description cjj is fun with math problem. One day he found a Olympic Mathematics problem for primary school students. It is to
2016多校訓練#1 1002 組合博弈
對於一開始接觸博弈論的同學來說,這道題的思路略難,但是如果想到了把1*20的棋盤想象成一個20位的二進位制數,然後通過sg函式預處理得到每一個二進位制數相應的sg'值,最後直接用每一行的sg值相亦或即可。注意mex陣列,也就是vis陣列可以開得大
hdu5821(2016多校第8場,暴力)
ZZX has a sequence of boxes numbered 1,2,...,n. Each box can contain at most one ball. You are given the initial configuration of the balls. For 1≤i≤n, i
牛客網多校訓練第一場 I - Substring(後綴數組 + 重復處理)
.com get 處理 man string target span roman targe 鏈接: https://www.nowcoder.com/acm/contest/139/I 題意: 牛客網多校訓練第一場 I - Substring(後綴數組 + 重復處理
HDU 5728 PowMod(數論,尤拉函式的各種性質)
[題意] k=∑i=1mϕ(i∗n)%1000000007 其中n為無平方因子的數,求 ans=kkkk...k%p [分析] n無平方因子說明n可以表示為n=p1∗p2∗...∗pl
[HDU 5728] PowMod (尤拉函式的積性+尤拉公式降冪+尤拉篩)
HDU - 5728 求 K=∑i=1mϕ(i∗n)mod1000000007 其中 n是 square-free number 求 ans=KKKK..modp 先求 K 由於 ϕ(n)是積性函式,所以對於 n的每個素因子可以提出
51nod 1040 求1-n這n個數,同n的最大公約數的和(尤拉函式)
題目:給出一個n,求1-n這n個數,同n的最大公約數的和。比如:n = 6 1,2,3,4,5,6 同6的最大公約數分別為1,2,3,2,1,6,加在一起 = 15 思路:一個數與n的最大公約數肯定是n的因子中的一個,所以只需要列舉n的每一個因子x,然
【數論】線性篩素數,線性篩尤拉函式,求前N個數的約數個數
先來最基本的線性篩素數,以後的演算法其實都是基於這個最基本的演算法: #include<stdio.h> #include<string.h> #define M 10000000 int prime[M/3]; bool flag[M]; void
HDU 5820 Lights (2016多校7L,主席樹)
題意 給定n個平面上的點,座標範圍為[1, 50000]。如果對於任意兩個點,都可以通過直走(中途經過其他點)走到。 那麼輸出YES,否則輸出NO。 首先排序,去重。 我們要找的點對是隻能斜對角走到的點。 那麼找到這個點正左邊的離他最近的點和正上方最近的點。查詢以這三
HDU5823(2016多校第八場)——color II (狀壓dp,獨立集)
First line contains an integer t. Then t testcases follow. In each testcase: First line contains an integer n. Next n lines each contains a string consis
HDU 5732 2016多校Contest 1 Subway【找樹的重心,判斷樹的同構】
題目大意: 給定一棵樹,這兩棵樹肯定是同構的。 問你,第一棵樹的每個節點,可以對應第二個樹的那個節點。 顯然對應方法不唯一,SPJ來檢測結果正確。 方法: 首先找樹的重心, 樹的重心最多2個。 一個重心的情況很多,兩個重心的情況如圖: 有人說這個圖太對稱了……
HDU 4920(杭電多校訓練#5 1010 題) Matrix multiplication(不知道該掛個什麽帽子。。。)
預處理 ica ref 循環 ring sca esp 題解 code 題目地址:HDU 4920 對這個題簡直無語到極點。。。竟然O(n^3)的復雜度能過。。。。方法有三。。 1:進行輸入優化和輸出優化。。(前提是你的輸入優化不能太搓。。。) 2:利用緩存優化。。詳情
【鏈表】2017多校訓練3 HDU 6058 Kanade's sum
iostream ++ 多校 open pos cnblogs names mat play acm.hdu.edu.cn/showproblem.php?pid=6058 【題意】 給定一個排列,計算 【思路】 計算排列A中每個數的貢獻,即對於每個ai,計算有
2016多校第4場 HDU 6076 Security Check DP,思維
pro begin sizeof || i++ 預處理 通過 第一個 ans 題目鏈接:http://acm.hdu.edu.cn/showproblem.php?pid=6076 題意:現要檢查兩條隊伍,有兩種方式,一種是從兩條隊伍中任選一條檢查一個人,第二種是在每條隊伍
【組合數+Lucas定理】2017多校訓練七 HDU 6129 Just do it
clu sca def opened == cnblogs long 合數 color http://acm.hdu.edu.cn/showproblem.php?pid=6129 【題意】 對於一個長度為n的序列a,我們可以計算b[i]=a1^a2^......^ai,
【雙向bfs】2017多校訓練十 HDU 6171 Admiral
isp hide splay 編號 sig push pac ans logs 【題意】 現在給出一個三角矩陣,如果0編號的在點(x,y)的話,可以和(x+1,y),(x-1,y),(x+1,y+1),(x-1,y-1)這些點進行交換。 我們每一次只能對0點和其他點進行交
牛客網多校訓練 道路問題
一個 question 有道 void lib 以及 -h 測試 iostream 題目描述 隨著如今社會的不斷變化,交通問題也變得越來越重要,所以市長決定建設一些公路來方便各個城市之間的貿易和交易。雖然市長的想法很好,但是他也遇到了一般人也經常頭疼的問題,那就是手頭