資料結構-二叉樹和二叉查詢樹
先按樹-二叉樹-二叉查詢樹的順序解釋會比較清楚。
一,樹
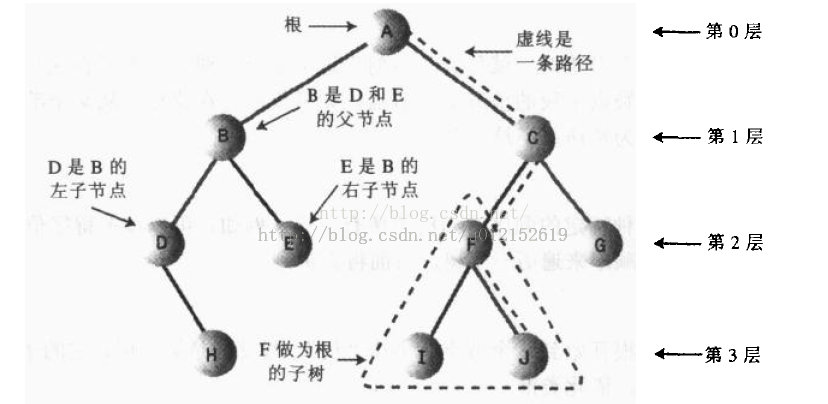
樹(Tree)是n(n≥0)個結點的有限集。在任意一棵非空樹中:
(1)有且僅有一個特定的被稱為根(Root)的結點;
(2)當n>1時,其餘結點可分為m(m>0)個互不相交的有限集T1,T2,…,Tm,其中每一個集合本身又是一棵樹,並且稱為根的子樹(SubTree)。
結點的度(Degree):結點擁有的子樹數稱為結點的度(Degree)。度為0的結點稱為葉子(Leaf)或終端結點。度不為0的結點稱為非終端結點或分支結點。樹的度:是樹內各結點的度的最大值。
孩子和雙親:結點的子樹的根稱為該結點的孩子(Child),相應地,該結點稱為孩子的雙親(Parent)。
結點的層次(Level):
如果將樹中結點的各子樹看成從左至右是有次序的(即不能互換),則稱該樹為有序樹,否則稱為無序樹。
二,二叉樹
二叉樹(Binary Tree)的特點是每個結點至多具有兩棵子樹(即在二叉樹中不存在度大於2的結點),並且子樹之間有左右之分。
二叉樹的性質:
(1)、在二叉樹的第i層上至多有2i-1個結點(i≥1)。
(2)、深度為k的二叉樹至多有2k-1個結點(k≥1)。
(3)、對任何一棵二叉樹,如果其終端結點數為n0,度為2的結點數為n2,則n0=n2+1。
三,二叉查詢樹(左<中<右)
我們從一種特殊的、使用很廣泛的二叉樹入手:二叉查詢樹。
二叉查詢樹的性質:
(1)、若它的左子樹不為空,則左子樹上所有結點的值均小於它的根結點的值;
(2)、若它的右子樹不為空,則右子樹上所有結點的值均大於它的根結點的值;
(3)、它的左、右子樹也分別為二叉查詢樹。
用一句話概括,二叉查詢樹的特點是,一個節點的左子節點的關鍵字值小於這個節點,右子節點的關鍵字值大於或等於這個父節點。
二叉查詢樹的基本操作是查詢,插入,刪除,遍歷,下面一一介紹:
1,查詢(search)
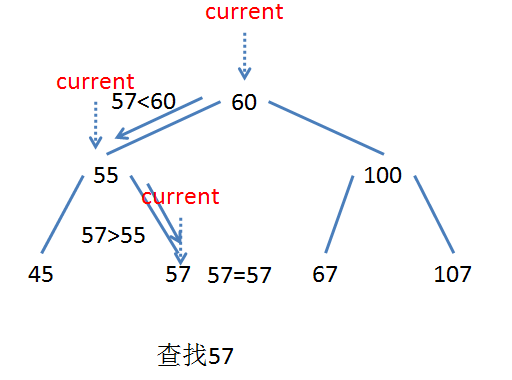
我們已經知道,二叉搜尋樹的特點是左子節點小於父節點,右子節點大於或等於父節點。查詢某個節點時,先從根節點入手,如果該元素值小於根節點,則轉向左子節點,否則轉向右子節點,以此類推,直到找到該節點,或者到最後一個葉子節點依然沒有找到,則證明樹中沒有該節點
程式碼是:
/** 查詢元素,返回true */
public boolean search(E e) {
TreeNode<E> current = root; // 從根元素開始
while (current != null) {
if (e.compareTo(current.element) < 0) {//如果比當前元素值小,就指向當前元素的左子樹
current = current.left;
}
else if (e.compareTo(current.element) > 0) {//如果比當前元素值大,就指向當前元素的右子樹
current = current.right;
}
else // element等於 current.element
return true; //發現元素,返回true
}
return false;
}2,插入(insert)
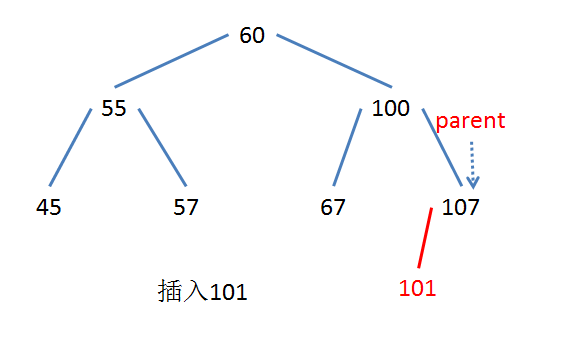
插入一個新節點首先要確定插入的位置,關鍵思路是確定新節點父節點所在的位置。
程式碼:
/** 插入元素,成功返回true */
public boolean insert(E e) {
if (root == null)
root = createNewNode(e); // 如果是樹空則創造一個跟節點
else {
// 標記當前父節點位置
TreeNode<E> parent = null;
TreeNode<E> current = root;
while (current != null)
if (e.compareTo(current.element) < 0) {
parent = current;
current = current.left;
}
else if (e.compareTo(current.element) > 0) {
parent = current;
current = current.right;
}
else
return false; // 有重複節點,不能被插入
// 建立一個新節點掛在父節點下
if (e.compareTo(parent.element) < 0)
parent.left = createNewNode(e);
else
parent.right = createNewNode(e);
}
size++;
return true; // 插入成功
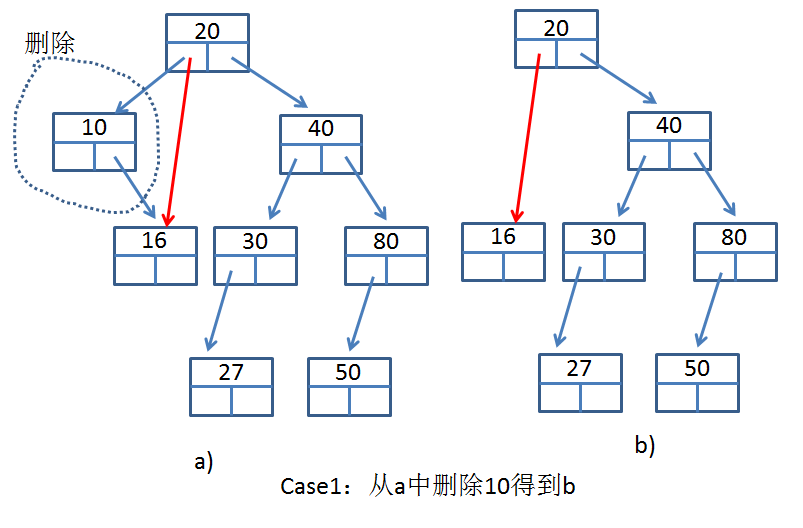
}刪除BST中的一個節點是最麻煩的操作,總結一下大概下面兩種方法:
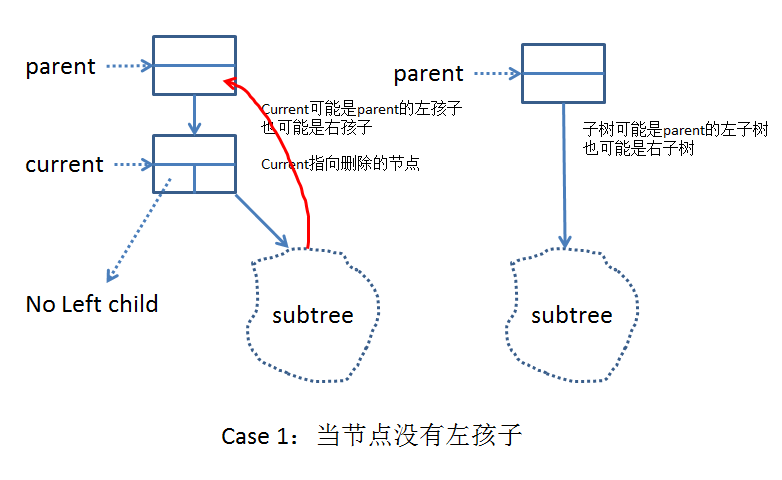
Case 1:刪除點沒有左孩子,這是隻需要將該節點的父節點和當前節點的有孩子相連即可
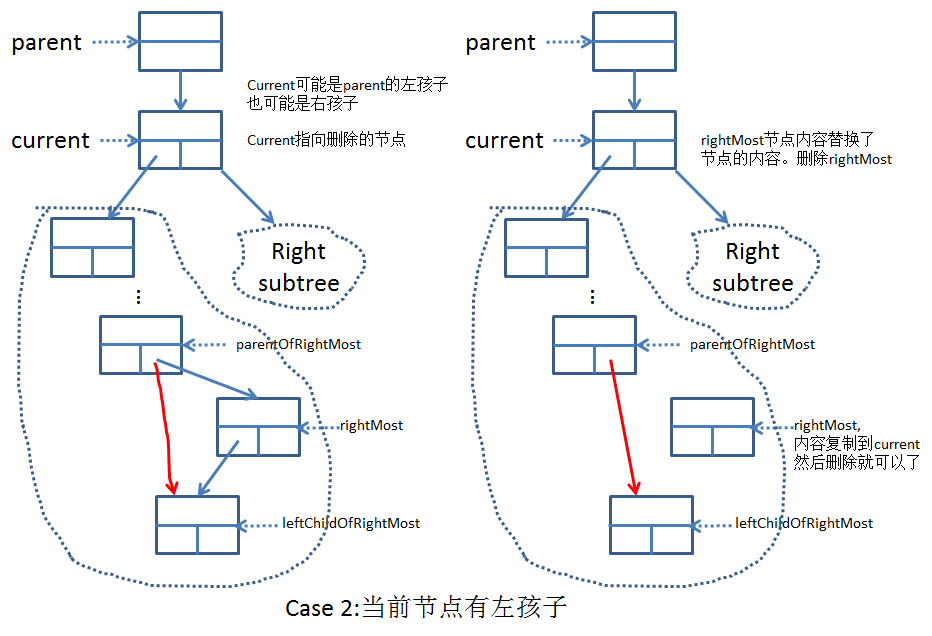
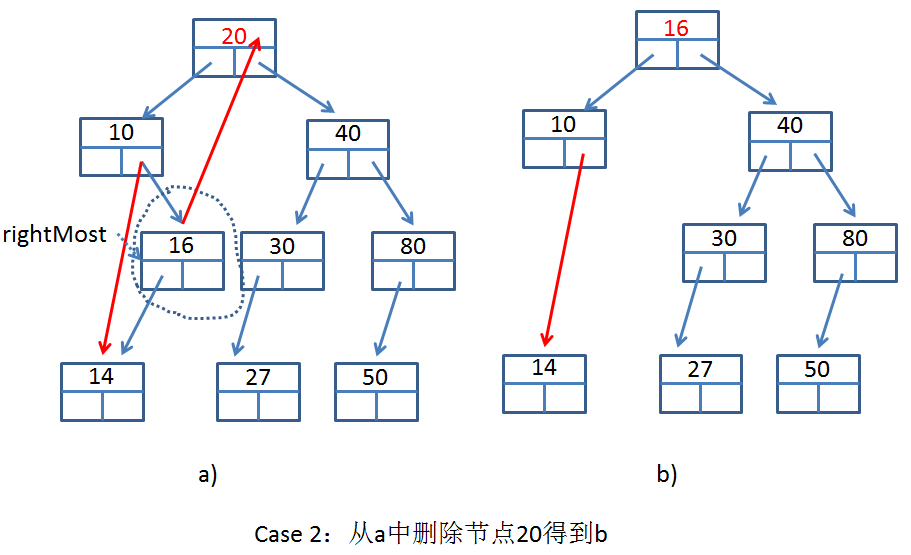
Case2:刪除點有左孩子.這種情況下先找到當前節點的左子樹的最右節點,因為一個節點的左子樹的最右節點也比右子樹的最左節點小,把最右節點複製給刪除點,然後刪除最右節點
程式碼:
/** 刪除節點,刪除成功返回true,不在樹中返回false*/
public boolean delete(E e) {
// 標記被刪除的節點和該節點的父節點位置
TreeNode<E> parent = null;
TreeNode<E> current = root;
while (current != null) {
if (e.compareTo(current.element) < 0) {
parent = current;
current = current.left;
}
else if (e.compareTo(current.element) > 0) {
parent = current;
current = current.right;
}
else
break; // 元素在這個樹中
}
if (current == null)
return false; // 元素不在樹中
if (current.left == null) { // 第一種情況:元素沒有左子樹,把當前節點的右子樹直接掛在其父節點的右子樹上
// 把當前節點的右子樹直接掛在其父節點的右子樹上
if (parent == null) {
root = current.right;
}
else {
if (e.compareTo(parent.element) < 0)
parent.left = current.right;
else
parent.right = current.right;
}
}
else { // 第二種情況:元素有左子樹,先找到當前節點的左子樹的最右節點
//標記當前節點的左子樹的父節點和最右節點
TreeNode<E> parentOfRightMost = current;
TreeNode<E> rightMost = current.left;
//一直向右,找到最右端的節點,因為一個節點的左子樹的最右節點也比右子樹的最左節點小
while (rightMost.right != null) {
parentOfRightMost = rightMost;
rightMost = rightMost.right; // 一直向右
}
/*
* 以上程式碼的目的是要找到刪除節點的左子樹最右節點 ,因為一個節點的左子樹的最右節點也比右子樹的最左節點小*/
// 找到最右節點後,放到當前要刪除的位置
current.element = rightMost.element;
// 消除最右節點
if (parentOfRightMost.right == rightMost)
parentOfRightMost.right = rightMost.left;//把最右節點的左子樹掛在其父節點的右子樹上
else
// 具體情況: parentOfRightMost == current
parentOfRightMost.left = rightMost.left;
}
size--;
return true; // 刪除成功
}
下面介紹一下二叉樹的構成:
Tree.java
package com.hust.cn;
public interface Tree<E extends Comparable<E>> {
//查詢元素
public boolean search(E e);
//插入元素
public boolean insert(E e);
//刪除元素
public boolean delete(E e);
//中序遍歷
public void inorder();
//後序遍歷
public void postorder();
//前序遍歷
public void preorder();
//返回大小
public int getSize();
//判空
public boolean isEmpty();
//返回樹的迭代器
public java.util.Iterator iterator();
}
package com.hust.cn;
public abstract class AbstractTree<E extends Comparable<E>>
implements Tree<E> {
//中序遍歷
public void inorder() {
}
//後序遍歷
public void postorder() {
}
//前序遍歷
public void preorder() {
}
//判空
public boolean isEmpty() {
return getSize() == 0;
}
//返回樹的迭代器
public java.util.Iterator iterator() {
return null;
}
}
package com.hust.cn;
public class BinaryTree<E extends Comparable<E>>
extends AbstractTree<E> {
protected TreeNode<E> root;//節點類,是內部類
protected int size = 0;
/** 建構函式 */
public BinaryTree() {
}
/** 物件陣列建立一個二叉查詢樹 */
public BinaryTree(E[] objects) {
for (int i = 0; i < objects.length; i++)
insert(objects[i]);
}
/** 查詢元素,返回true */
public boolean search(E e) {
TreeNode<E> current = root; // 從根元素開始
while (current != null) {
if (e.compareTo(current.element) < 0) {//如果比當前元素值小,就指向當前元素的左子樹
current = current.left;
}
else if (e.compareTo(current.element) > 0) {//如果比當前元素值大,就指向當前元素的右子樹
current = current.right;
}
else // element等於 current.element
return true; //發現元素,返回true
}
return false;
}
/** 插入元素,成功返回true */
public boolean insert(E e) {
if (root == null)
root = createNewNode(e); // 如果是樹空則創造一個跟節點
else {
// 標記當前父節點位置
TreeNode<E> parent = null;
TreeNode<E> current = root;
while (current != null)
if (e.compareTo(current.element) < 0) {
parent = current;
current = current.left;
}
else if (e.compareTo(current.element) > 0) {
parent = current;
current = current.right;
}
else
return false; // 有重複節點,不能被插入
// 建立一個新節點掛在父節點下
if (e.compareTo(parent.element) < 0)
parent.left = createNewNode(e);
else
parent.right = createNewNode(e);
}
size++;
return true; // 插入成功
}
/*建立一個新節點*/
protected TreeNode<E> createNewNode(E e) {
return new TreeNode<E>(e);
}
/** 中序遍歷*/
public void inorder() {
inorder(root);
}
/** 從根節點中序遍歷 ,遞迴方法*/
protected void inorder(TreeNode<E> root) {
if (root == null) return;
inorder(root.left);
System.out.print(root.element + " ");
inorder(root.right);
}
/**後序遍歷 */
public void postorder() {
postorder(root);
}
/**從根節點後序遍歷,遞迴方法 */
protected void postorder(TreeNode<E> root) {
if (root == null) return;
postorder(root.left);
postorder(root.right);
System.out.print(root.element + " ");
}
/**前序遍歷 */
public void preorder() {
preorder(root);
}
/** 從根節點前序遍歷,遞迴方法 */
protected void preorder(TreeNode<E> root) {
if (root == null) return;
System.out.print(root.element + " ");
preorder(root.left);
preorder(root.right);
}
/** 返回樹的大小 */
public int getSize() {
return size;
}
/** 返回根節點 */
public TreeNode getRoot() {
return root;
}
/** 返回從根節點到一個具體元素的路徑 */
public java.util.ArrayList<TreeNode<E>> path(E e) {
java.util.ArrayList<TreeNode<E>> list =
new java.util.ArrayList<TreeNode<E>>();//用陣列存放路徑上的元素
TreeNode<E> current = root; // 從根節點開始
while (current != null) {
list.add(current); // 添加當前元素到數組裡
if (e.compareTo(current.element) < 0) {
current = current.left;
}
else if (e.compareTo(current.element) > 0) {
current = current.right;
}
else
break;
}
return list; // 返回節點陣列
}
/** 刪除節點,刪除成功返回true,不在樹中返回false*/
public boolean delete(E e) {
// 標記被刪除的節點和該節點的父節點位置
TreeNode<E> parent = null;
TreeNode<E> current = root;
while (current != null) {
if (e.compareTo(current.element) < 0) {
parent = current;
current = current.left;
}
else if (e.compareTo(current.element) > 0) {
parent = current;
current = current.right;
}
else
break; // 元素在這個樹中
}
if (current == null)
return false; // 元素不在樹中
if (current.left == null) { // 第一種情況:元素沒有左子樹,把當前節點的右子樹直接掛在其父節點的右子樹上
// 把當前節點的右子樹直接掛在其父節點的右子樹上
if (parent == null) {
root = current.right;
}
else {
if (e.compareTo(parent.element) < 0)
parent.left = current.right;
else
parent.right = current.right;
}
}
else { // 第二種情況:元素有左子樹,先找到當前節點的左子樹的最右節點
//標記當前節點的左子樹的父節點和最右節點
TreeNode<E> parentOfRightMost = current;
TreeNode<E> rightMost = current.left;
//一直向右,找到最右端的節點,因為一個節點的左子樹的最右節點也比右子樹的最左節點小
while (rightMost.right != null) {
parentOfRightMost = rightMost;
rightMost = rightMost.right; // 一直向右
}
/*
* 以上程式碼的目的是要找到刪除節點的左子樹最右節點 ,因為一個節點的左子樹的最右節點也比右子樹的最左節點小*/
// 找到最右節點後,放到當前要刪除的位置
current.element = rightMost.element;
// 消除最右節點
if (parentOfRightMost.right == rightMost)
parentOfRightMost.right = rightMost.left;//把最右節點的左子樹掛在其父節點的右子樹上
else
// 具體情況: parentOfRightMost == current
parentOfRightMost.left = rightMost.left;
}
size--;
return true; // 刪除成功
}
/** 獲得中序迭代器 */
public java.util.Iterator iterator() {
return inorderIterator();
}
/** 建立一個迭代器類*/
public java.util.Iterator inorderIterator() {
return new InorderIterator();
}
// 中序迭代器類,內部類
class InorderIterator implements java.util.Iterator {
// 儲存元素的陣列
private java.util.ArrayList<E> list =
new java.util.ArrayList<E>();
private int current = 0; //陣列中當前元素的位置
public InorderIterator() {
inorder(); // 中序遍歷二叉樹
}
/** 從根部中序遍歷*/
private void inorder() {
inorder(root);
}
/** 中序遍歷子樹 */
private void inorder(TreeNode<E> root) {
if (root == null)return;
inorder(root.left);
list.add(root.element);
inorder(root.right);
}
/** 遍歷下一個元素*/
public boolean hasNext() {
if (current < list.size())
return true;
return false;
}
/** 獲得當前元素,並把指標指向另一個元素 */
public Object next() {
return list.get(current++);
}
/** 移出當前元素 */
public void remove() {
delete(list.get(current)); //刪除當前元素
list.clear(); //清理陣列
inorder(); //重新中序遍歷陣列
}
}
/** 清楚樹的所有元素 */
public void clear() {
root = null;
size = 0;
}
/** 內部類,樹的節點類 */
public static class TreeNode<E extends Comparable<E>> {
E element;
TreeNode<E> left;
TreeNode<E> right;
public TreeNode(E e) {
element = e;
}
}
}
package com.hust.cn;
public class TestBinaryTree {
public static void main(String[] args) {
// 建立一個二叉查詢樹
BinaryTree<String> tree = new BinaryTree<String>();
tree.insert("George");
tree.insert("Michael");
tree.insert("Tom");
tree.insert("Adam");
tree.insert("Jones");
tree.insert("Peter");
tree.insert("Daniel");
// 遍歷樹
System.out.println("Inorder (sorted): ");
tree.inorder();
System.out.println("\nPostorder: ");
tree.postorder();
System.out.println("\nPreorder: ");
tree.preorder();
System.out.println("\nThe number of nodes is " + tree.getSize());
// 查詢一個元素
System.out.println("\nIs Peter in the tree? " +
tree.search("Peter"));
// 從root到peter的一條路徑
System.out.println("\nA path from the root to Peter is: ");
java.util.ArrayList<BinaryTree.TreeNode<String>> path
= tree.path("Peter");
for (int i = 0; path != null && i < path.size(); i++)
System.out.print(path.get(i).element + " ");
//利用陣列構建一個二叉查詢樹,並中序遍歷
Integer[] numbers = {2, 4, 3, 1, 8, 5, 6, 7};
BinaryTree<Integer> intTree = new BinaryTree<Integer>(numbers);
System.out.println("\nInorder (sorted): ");
intTree.inorder();
}
}
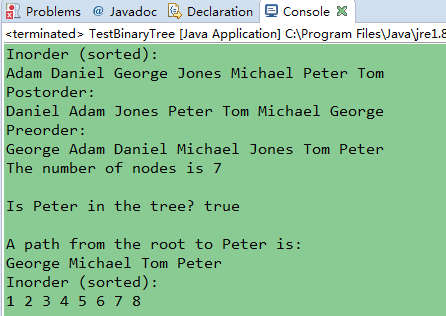
測試結果:
相關推薦
資料結構學習筆記-森林和二叉樹的轉化、最優二叉樹
int min(HuffmanTree &HT,int i) { int k = MAX; int j,flag = 0; for(j=1;j<=i;++j) { if(HT[j].weights2) { change = s1; s1 = s2; s2 = chang
資料結構作業10—陣列和廣義表以及樹的基本概念(選擇題)
2-1已知廣義表L=((x,y,z),a,(u,t,w)),從L表中取出原子項t的運算是()。 (2分) A.head(tail(head(tail(tail(L))))) B.head(tail(head(tail(L)))) C.tail(head(head
Java資料結構(十五)—— 多路查詢樹
多路查詢樹 二叉樹和B樹 二叉樹的問題分析 二叉樹操作效率高 二叉樹需要載入到記憶體,若二叉樹的節點多存在如下問題: 問題1:構建二叉樹時,需多次進行I/O操作,對與速度有影響 問題2:節點海量造成二叉樹的高度很大,會降低操作速度 多叉樹 在二叉樹中,每個節點有資料項,最多有兩個子節
資料結構——第三章樹和二叉樹:02二叉樹
1.二叉樹的儲存結構: (1)二叉樹的順序儲存表示: #define MAX_TREE_SIZE 100 //二叉樹的最大結點數 typedef TElemType SqBiTree[MAX_TREE_SIZE]; SqBiTree bt; (2)二叉樹的鏈式儲存表示: ①二叉連結
資料結構——第三章樹和二叉樹:03樹和森林
1.樹的三種儲存結構: (1)雙親表示法: #define MAX_TREE_SIZE 100 結點結構: typedef struct PTNode { Elem data; int parent; //雙親位置域 } PTNode; (2)孩子雙親連結串列表示法: &nbs
再談資料結構(二)數和二叉樹
1 - 引言 關於樹和二叉樹,我們需要達到的能力有: 熟悉樹和二叉樹的有關概念 熟悉二叉樹的性質 熟練掌握遍歷二叉樹的遞迴演算法,並靈活運用 遞迴遍歷二叉樹及其應用 本文著重在樹和二叉樹實際應用與程式碼實現基本操作,對概念就不再贅述 2 - 二
資料結構--樹和二叉樹03
8.平衡二叉樹 平衡二叉樹的定義:它或者是一棵空樹,或者樹的任意一結點的左右子鼠深度只差不會超過1,切記不可光比較根結點就進行斷定 平衡二叉樹提出的原因:如下圖傳入一個值,對該樹進行查詢比較,通過比較次數可知,平衡二叉樹結構更優 衡量一個排序二叉樹是否合格的指標 平衡二叉
資料結構--樹和二叉樹02
6.查詢樹(二叉排序樹)的基本定義 查詢二叉樹,又稱二叉排序樹。一棵查詢二叉樹,或為空樹,活滿足以下遞迴條件: 1.查詢樹的左右子樹各是一棵查詢樹 2.若查詢樹的左子樹非空,則左子樹上的各個結點值均小於根結點的值 3.若查詢樹的右子樹非空,則右子樹上的各個結點的值均大於根結點的值
資料結構--樹和二叉樹01
1.樹的基本概念: 樹的度:所有結點的度當中,度數最大的。 葉子結點:度為0的結點 分支結點:除了葉子節點以外,都是分支結點。 內部結點:除了葉子節點,和根節點以外所有的結點。 總結點為 N,總度數為K ,則 N = K +1
資料結構-王道-樹和二叉樹
樹和二叉樹 樹:是\(N(N\geq0)\)個結點的有限集合,\(N=0\)時,稱為空樹,這是一種特殊情況。在任意一棵非空樹中應滿足: 有且僅有一個特定的稱為根的結點。 當\(N>1\)時,其餘結點可分為\(m(m>0)\)個互不相交的有限集合\(T_1,T_2,\ldots,T_
資料結構之樹和二叉樹
樹型結構是一類重要的非線性資料結構,樹是以分支關係定義的層次結構。 樹(Tree) 樹是n(n>=0)個結點的有限集。 在任意一棵非空樹中: (1)有且僅有一個特定的根結點(Root) (2)當n>1時,其餘節點可分為m(m>0)個互不相交的有限集
Java資料結構:前序和中序還原二叉樹
根據二叉樹前根中根遍歷出來的陣列還原二叉樹。 前根:ABDGCEFH 中跟:DGBAECHF 上程式碼: private BinaryNode<T> create(T[] prelist, T
資料結構7--樹和二叉樹初識
1.樹的基本概念 樹是一種重要的非線性結構,他是由n個節點組成的有限集合(n>0) n=0時,稱為空樹,樹的頂端節點稱為樹的根,其餘節點可分為若干個互不相交的子集,每個子集本身又是一棵樹,
資料結構——樹和二叉樹的基本概念
樹是一種非線性結構,是遞迴結構。 樹的基本術語: 樹結點:包含一個數據元素及若干指向子樹的分支; 孩子結點:結點的子樹的根稱為該結點的孩子; 雙親結點:B結點是A結點的孩子,則A結點是B結點的雙親; 兄弟結點:同一雙親的孩子結點; 堂兄結點:同一層上結點;
C語言 資料結構 樹和二叉樹
樹 1、樹:是n節點的有限集。樹是n(n=>0)個節點的有限集。 n=0時成為空樹。 在任意一顆非空樹中:(1)有且僅有一個稱為根的節點;(2)當n>0時,其餘節點可分為m(m>0)個互不相交的有限集T1、T2、T3、Tm,其中每個節點又是一棵樹,並且稱
《資料結構》實驗五:樹和二叉樹 實驗(實驗報告)
一.實驗目的 鞏固樹和二叉樹的相關知識,特別是二叉樹的相關內容。學會運用靈活應用。 1.回樹和二叉樹的邏輯結構和儲存方法,清楚掌握樹和二叉樹的遍歷操作。 2.學習樹的相關知識來解決實際問題。 3.進一步鞏固程式除錯方法。 4.進一步鞏固模板程式設計。
Javascript之資料結構與演算法的二叉樹和二叉搜尋樹實現
Javascript之資料結構與演算法的二叉樹和二叉搜尋樹實現 簡介 程式碼實現 簡介 二叉樹中的節點最多隻能有兩個子節點:一個是左側子節點,另一個是右側子節點。 二叉搜尋樹( BST)是二叉樹的一種,但是它只允許你在
資料結構-二叉樹和二叉查詢樹
先按樹-二叉樹-二叉查詢樹的順序解釋會比較清楚。 一,樹 樹(Tree)是n(n≥0)個結點的有限集。在任意一棵非空樹中: (1)有且僅有一個特定的被稱為根(Root)的結點; (2)當n>1時,其餘結點可分為m(m>0)個互不相交的有限集T1,T2,…,Tm,
淺談演算法和資料結構(7):二叉查詢樹
前文介紹了符號表的兩種實現,無序連結串列和有序陣列,無序連結串列在插入的時候具有較高的靈活性,而有序陣列在查詢時具有較高的效率,本文介紹的二叉查詢樹(Binary Search Tree,BST)這一資料結構綜合了以上兩種資料結構的優點。 二叉查詢樹具有很高的靈活性
資料結構:簡單算數表示式二叉樹的構建和求值
內容:編寫一個程式,先用二叉樹來表示一個簡單算術表示式,樹的每一個結點包括一個運算子或者運算數。在簡單算術表示式中只含+,-,*,/ 和一位正整數且格式正確(不包含括號),並且要先按照先乘除後加減的原則構造二叉樹,然後由對應的二叉樹計算該表示式的值。 解: 這裡用非遞迴演算