一、角點定義

有定義角點的幾段話：

1、角點檢測(Corner Detection)是計算機視覺系統中用來獲得影象特徵的一種方法，廣泛應用於運動檢測、影象匹配、視訊跟蹤、三維建模和目標識別等領域中。也稱為特徵點檢測。


角點通常被定義為兩條邊的交點，更嚴格的說，角點的區域性鄰域應該具有兩個不同區域的不同方向的邊界。而實際應用中，大多數所謂的角點檢測方法檢測的是擁有特定特徵的影象點，而不僅僅是“角點”。這些特徵點在影象中有具體的座標，並具有某些數學特徵，如區域性最大或最小灰度、某些梯度特徵等。


現有的角點檢測演算法並不是都十分的魯棒。很多方法都要求有大量的訓練集和冗餘資料來防止或減少錯誤特徵的出現。角點檢測方法的一個很重要的評價標準是其對多幅影象中相同或相似特徵的檢測能力，並且能夠應對光照變化、影象旋轉等影象變化。

2、在我們解決問題時，往往希望找到特徵點，“特徵”顧名思義，指能描述物體本質的東西，還有一種解釋就是這個特徵微小的變化都會對物體的某一屬性產生重大的影響。而角點就是這樣的特徵。


觀察日常生活中的“角落”就會發現，“角落”可以視為所有平面的交匯處，或者說是所有表面的發起處。假設我們要改變一個牆角的位置，那麼由它而出發的平面勢必都要有很大的變化。所以，這就引出了影象角點的定義


“如果某一點在任意方向的一個微小變動都會引起灰度很大的變化，那麼我們就把它稱之為角點”

3、

特徵檢測與匹配是Computer Vision 應用總重要的一部分，這需要尋找影象之間的特徵建立對應關係。點，也就是影象中的特殊位置，是很常用的一類特徵，點的區域性特徵也可以叫做“關鍵特徵點”(keypoint feature

)，或“興趣點”(interest point)，或“角點”(conrner)。

關於角點的具體描述可以有幾種：

• 一階導數(即灰度的梯度)的區域性最大所對應的畫素點；
• 兩條及兩條以上邊緣的交點；
• 影象中梯度值和梯度方向的變化速率都很高的點；
• 角點處的一階導數最大，二階導數為零，指示物體邊緣變化不連續的方向。

二、角點檢測演算法

1、Moravec角點檢測演算法

Moravec角點檢測演算法是最早的角點檢測演算法之一。該演算法將角點定義為具有低“自相關性”的點。演算法會檢測影象的每一個畫素，將畫素周邊的一個鄰域作為一個patch，並檢測這個patch和周圍其他patch的相關性。這種相關性通過兩個patch間的平方差之和(SSD)來衡量，SSD值越小則相似性越高。


如果畫素位於平滑影象區域內，周圍的patch都會非常相似。如果畫素在邊緣上，則周圍的patch在與邊緣正交的方向上會有很大差異，在與邊緣平行的方向上則較為相似。而如果畫素是各個方向上都有變化的特徵點，則周圍所有的patch都不會很相似。


Moravec會計算每個畫素patch和周圍patch的SSD最小值作為強度值，取區域性強度最大的點作為特徵點。

2、Harris角點檢測

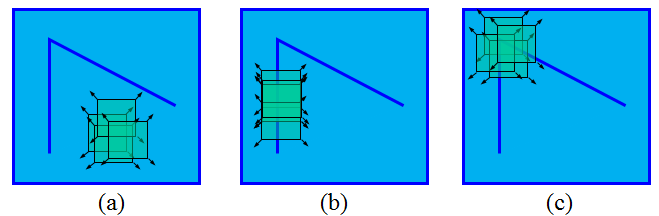
當一個視窗在影象上移動，在平滑區域如圖(a)，視窗在各個方向上沒有變化。在邊緣上如圖(b)，視窗在邊緣的方向上沒有變化。在角點處如圖(c)，視窗在各個方向上具有變化。Harris角點檢測正是利用了這個直觀的物理現象，通過視窗在各個方向上的變化程度，決定是否為角點。

將影象視窗平移[u,v]產生灰度變化E(u,v)

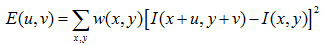
由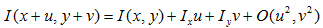：， 得到：

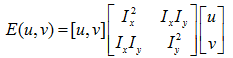
對於區域性微小的移動量 [u,v]，近似表達為：

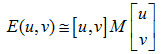
其中M是 2*2 矩陣，可由影象的導數求得：

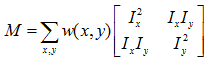
E(u,v)的橢圓形式如下圖：

定義角點響應函式 R 為：

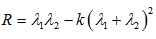
Harris角點檢測演算法就是對角點響應函式R進行閾值處理：R > threshold，即提取R的區域性極大值。

【相關程式碼】

OpenCV中定義了 cornerHarris 函式：

1. void cornerHarris( InputArray src, OutputArray dst, int blockSize,  
2.                                 int ksize, double k,  
3.                                 int borderType=BORDER_DEFAULT );  

可以結合 convertScaleAbs 函式，通過閾值取角點：

1. void cornerHarris_demo( int, void* )  
2. {  
3.   Mat dst, dst_norm;  
4.   dst = Mat::zeros( src.size(), CV_32FC1 );  
5.   /// Detector parameters
6.   int blockSize = 2;  
7.   int apertureSize = 3;  
8.   double k = 0.04;  
9.   /// Detecting corners
10.   cornerHarris( src_gray, dst, blockSize, apertureSize, k, BORDER_DEFAULT );  
11.   /// Normalizing
12.   normalize( dst, dst_norm, 0, 255, NORM_MINMAX, CV_32FC1, Mat() );  
13.   convertScaleAbs( dst_norm, dst_norm_scaled );   
14.   /// Drawing a circle around corners
15.   for( int j = 0; j < dst_norm.rows ; j++ )  
16.      { for( int i = 0; i < dst_norm.cols; i++ )  
17.           {  
18.             if( (int) dst_norm.at<float>(j,i) > thresh )  
19.               {   
20.                 circle( dst_norm_scaled, Point( i, j ), 5,  Scalar(0), 2, 8, 0 );   
21.                 circle(src,Point( i, j ), 5,  Scalar(255,0,0), -1, 8, 0 );  
22.               }  
23.           }   
24.      }      
25.   /// Showing the result
26.   imshow( corners_window, dst_norm_scaled );  
27.   imshow( source_window, src );    
28. }  

另一篇對Harris的講解（http://www.cnblogs.com/ztfei/archive/2012/05/07/2487123.html）

在我們解決問題時，往往希望找到特徵點，“特徵”顧名思義，指能描述物體本質的東西，還有一種解釋就是這個特徵微小的變化都會對物體的某一屬性產生重大的影響。而角點就是這樣的特徵。

觀察日常生活中的“角落”就會發現，“角落”可以視為所有平面的交匯處，或者說是所有表面的發起處。假設我們要改變一個牆角的位置，那麼由它而出發的平面勢必都要有很大的變化。所以，這就引出了影象角點的定義

“如果某一點在任意方向的一個微小變動都會引起灰度很大的變化，那麼我們就把它稱之為角點”

由上面定義，我們可以想到演算法思路：去檢測影象畫素的灰度變化情況，即求解　　

，其中，I(x,y)表示畫素的灰度值

對於上式，我們希望找到使E的值儘量大的點，則，將上式右邊泰勒展開得：

整理可得：

，進而可以表示為下式

這裡考慮進去窗函式，設

於是，Harris整理出Harris運算元的公式：

，其中M即為上面的矩陣，但是為什麼會有這個運算元呢，我試著給一點解釋。

讓我們來重新來考慮矩陣，一切的問題還得迴歸到數學上去

，這個矩陣先擺在這裡，我們先看一下協方差矩陣。

　　協方差矩陣的作用為什麼比方差和均值要大呢？顯而易見方差和均值只是一維隨機變數的統計值，而協方差就不一樣了，它可以表示多維隨機變數之間的相關性資訊。協方差矩陣的一個很出色的應用就是在PCA中，選擇主方向。協方差矩陣的對角線的元素表示的是各個維度的方差，而非對角線上的元素表示的是各個維度之間的相關性，因此，在PCA中，我們儘量將非對角線上的元素化為0，即將矩陣對角化，選特徵值較大的維度，去掉特徵值較小的維度，來獲得主方向，並且使主方向與其他方向的相關性儘量小。那現在看看這個矩陣M,通過上面對協方差的描述，我們完全可以把這個矩陣看做一個二維隨機分佈的協方差矩陣，那麼我們要做的就是將其對角化，求矩陣的兩個特徵值，然後根據這兩個特徵值來判斷是不是角點（兩個特徵值都大代表角點）。

而對於Harris運算元來說，我們也可以寫成下式的形式：

，單單從這個式子中我們無法與上面聯絡起來，上面是說要讓兩個特徵值都大的點，而這個式子是要求使R最大的點，而也沒有辦法一眼看出R與兩個特徵值之間的單調性關係。

下面我只是去驗證此式的正確性，至於它到底是根據什麼構造的，我還不清楚，如果有人知道，請告訴我一下~~

我們這裡設，進而可以設，所以,現在我們對求導，整理後可得下式：

，對於k值，我們一般取0.04~0.06，所以對於角點，導數是正的，且隨著特徵值的增大，導數呈上升的趨勢。也就是說這個運算元是符合上面的理論分析的。

像上面這樣去求解原則上是沒有問題的，可是，眾所周知，原始的Harris角點檢測演算法不具有尺度不變性（也就是說如果影象的尺度發生變化，那麼可能原來是角點的點在新的尺度就不是角點了）。

所以，我們在進行運算的開始先將影象轉化到尺度空間表示，即將原影象進行尺度變換，而尺度變換的方式就是問題的輸入訊號與尺度核函式做卷積運算：

，其中這裡的運算為卷積運算，不是乘運算。即

，其中sigma表示尺度。然後，我們就使用L代替原影象去進行運算，而尺度成了我們運算的引數了。

我們知道Harris角點本身就不受光照，旋轉的影響，現在我們又使其滿足尺度不變性，所以，Harris角點可以作為一個優秀的特徵來幫助我們解決問題。

本文只介紹了一下空域上的Harris角點的檢測，但是我們現在需要將Harris角點擴充套件到時空域中，其實道理都差不多，再續！

還有一段對Harris的計算步驟描述：

3、Shi-Tomasi 演算法

 

Shi-Tomasi 演算法是Harris 演算法的改進。Harris 演算法最原始的定義是將矩陣 M 的行列式值與 M 的跡相減，再將差值同預先給定的閾值進行比較。後來Shi 和Tomasi 提出改進的方法，若兩個特徵值中較小的一個大於最小閾值，則會得到強角點。

如上面第二幅圖中，對自相關矩陣 M 進行特徵值分析，產生兩個特徵值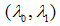和兩個特徵方向向量。因為較大的不確定度取決於較小的特徵值，也就是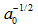，所以通過尋找最小特徵值的最大值來尋找好的特徵點也就解釋的通了。
Shi 和Tomasi 的方法比較充分，並且在很多情況下可以得到比使用Harris 演算法更好的結果。

【相關程式碼】

由於這種Shi-Tomasi運算元與1994年在文章 Good Features to Track [1]中提出，OpenCV 實現的演算法的函式名定義為 goodFeaturesToTrack：

1. void goodFeaturesToTrack( InputArray image, OutputArray corners,  
2.                                      int maxCorners, double qualityLevel, double minDistance,  
3.                                      InputArray mask=noArray(), int blockSize=3,  
4.                                      bool useHarrisDetector=false, double k=0.04 );  

自定義使用函式（以方便createTrackbar的響應）如下：

1. void cornerShiTomasi_demo( int, void* )  
2. {  
3.   if( maxCorners < 1 ) { maxCorners = 1; }  
4.   /// Parameters for Shi-Tomasi algorithm
5.   vector<Point2f> corners;  
6.   double qualityLevel = 0.01;  
7.   double minDistance = 10;  
8.   int blockSize = 3;  
9.   bool useHarrisDetector = false;  
10.   double k = 0.04;  
11.   /// Copy the source image
12.   Mat cormat;  
13.   /// Apply corner detection :Determines strong corners on an image.
14.   goodFeaturesToTrack( src_gray,   
15.                corners,  
16.                maxCorners,  
17.                qualityLevel,  
18.                minDistance,  
19.                Mat(),  
20.                blockSize,  
21.                useHarrisDetector,  
22.                k );  
23.   /// Draw corners detected
24.   for( int i = 0; i < corners.size(); i++ ){   
25.       circle( dst_norm_scaled,  corners[i], 5,  Scalar(255), 2, 8, 0 );   
26.       circle( src, corners[i], 4, Scalar(0,255,0), 2, 8, 0 );   
27.   }  
28.   /// Show what you got
29.   imshow( corners_window, dst_norm_scaled );  
30.   imshow( source_window, src );    
31. }  

實踐

在主函式中定義兩個進度條方便調整閾值：

1. namedWindow( source_window, CV_WINDOW_AUTOSIZE );  
2. createTrackbar( "Threshold: ", source_window, &thresh, max_thresh, cornerHarris_demo );  
3. createTrackbar( "Max  corners:", source_window, &maxCorners, maxTrackbar, cornerShiTomasi_demo );    
4. namedWindow( corners_window, CV_WINDOW_AUTOSIZE );  
5. namedWindow( source_window, CV_WINDOW_AUTOSIZE );  
6. imshow( source_window, src );    
7. cornerHarris_demo( 0, 0 );  
8. cornerShiTomasi_demo( 0, 0 );  

這裡還需要說的是OpenCV 2.4.2中給的角點檢測跟蹤的示例程式碼有些問題，是應為SURF等不再定義在 feature2d模組中，而是legacy和nonfree，所以需要加入引用：

1. #include "opencv2/legacy/legacy.hpp"
2. #include "opencv2/nonfree/nonfree.hpp"

角點檢測結果：

藍色實心點為Harris檢測結果，綠色空心圈為goodFeaturetoTrack檢測結果。

M特徵值分解後每個畫素點相減的圖（也就是Harris閾值判斷的圖）如下：

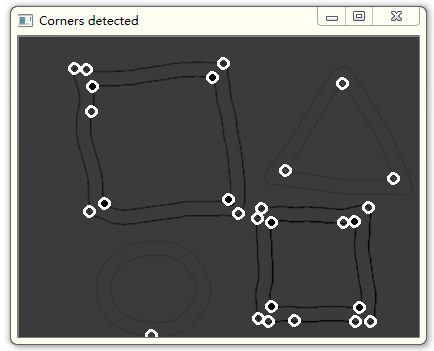
黑色實心點為Harris閾值檢測結果，白色空心圈為閾值為27時Shi-Tomasi檢測結果。

4、FAST角點檢測演算法

Smith 和 Brady在1997年提出了一種完全不同的角點提取方法，即“SUSAN (Smallest UnivalueSegment AssimilatingNucleus)”提取運算元。SUSAN 提取運算元的基本原理是，與每一影象點相關的區域性區域具有相同的亮度。如果某一視窗區域內的每一像元亮度值與該視窗中心的像元亮度值相同或相似，這一視窗區域將被稱之為“USAN”。計算影象每一像元的“USAN”，為我們提供了是否有邊緣的方法。位於邊緣上的像元的“USAN”較小，位於角點上的像元的“USAN”更小。因此，我們僅需尋找最小的“USAN”，就可確定角點。該方法由於不需要計算影象灰度差，因此，具有很強的抗噪聲的能力。


Edward Rosten and TomDrummond 在2006年提出了一種簡單快速的角點探測演算法，該演算法檢測的角點定義為在畫素點的周圍鄰域內有足夠多的畫素點與該點處於不同的區域。應用到灰度影象中，即有足夠多的畫素點的灰度值大於該點的灰度值或者小於該點的灰度值。


考慮下圖中p點附近半徑為3的圓環上的16個點，一個思路是若其中有連續的12個點的灰度值與p點的灰度值差別超過某一閾值，則可以認為p點為角點。

這一思路可以使用機器學習的方法進行加速。對同一類影象，例如同一場景的影象，可以在16個方向上進行訓練，得到一棵決策樹，從而在判定某一畫素點是否為角點時，不再需要對所有方向進行檢測，而只需要按照決策樹指定的方向進行2-3次判定即可確定該點是否為角點。