角點檢測:Harris角點及Shi-Tomasi角點檢測
角點
特徵檢測與匹配是Computer Vision 應用總重要的一部分,這需要尋找影象之間的特徵建立對應關係。點,也就是影象中的特殊位置,是很常用的一類特徵,點的區域性特徵也可以叫做“關鍵特徵點”(keypoint feature),或“興趣點”(interest point),或“角點”(conrner)。
關於角點的具體描述可以有幾種:
- 一階導數(即灰度的梯度)的區域性最大所對應的畫素點;
- 兩條及兩條以上邊緣的交點;
- 影象中梯度值和梯度方向的變化速率都很高的點;
- 角點處的一階導數最大,二階導數為零,指示物體邊緣變化不連續的方向。
Harris角點檢測
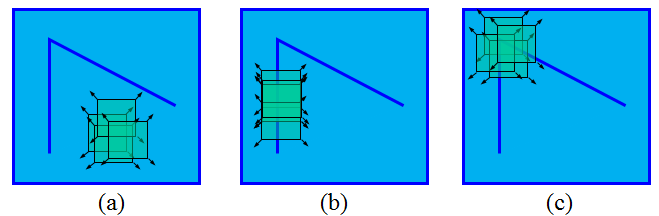
當一個視窗在影象上移動,在平滑區域如圖(a),視窗在各個方向上沒有變化。在邊緣上如圖(b),視窗在邊緣的方向上沒有變化。在角點處如圖(c),視窗在各個方向上具有變化。Harris角點檢測正是利用了這個直觀的物理現象,通過視窗在各個方向上的變化程度,決定是否為角點。
將影象視窗平移[u,v]產生灰度變化E(u,v)
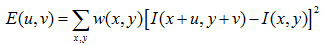
由: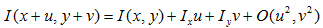 , 得到:
, 得到:
對於區域性微小的移動量 [u,v],近似表達為:
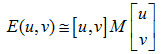
其中M是 2*2 矩陣,可由影象的導數求得:
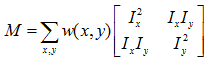
E(u,v)的橢圓形式如下圖:

定義角點響應函式 R 為:
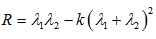
Harris角點檢測演算法就是對角點響應函式R進行閾值處理:R > threshold,即提取R的區域性極大值。
【相關程式碼】
OpenCV中定義了 cornerHarris 函式:
-
void cornerHarris( InputArray src, OutputArray dst, int blockSize,
- int ksize, double k,
- int borderType=BORDER_DEFAULT );
可以結合 convertScaleAbs 函式,通過閾值取角點:
- void cornerHarris_demo( int, void* )
- {
- Mat dst, dst_norm;
- dst = Mat::zeros( src.size(), CV_32FC1 );
- /// Detector parameters
-
intblockSize = 2;
- int apertureSize = 3;
- double k = 0.04;
- /// Detecting corners
- cornerHarris( src_gray, dst, blockSize, apertureSize, k, BORDER_DEFAULT );
- /// Normalizing
- normalize( dst, dst_norm, 0, 255, NORM_MINMAX, CV_32FC1, Mat() );
- convertScaleAbs( dst_norm, dst_norm_scaled );
- /// Drawing a circle around corners
- for( int j = 0; j < dst_norm.rows ; j++ )
- { for( int i = 0; i < dst_norm.cols; i++ )
- {
- if( (int) dst_norm.at<float>(j,i) > thresh )
- {
- circle( dst_norm_scaled, Point( i, j ), 5, Scalar(0), 2, 8, 0 );
- circle(src,Point( i, j ), 5, Scalar(255,0,0), -1, 8, 0 );
- }
- }
- }
- /// Showing the result
- imshow( corners_window, dst_norm_scaled );
- imshow( source_window, src );
- }
Shi-Tomasi 演算法
Shi-Tomasi 演算法是Harris 演算法的改進。Harris 演算法最原始的定義是將矩陣 M 的行列式值與 M 的跡相減,再將差值同預先給定的閾值進行比較。後來Shi 和Tomasi 提出改進的方法,若兩個特徵值中較小的一個大於最小閾值,則會得到強角點。
如上面第二幅圖中,對自相關矩陣 M 進行特徵值分析,產生兩個特徵值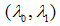 和兩個特徵方向向量。因為較大的不確定度取決於較小的特徵值,也就是
和兩個特徵方向向量。因為較大的不確定度取決於較小的特徵值,也就是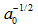 ,所以通過尋找最小特徵值的最大值來尋找好的特徵點也就解釋的通了。
,所以通過尋找最小特徵值的最大值來尋找好的特徵點也就解釋的通了。
Shi 和Tomasi 的方法比較充分,並且在很多情況下可以得到比使用Harris 演算法更好的結果。
【相關程式碼】
由於這種Shi-Tomasi運算元與1994年在文章 Good Features to Track [1]中提出,OpenCV 實現的演算法的函式名定義為 goodFeaturesToTrack:
- void goodFeaturesToTrack( InputArray image, OutputArray corners,
- int maxCorners, double qualityLevel, double minDistance,
- InputArray mask=noArray(), int blockSize=3,
- bool useHarrisDetector=false, double k=0.04 );
自定義使用函式(以方便createTrackbar的響應)如下:
- void cornerShiTomasi_demo( int, void* )
- {
- if( maxCorners < 1 ) { maxCorners = 1; }
- /// Parameters for Shi-Tomasi algorithm
- vector<Point2f> corners;
- double qualityLevel = 0.01;
- double minDistance = 10;
- int blockSize = 3;
- bool useHarrisDetector = false;
- double k = 0.04;
- /// Copy the source image
- Mat cormat;
- /// Apply corner detection :Determines strong corners on an image.
- goodFeaturesToTrack( src_gray,
- corners,
- maxCorners,
- qualityLevel,
- minDistance,
- Mat(),
- blockSize,
- useHarrisDetector,
- k );
- /// Draw corners detected
- for( int i = 0; i < corners.size(); i++ ){
- circle( dst_norm_scaled, corners[i], 5, Scalar(255), 2, 8, 0 );
- circle( src, corners[i], 4, Scalar(0,255,0), 2, 8, 0 );
- }
- /// Show what you got
- imshow( corners_window, dst_norm_scaled );
- imshow( source_window, src );
- }
實踐
在主函式中定義兩個進度條方便調整閾值:
- namedWindow( source_window, CV_WINDOW_AUTOSIZE );
- createTrackbar( "Threshold: ", source_window, &thresh, max_thresh, cornerHarris_demo );
- createTrackbar( "Max corners:", source_window, &maxCorners, maxTrackbar, cornerShiTomasi_demo );
- namedWindow( corners_window, CV_WINDOW_AUTOSIZE );
- namedWindow( source_window, CV_WINDOW_AUTOSIZE );
- imshow( source_window, src );
- cornerHarris_demo( 0, 0 );
- cornerShiTomasi_demo( 0, 0 );
這裡還需要說的是OpenCV 2.4.2中給的角點檢測跟蹤的示例程式碼有些問題,是應為SURF等不再定義在 feature2d模組中,而是legacy和nonfree,所以需要加入引用:
- #include "opencv2/legacy/legacy.hpp"
- #include "opencv2/nonfree/nonfree.hpp"
角點檢測結果:

藍色實心點為Harris檢測結果,綠色空心圈為goodFeaturetoTrack檢測結果。
M特徵值分解後每個畫素點相減的圖(也就是Harris閾值判斷的圖)如下:
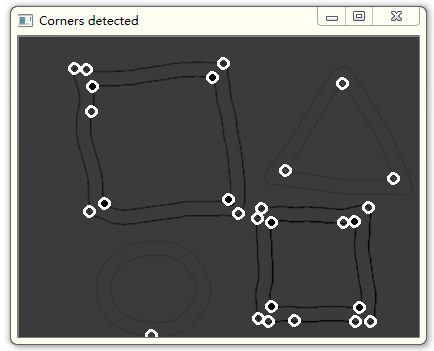
黑色實心點為Harris閾值檢測結果,白色空心圈為閾值為27時Shi-Tomasi檢測結果。
參考資料:
[1] Shi and C. Tomasi. Good Features to Track. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 593-600, June 1994.
[2] Richard Szeliski. Computer Vision: Algorithms and Applications. Springer, New York, 2010.
